常见排序算法

最新推荐文章于 2025-12-04 16:25:00 发布

原创最新推荐文章于 2025-12-04 16:25:00 发布 · 439 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#c语言 #数据结构 #排序算法

今天咱们一起聊聊几种排序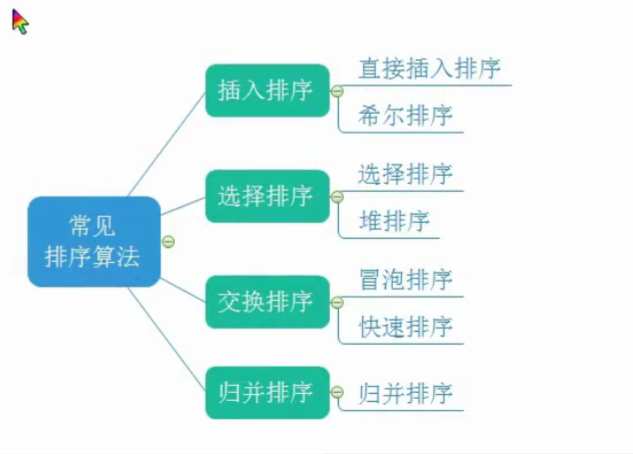

这是四种常见的排序方式，插入排序，选择排序，交换排序和归并排序，其中，我觉得归并排序较为困难一点。

我将按照上述顺序，依次进行演示。

直接插入排序：

上面是插入排序的相关代码

他是将当前的数据，不断往前（前面儿已经有序）比较向前插入，一边比较一边移动，如果当前数据＜目标数据，那就把目标数据直接复制后移，所以现在最后面儿两个就是目标数据，依次类推，知道找到当前数据＞目标数据，那就赋值啦，兄弟

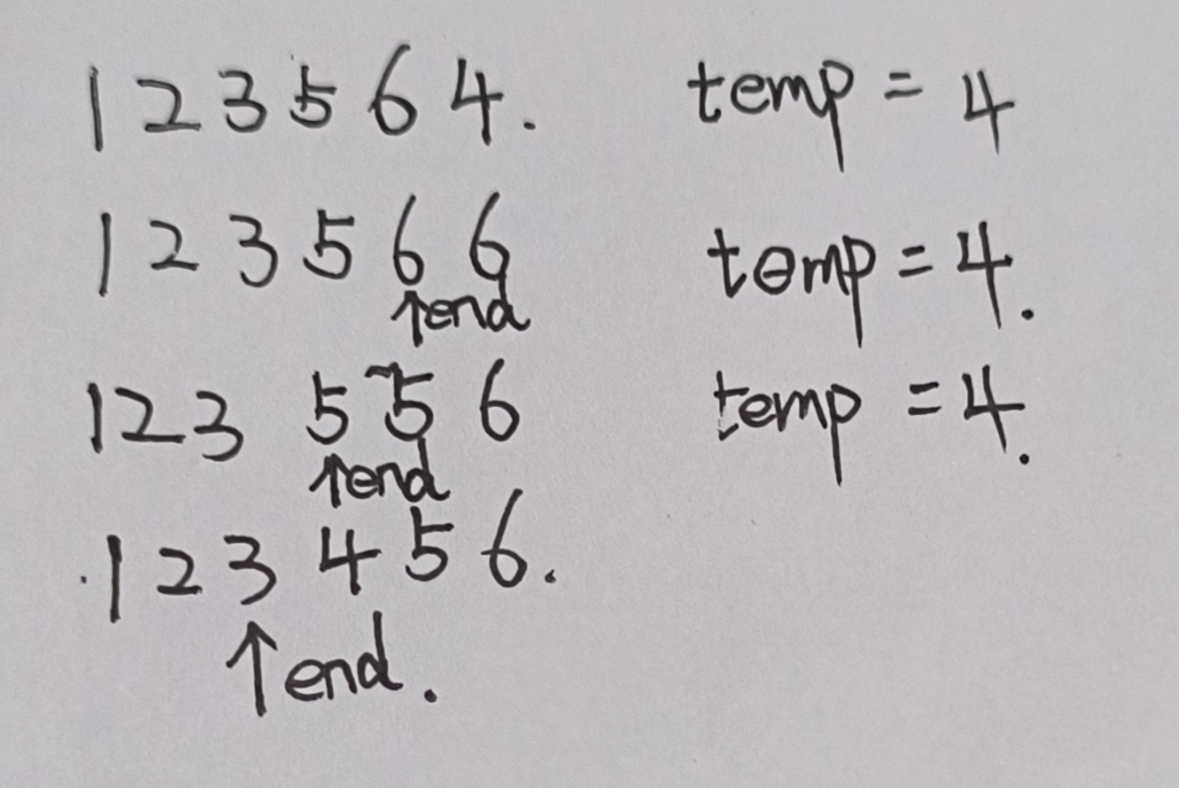
for循环中i为什么开始＝1，不等于0呢，因为第一个数，只有一个数的话，他肯定是有序的，所以不需要管呢

那他的稳定性如何呢，（稳定性就是同样大小的数据，在排序前后的相对位置是否变化，变化则不稳定），因为他大于那个数，才往后移，那么等于的时候也就没移动呢，所以是稳定滴昂。

想想直接插入，他的复杂度是多少呢？如果他本来就是有序的，那么他就只需要和前一个比较，就结束了这次循环，有n个数据，实际比较n-1次，所以此时最好情况的时间复杂度是O（n），那么最坏情况嘞，就是你要排成1.2.3.4.5.6.7.结果他是7.6.5.4.3.2.1，此时久麻烦啦，基本你每次都得走n次，所以最坏的时间复杂度是O（n²）。那么如何改进这种算法呢？我还是一前一后比嘛，那要是刚好是逆置的呢，那么最后一个数跳的太慢了，我咋才能让他快速跳到前面儿呢？

希尔排序：

这个是希尔排序，其实和插入排序是类似的，相当于是插入排序的pro max版本哈，这次我设置了一个gap，也就是间隔，唉～我不一次一个一个来了，我现在直接跳gap个，然后gap÷＝2，最后等于1的时候，不就是直接插入排序嘛，而且还是经过前面儿调整过的，这时候已经接近有序了昂，此刻的直接插入排序效率就想当高了。

那他的稳定性怎么样呢？这是要注意了昂！因为他是跳组进行的，所以，不稳定！！！

复杂度方面呢，这个经过之前大佬的研究，平均复杂度差不多在O（n的1.3次方）。

选择排序：

选择排序比较简单，我这个是两端都开始呢，左边儿最小，右边儿最大，同时走，也能相对快一点儿，先都把最左边儿的定义为最小和最大，然后遍历数组，比较值，不断更替最小数的角标，最后交换，但是！注意！这有一个坑。如果你最小值的角标本来是最大值，然后你交换了之后，那么最大值位置也就改变了昂！此刻就得调整一下了

那怎么调整呢？思考一下9的角标是谁嘞？是不是min嘞，然后把min赋值给max不就行啦，解决问题～

他的稳定性怎么样呢？是不是不稳定的嘞，此如5.5.3，就会颠倒相对位置呢，所以是不稳定的呢！

那复杂度嘞，这个算法就比较一般了，因为你每次都得遍历数组，去找最大最小，所以他的平均复杂度是O（n²）。

堆排序：

先来说说他的核心，就是向下调整算法，这个排序比较厉害昂，具体可见我之前发的，二叉树的基本操作，有超级详细的保姆级别讲解，甚至还赠送向上调整昂

那么他稳定吗？很明显，不稳定的嘛。

那时间复杂度嘞，这个比较厉害了哈，调整的最坏最好复杂度是log以2为底的n，（log2 N），但是前面儿还有个建堆哇，是n，所以结合起来就是nlog2 n。

冒泡排序：

冒泡排序比较简单昂，无非就是一前一后比较，然后大滴放后面儿，小的在前面儿，重点有一个，第二个for循环中，j＜n-i-1，这是为什么呢？因为经过n次后，是不是就剩n-i个数据需要排了，然后角标是不是应该-1，因为最大角标是个数-1嘛，所以～

然后还有一个，就是，你这一趟下去，如果一次都没交换，那么他是不是就已经有序了呢，你想一想，所以设置一个变量，记录有没有交换，没交换，直接就结束～

那他稳定性怎么样呢，他是一个稳定排序呢，只有他小于才会交换，大于就不会交换呢，总体复杂度是O（n²）。

来喽来喽，他真的来喽

快速排序：

他目前有三种比较多的核心写法：

第一种，左右指针法：

这是第一种，他其实就是从左边儿开始找一个比目标数据大的数，再直接从右边儿找，找比目标数据小的数，然后两个再交换（注意交换的是数本身！不是角标昂），然后继续找，依次类推，直到左角标等于右角标，甚至右角标小于左角标，再跳出循环，交换目标数据和当前角标的正确值，最终返回目标数据的角标，他就在最终应该呆的地方啦，然后从左边儿，右边儿，依次递归，最终排序成功

第二种，挖坑填数法：

这个算法是先保存最左边儿的数，然后他就想当于是一个空白，因为你保存了这个数呢，然后从右边儿开始找一个比这个数小的数，放在那个空白处，这下空白处就刷新了，右边儿就出现了一个空白处，再从左边儿找，找一个大于目标数的数，再放在右空白处，以此类推，最后的空白处，放目标数，这样他就在应该的位置上啦。最后依次递归左边儿和右边儿，就完成排序啦。

但是这两种，都很有可能在极端情况下，复杂度直逼O(n²)因此有了最后一种相当高效的算法，前后指针法

第三种前后指针法：