二叉树的最大深度（leetcode）

难度：简单

题目描述

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

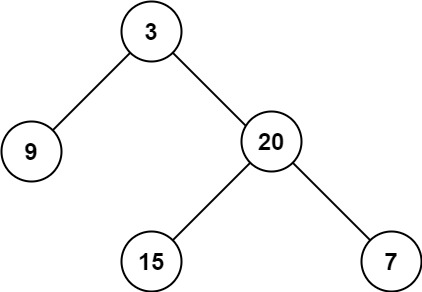
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

思路

先递归再回溯。例如对示例1：

递归：

root=3：计算左子树深度maxDepth（9）

              计算右子树深度maxDepth（20）

              取max（左深度，右深度）+1

root=9：计算左子树深度maxDepth（nullptr）=0

              计算右子树深度maxDepth（nullptr）=0

              取max（0,0）+1=1，即节点9深度为1

root=20：计算左子树深度maxDepth（15）

              计算右子树深度maxDepth（7）

              取max（左深度，右深度）+1

root=15：计算左子树深度maxDepth（nullptr）=0

              计算右子树深度maxDepth（nullptr）=0

              取max（0,0）+1=1，故节点15深度为1

root=7：计算左子树深度maxDepth（nullptr）=0

              计算右子树深度maxDepth（nullptr）=0

              取max（0,0）+1=1，即节点7深度为1

回溯：

节点20的深度：max（1,1）+1=2

节点3的深度：max（1,2）+1=3

    

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root==nullptr) return 0;
        return max(maxDepth(root->left),maxDepth(root->right))+1;
    }
};

复杂度

• 时间复杂度：O(n)。n为二叉树节点个数。

• 空间复杂度：O(h)。h为二叉树深度，递归需要栈空间，而栈空间取决于递归的深度。