BCE（二元交叉熵）与Dice

注：作者为初学者，有些知识不太熟悉，可能描述有误，望见谅。

BCE

        二元交叉熵（Binary Cross-Entropy, BCE）是深度学习中用于二分类任务的损失函数，衡量模型预测概率与真实标签之间的差异。适用于输出为概率值（如Sigmoid激活后的结果）的场景，例如图像分类中的正/负样本判断。

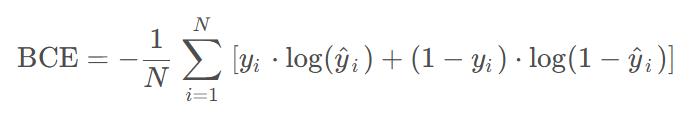
        PyTorch提供了BCELoss和BCEWithLogitsLoss两种实现方式。

代码示例：

（1）BCELoss要求输入已经经过sigmoid激活函数（输出在0到1之间）：

import torch
import torch.nn as nn

# 假设预测值和真实标签的shape均为 [batch_size]
bce_loss = nn.BCELoss()
output = torch.sigmoid(model(input))  # 需手动sigmoid
loss = bce_loss(output, target)

 （2）BCEWithLogitsLoss结合了sigmoid和BCE，数值稳定性更好（推荐使用这种）：

bce_logits_loss = nn.BCEWithLogitsLoss()
output = model(input)  # 无需手动sigmoid
loss = bce_logits_loss(output, target)

注：与网络中的激活函数不冲突，BCEWithLogitsLoss 只关心最后一层有没有额外加 sigmoid。

适用场景：

（1）语义分割

        二分类：血管、视网膜、皮肤病变、道路、缺陷检测等几乎默认先上 BCE(+Dice)。

        多分类：先做成 One-vs-Rest 再用 BCE（等价于多标签交叉熵），例如同时分割“肿瘤+水肿+坏死”。

（2）边缘检测 / 轮廓预测

        HED、RCF、DexiNed 等系列网络输出边缘概率图，损失就是逐像素 BCE（有时给正边缘像素加高权重）。

（3）生成式模型

        GAN 里的判别器、VAE 的重建项（像素灰度归一化到 0–1 后）常用 BCE，最早 DCGAN 就这么干。

Dice

        Dice系数（Dice Coefficient）是一种用于衡量集合相似度的指标，广泛应用于图像分割、医学影像分析等领域。其定义为两个集合交集大小的两倍除以两个集合大小的和。Dice系数的取值范围在0到1之间，数值越大表示相似度越高。

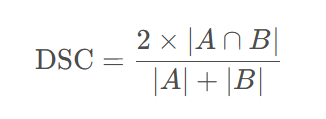
        Dice系数在图像分割任务中常被用作评估模型性能的指标，尤其是在医学影像分割中。它可以衡量预测分割结果与真实标签之间的重叠程度，帮助评估模型的准确性。

代码示例：

        模拟了一个二值分割任务的预测结果和标签，展示了如何计算Dice系数和Dice损失。

import torch
import torch.nn as nn

def dice_coefficient(pred, target, smooth=1e-6):
    """
    计算Dice系数
    :param pred: 预测的分割结果（经过sigmoid或softmax）
    :param target: 真实的分割标签（0或1）
    :param smooth: 平滑系数，避免除以零
    :return: Dice系数
    """
    intersection = (pred * target).sum()
    union = pred.sum() + target.sum()
    dice = (2. * intersection + smooth) / (union + smooth)
    return dice

class DiceLoss(nn.Module):
    """
    Dice损失函数
    """
    def __init__(self, smooth=1e-6):
        super(DiceLoss, self).__init__()
        self.smooth = smooth

    def forward(self, pred, target):
        dice = dice_coefficient(pred, target, self.smooth)
        return 1 - dice  # 返回Dice损失

# 示例用法
if __name__ == "__main__":
    # 模拟预测结果和真实标签
    pred = torch.sigmoid(torch.randn(1, 1, 256, 256))  # 假设预测结果经过sigmoid
    target = torch.randint(0, 2, (1, 1, 256, 256)).float()  # 二值标签

    # 计算Dice系数和Dice损失
    dice_score = dice_coefficient(pred, target)
    dice_loss = DiceLoss()(pred, target)

    print(f"Dice Coefficient: {dice_score.item():.4f}")
    print(f"Dice Loss: {dice_loss.item():.4f}")

代码解释：

        dice_coefficient函数接收预测结果和真实标签，计算两者的交集和并集，最终返回Dice系数。平滑系数smooth用于避免分母为零的情况。

        DiceLoss类继承自nn.Module，将Dice系数转换为损失值（1 - Dice系数），便于模型优化。

        可能的疑问点：把 Dice 系数变成 1 − Dice 只是为了“把越大越好的指标变成越小越好的损失”，与梯度下降法的方向保持一致。

        PyTorch 默认的 optimizer.step() 是沿负梯度方向更新参数，也就是“让损失变小”。Dice 系数最大为 1（完美重叠），最小为 0（毫无重叠），越大越好。因此取 1 − Dice 后，完美时损失=0，最差时损失≈1，越小越好，正好符合优化器的“下山”方向。

BCE与Dice结合使用

        医学影像分割任务中常使用二元交叉熵（BCE）与Dice Loss结合的方式，主要由于两者互补的特性。

        BCE Loss逐像素计算分类误差，对类别不平衡敏感，能保证像素级分类精度；Dice Loss直接优化分割区域的重叠度，对目标区域大小变化鲁棒，但可能忽视像素级细节。结合两者可平衡局部和全局优化目标。

代码示例（pytorch）：

import torch
import torch.nn as nn
import torch.nn.functional as F

class BCEDiceLoss(nn.Module):
    def __init__(self, weight_bce=0.5, weight_dice=0.5, smooth=1e-5):
        super(BCEDiceLoss, self).__init__()
        self.weight_bce = weight_bce
        self.weight_dice = weight_dice
        self.smooth = smooth


    def forward(self, pred, target):
        # BCE Loss计算
        bce_loss = F.binary_cross_entropy_with_logits(pred, target)

        # Dice Loss计算
        pred = torch.sigmoid(pred)
        intersection = (pred * target).sum()
        union = pred.sum() + target.sum()
        dice_loss = 1 - (2. * intersection + self.smooth) / (union + self.smooth)

        # 加权结合
        total_loss = self.weight_bce * bce_loss + self.weight_dice * dice_loss
        return total_loss
 

代码参数解释：

（1）初始化：

        weight_bce：控制 BCE 损失的权重，默认 0.5。

        weight_dice：控制 Dice 损失的权重，默认 0.5。

        smooth：平滑系数，用于防止 Dice 系数计算时分母为零，默认 1e-5。

（2）forward：

        pred：模型输出的预测值（未经 sigmoid 激活）。

        target：真实标签（一般为 0 或 1）。