背包问题之01背包——以洛谷P1048 [NOIP2005 普及组] 采药为例

 引言

今天呢，我们来学一下背包问题中最为简单的01背包。大家学了这么长时间的编程，都知道0代表false为假，1代表true为真，故此01背包也就指代的是每种物品有且只有一个，对于每个物品只需要考虑选与不选两种情况的最简单易懂的背包问题。

我们接下来就以洛谷的P1048 [NOIP2005 普及组] 采药为例给大家讲解一下01背包问题我们是如何解决的👇

题目描述

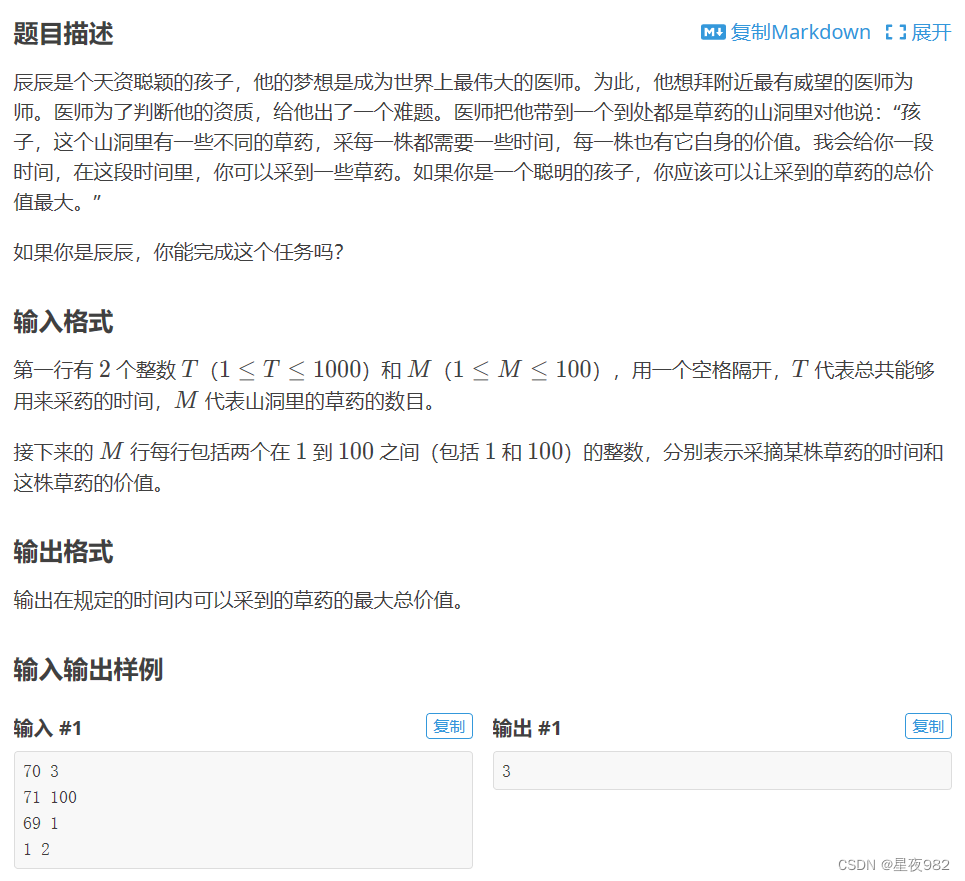
分析

这个题目就是最经典的01背包，透过题目所给的生活背景我们来看这道题目，就是题目会输入两个数，分别代表采药的总时间(此处等价于背包的容量)和山洞里草药的总数目，接下来的M行所代表的就是采摘这株草药所需的时间(等价于草药所占的空间)和它的价值。

那我们来跳出这道题目来看，其实就是有固定容积的背包，要选取合适的物品，使得背包中的物品总价值达到最大。

由于这道题目的背包容量和草药的情况的都不确定，为了更好的讲解01背包的解题思路，我们通过下面的这个例子来让大家了解一下这类问题的解题思路是怎样的。

01背包举例

有一个小偷要偷东西，他所背的包只能容纳体积为8的物品，而摆在他面前的物品有四样，它们所占背包的容积和其价值分别如下表所示👇

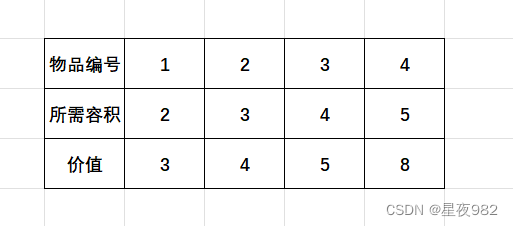
那么看完了这四件物品，相信大家也能很快地得出答案——12！偷取第二件物品和第四件物品就可以了。但是这个具体应该偷第几件物品又是如何的出来的呢？

我们在这里先定义一个新的运算为f(m,n)，他所代表的意义就是当小偷面前有m件物品，而他的背包还能容纳体积为n的物体之时能够偷取东西的最大价值，比如这道题目的f(4,8)=12。

那么接下来我们来探究一下f(4,8)=12是如何算出来的。首先当小偷面前有4件物品的时候，对于第四件物品，小偷有两种选择——偷或不偷。如果偷的话，那么f(4,8)=f(3,3)+8，进行过一次选择，那么刚刚的第四件物品就已经过去了，那么需要小偷继续选择的物品就只剩下了前三件，故此m由4变成了3，而由于偷取了第四件物品，那么小偷所偷东西的总价值就应该加上第四件物品的价值——8，与此同时，小偷背包的剩余容量n也要由最初的8减去第四件物品所占的空间——5，所以我们就得到了f(4,8)=f(3,3)+8这样一个式子；至于如果小偷正在面对第四件物品的时候 良心发现  选择不偷的话，f(4,8)=f(3,8)，这很好理解，尽管小偷没偷第四件物品，但由于进行过一次选择，故此m会减一，但是总价值和小偷背包的剩余容量都是不会改变的。

 这就是对小偷面对第4件物品可能做出的两种选择的模拟，那么我们继续往下看还会出现什么样的情况呢。

当我们顺着f(3,3)+8继续往下走的时候，我们会发现小偷在面对第三件物品的时候好像只有一条路可以走了，那就是不偷，因为第三件物品所需的空间为4，然而此时小偷背包只剩下了3的空间，故此小偷只有一种不偷的选择可供选择了，此时f(4,8)=f(3,3)+8=f(2,3)+8。

由于篇幅的限制，我就不把每种情况都一一赘述了，直接上咱们的流程图👇

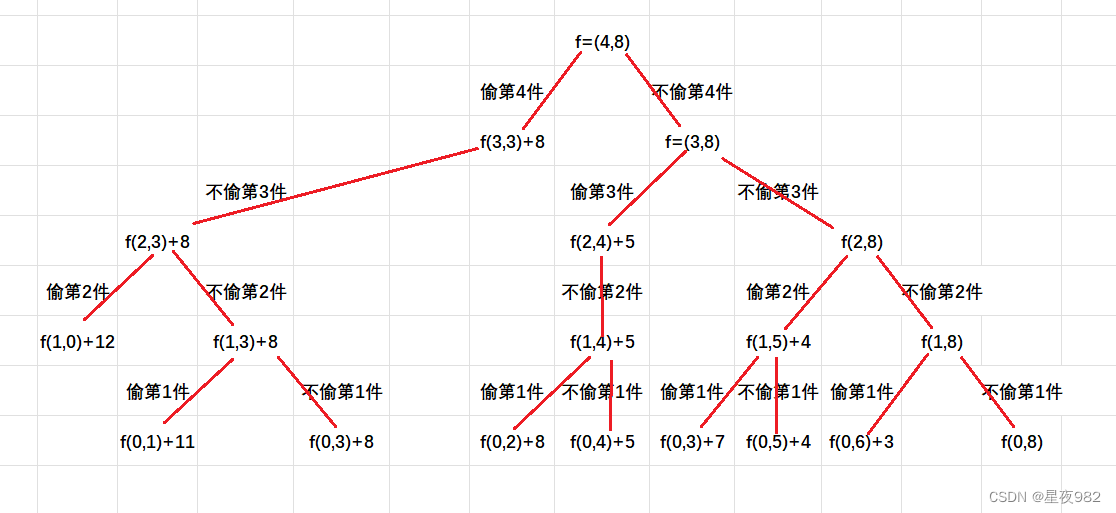
最后我们会发现，分支图最后一个分支的f(m,n)中m、n至少有一个为0，这是为什么呢？其实很好理解：m为0就是将所有的物品都遍历了一次，所有的物品都进行过一次选择了，这时候就没有物品再供小偷进行选取了；而n为0则是小偷背包已满 ，再装不下任何东西了，这也会导致我们没有办法继续向下进行，故此所有的分支都在含0的地方停止。同时，很好理解的是，根据我们之前对于f(m,n)的定义，只要m或者n为0，那么f(m,n)的值也就为0了。

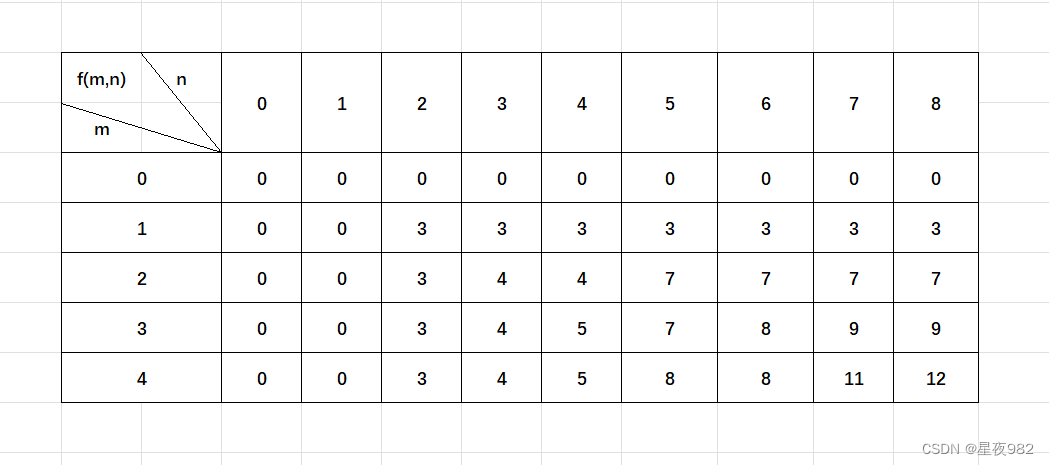
故此，我们打出了以下的表格👇

#include <bits/stdc++.h>
using namespace std;
int main()
{
	int f[5][9]={0};        //二维数组充当表格
	int q[5]={0,3,4,5,8};        //存放价值
	int v[5]={0,2,3,4,5};        //存放体积
	int i,j;
	for(i=1;i<5;i++){
		for(j=1;j<9;j++){
			if(q[i]>j)
			f[i][j]=f[i-1][j];        //体积过大装不下
			else
			f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+q[i]);
		}
	}
	return 0;
}

这就是这道01背包最经典的题目的解法，接下来咱们看看洛谷的这道题目应该怎么做👇

这道题目其实也是一样的，我们只需要对输进来的数进行存放就可以了。

所以我们来放一下我们的AC代码👇

C++代码

#include <bits/stdc++.h> 
using namespace std;
int v[105],q[105];        //分别存放体积和价值
int f[105][1005];        //进行打表
int main()
{
    int n,m;
    cin >> n >> m ;
    for(int i=1;i<=m;i++)
    {
        cin >> v[i] >> q[i] ;        //进行对应的存放
    }
    for(int i=1;i<=m;i++) 
        for(int j=n;j>=0;j--)  
        {
            if(j>=v[i])
            f[i][j]=max(f[i-1][j-v[i]]+q[i],f[i-1][j]); 
            else
            f[i][j]=f[i-1][j];         //等同于刚刚的模板
        }
    cout << f[m][n] ;    //输出所要的答案
    return 0;
}

优化

其实我们在看着之前的状态转移方程就会发现，我们后面的数据都是由前面的数据变化所得到的，比如两个物品的数据都是由一个物品的数据和对第二个物品选或不选的判断结合所得到的，故此，我们可以可以用滚动数组对之前的代码进行优化，也就是只用一维数组来解决咱们的01背包问题。

 

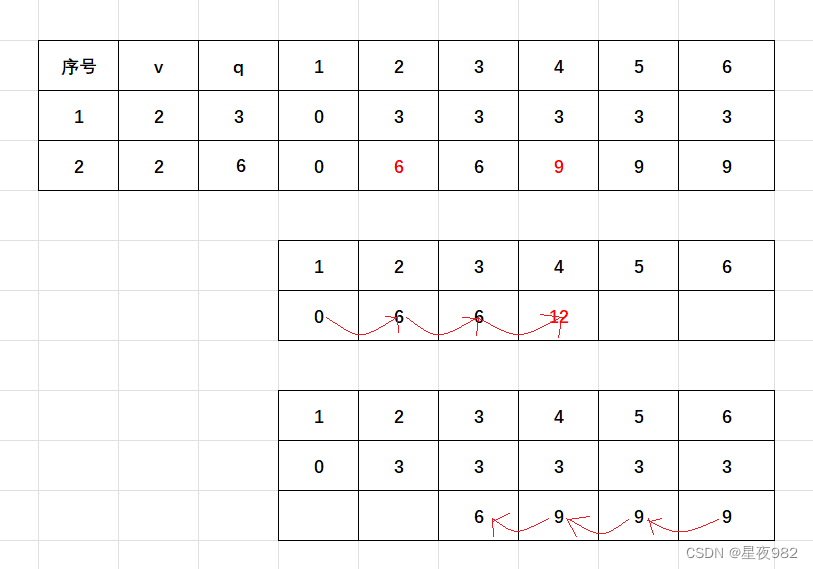
比如这种情况：有两个物品， 他们的体积均为2，但是价值分别为3和6，我们的背包总容积为6，此时我们的f[][]还没有什么问题，但是当我们只用一维数组的时候，在第二次数组滚动的时候出现了问题，在背包容量为4的时候我们发现我的数值变成了12，这很明显是不对的，这是为什么呢？是因为我们在计算背包容量为4的时候使用了背包容量为2的值，本来我们应该使用的是f[][]上一行里面背包容量为2的值，这里面的那个值已经被更新成了6，之前的3已经不复存在了，故此我们就会出错，所以，为了使上一行背包容量小的数值不被过早地更新，我们在滚动数组的时候要进行倒序滚动，以这种方式将上一行背包容量小的数值保留下来！

C++代码

#include<iostream>
using namespace std;
int t,m;
int v[110],q[110];
int f[1010];
int main()
{
	int i,j;
	cin>>t>>m;
	for(i=1;i<=m;i++)
	cin>>v[i]>>q[i];
	for(i=1;i<=m;i++)
		for(j=t;j>=v[i];j--)        //滚动更新要倒序进行
			if(f[j-v[i]]+q[i]>f[j])
			f[j]=f[j-v[i]]+q[i];
	cout<<f[t];
	return 0;
}

好啦这就是01背包的两种解法，希望对大家能有所帮助，谢谢大家的阅读~~