在机器学习领域,我们都盼着预测结果能精准无误。一开始,简单的决策树帮我们开了个好头,效果还算差强人意。紧接着,随机森林和 AdaBoost 横空出世,预测表现更上一层楼。然而,梯度提升的出现,彻底改写了游戏规则,让预测精度实现了质的飞跃。
有人说:“梯度提升算法之所以效果拔群,背后的原理其实挺简单:它会接连构建一个又一个模型,每一个新模型都一门心思去修正前面所有模型犯下的错误。这种循序渐进纠错的方式,就是它的独特魅力所在。” 起初,我真以为就这么简单,可每次查阅梯度提升算法资料,试图搞懂它的运行机制时,扑面而来的都是密密麻麻、晦涩难懂的数学公式,还有那些让人摸不着头脑的图表,看得我一头雾水,心里直冒火。不信你也去试试,感受肯定跟我一样。
咱别再这么折腾了,换个真正好理解的方式来剖析它。接下来,我们将直观地梳理梯度提升在训练过程中的各个步骤,重点聚焦回归案例。回归场景可比分类简单多了,这样能避开那些繁杂恼人的数学运算。就好比多级火箭为了顺利进入轨道,会逐步抛掉多余的负重,我们也将一步步消除预测过程中产生的误差。

定义
梯度提升是一种很厉害的集成机器学习技术。它的运作方式是搭建一连串的决策树,这些决策树可不是各自为政,而是有着紧密的协作关系。每一棵新生成的决策树,都肩负着修正前面决策树所犯错误的重任。这里得提一下,它和AdaBoost有所不同,AdaBoost倾向于使用浅树,而梯度提升选用的弱学习器是更深的树。 在进行回归任务时,梯度提升会按顺序一棵一棵地添加树。每一棵新树在训练时,主要目标是最小化残差误差,也就是实际值与预测值之间的差距,而不是像普通模型那样直接从原始目标数据中学习。最终的预测结果,是把所有树的输出结果累加起来得到的。 梯度提升模型最大的优势,就在于它的加性学习过程。虽说每棵树只聚焦于修正集合里还残留的错误,但当这些树按顺序组合起来,就会形成一个超强大的预测器。它通过持续关注模型中那些还没解决好的问题部分,一步步地降低整体的预测误差,让预测结果越来越精准。

小tips: 梯度提升 (Gradient Boosting) 属于提升 (Boosting) 算法家族,因为它会按顺序构建树,每棵新树都会尝试纠正其前几棵的错误。然而,与其他提升 (Boosting) 方法不同,梯度提升 (Gradient Boosting) 从优化的角度来解决问题。
使用的数据集
在本文中,我们将以经典的高尔夫数据集作为回归分析的示例。虽然梯度提升可以有效地处理回归和分类任务,但在本文中将专注于更简单的任务,在本例中是回归——根据天气状况预测将参加高尔夫比赛的球员人数。

列:“阴天(独热编码为 3 列)”、“温度”(华氏度)、“湿度”(百分比)、“有风”(是/否)和“玩家人数”(目标特征)
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
# Create dataset
dataset_dict = {
'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast',
'sunny', 'sunny', 'rain', 'sunny', 'overcast', 'overcast', 'rain',
'sunny', 'overcast', 'rain', 'sunny', 'sunny', 'rain', 'overcast',
'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
'Temp.': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0,
72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0,
88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
'Humid.': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0,
90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0,
65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
'Wind': [False, True, False, False, False, True, True, False, False, False, True,
True, False, True, True, False, False, True, False, True, True, False,
True, False, False, True, False, False],
'Num_Players': [52, 39, 43, 37, 28, 19, 43, 47, 56, 33, 49, 23, 42, 13, 33, 29,
25, 51, 41, 14, 34, 29, 49, 36, 57, 21, 23, 41]
}
# Prepare data
df = pd.DataFrame(dataset_dict)
df = pd.get_dummies(df, columns=['Outlook'], prefix='', prefix_sep='')
df['Wind'] = df['Wind'].astype(int)
# Split features and target
X, y = df.drop('Num_Players', axis=1), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
主要机制
梯度提升的工作原理如下:
- Initialize Model: 从一个简单的预测开始,往往是目标值的平均值。
- Iterative Learning: 对于一定次数的迭代,计算残差,训练决策树来预测这些残差,并将新树的预测(按学习率缩放)添加到累计总数中。
- Build Trees on Residuals: 每棵新树都关注所有先前迭代中剩余的错误。
- Final Prediction: 将所有树贡献(按学习率缩放)和初始预测相加。

小tips: 梯度提升回归器是从平均预测开始,并通过多棵树对其进行改进,每棵树都会以小步骤修复前几棵树的错误,直到达到最终预测。
训练步骤
将遵循标准梯度提升方法:
1.0. 设置模型参数:
在构建任何树之前,我们需要设置控制学习过程的核心参数:
· 要连续构建的树的数量(通常为 100 棵,该案例为了演示因此选择了 50 棵),
· 学习率(通常为 0.1)
· 每棵树的最大深度(通常为 3)

小tips: 该树状图显示了我们的关键设置:每棵树有 3 个级别,我们将以 0.1 的小步前进创建 50 个级别。
对于第一棵树
2.0 对标签进行初始预测。一般来说是平均值(就像虚拟预测(dummy prediction)一样)。
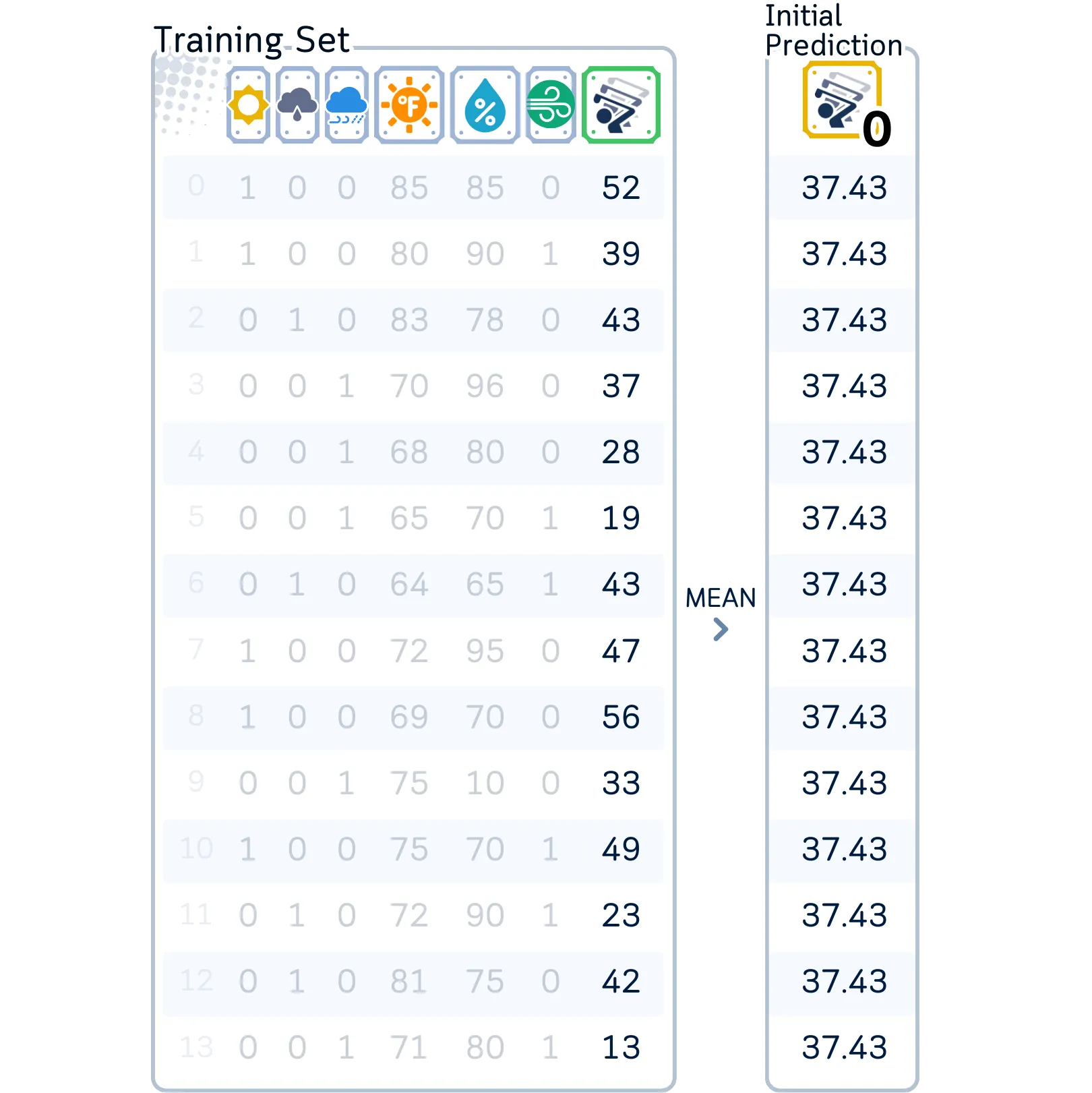
为了开始预测,我在这使用所有训练数据的平均值(37.43)作为每种情况的第一个猜测。
2.1.计算暂时残差(伪残差):
残差 = 实际值 — 预测值(residual = actual value — predicted value)

小tips: 通过从训练集中的每个目标值中减去平均预测值(37.43)来计算初始残差。
2.2. 构建一棵决策树来预测这些残差。决策树的构建步骤与回归树完全相同。

小tips: 第一棵决策树通过在我们的特征中搜索模式来开始训练,这些模式可以最好地预测我们初始平均预测的计算残差。
a. 计算根节点的初始 MSE(均方误差)

小tips: 就像在常规回归树中一样,我们计算均方误差(MSE),但这次我们测量的是残差的分布(实际上是围绕零),而不是实际值(实际上是围绕它们的平均值)。
b. 对于每个特征:
· 按特征值对数据进行排序

小tips: 对于数据集中的每个特征,我们对其值进行排序并在它们之间找到潜在的分割点,就像在标准决策树中一样,以确定划分残差的最佳方法。
· 对于每个可能的分割点:
·· 将样本分为左右两组
·· 计算两组的均方误差 (MSE)
·· 计算本次分割的均方误差 (MSE) 减少量

小tips: 与常规回归树类似,我们通过计算两个组的加权 MSE 来评估每个分割,但在这里我们测量的是分割组相似残差而不是相似目标值的程度。
c. 选择能够最大程度减少 MSE 的分割


上图可以看到该树使用值为 0.5 的“雨”特征进行第一次分割,根据残差将样本分成两组——这个第一个决策将通过更深层次的额外分割进行细化。
d. 继续分裂直至达到最大深度或每片叶子的最小样本量。

从上图可以看出经过对不同特征进行三级分割后,我们的第一棵树创建了八个不同的组,每个组对残差都有自己的预测。
2.3 计算叶子值
对于每片叶子,求出残差的平均值。

我们第一棵树中的每片叶子都包含该组中残差的平均值——这些值将用于调整和改进我们最初的平均预测值 37.43。
2.4. 更新预测
· 对于训练数据集中的每个数据点,根据新树确定其属于哪个叶子节点。

上图展示了通过第一棵树运行我们的训练数据,每个样本根据天气特征遵循自己的路径来获得其预测残差值,这将有助于纠正我们最初的预测。

上图展示出我们的模型通过小步骤更新其预测:它将每个预测残差的 10%(我们的学习率为 0.1)添加到我们最初的预测 37.43 中,从而略微改善预测。
对于第二棵树
2.1. 根据当前模型计算新的残差
a. 计算目标预测值与当前预测值的差值。
这些残差与第一次迭代的残差略有不同。

在使用第一棵树更新我们的预测之后,我们计算新的残差——注意它们比原始残差略小,表明我们的预测正在逐渐改善。
2.2. 构建一棵新树来预测这些残差。过程与第一棵树相同,但目标是新的残差。

从图中可以看到,现在我们开始构建第二棵树,目的是预测新出现的、数值更小的残差。构建这棵树时,采用的是和之前构建第一棵树相同的流程。但此刻,我们的关注点变成了找出并弥补第一棵树在预测过程中遗漏的那些错误。
2.3. 计算每片叶子的平均残差

第二棵树在结构上和第一棵树如出一辙,它们都依据相同的天气特征来构建,就连分裂点的设置也完全一样。不过,第二棵树叶子节点的值明显更小。这意味着什么呢?这表明它正专注于对第一棵树预测后仍残留的错误进行精细调整,努力让预测结果更加精准 。
2.4. 更新模型预测
· 将新树的预测结果乘以学习率。然后将新缩放的树预测结果添加到累计总数中。

在将数据输入第二棵树进行处理后,我们再次以0.1的学习率迈出微小的步伐来更新预测值。随后,计算得出的新残差比之前的更小了——这说明我们的模型正在逐步学习数据中的规律。
对于第三棵树
重复步骤 2.1-2.3 进行剩余迭代。注意,每棵树的残差不同。
· 树会逐渐关注难以预测的模式
· 学习率通过限制每棵树的贡献来防止过拟合

当我们构建更多的树时,需要注意分割点如何缓慢移动,叶子中的残差值如何变小——到第 50 棵树时,与第一棵树相比,我们使用不同的特征组合进行了微小的调整。
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
# Train the model
clf = GradientBoostingRegressor(criterion='squared_error', learning_rate=0.1, random_state=42)
clf.fit(X_train, y_train)
# Plot trees 1, 2, 49, and 50
plt.figure(figsize=(11, 20), dpi=300)
for i, tree_idx in enumerate([0, 2, 24, 49]):
plt.subplot(4, 1, i+1)
plot_tree(clf.estimators_[tree_idx,0],
feature_names=X_train.columns,
impurity=False,
filled=True,
rounded=True,
precision=2,
fontsize=12)
plt.title(f'Tree {tree_idx + 1}')
plt.suptitle('Decision Trees from GradientBoosting', fontsize=16)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show() 
scikit-learn 的可视化展示了我们的梯度提升树是如何演化的:从树 1 进行具有较大预测值的大分裂,到树 50 进行具有微小调整的精细分裂 —— 每棵树都纠正了先前树中剩余的错误。
测试步骤
用于预测:
a. 从初始预测(平均玩家人数)开始
b. 将输入通过每棵树运行,以获得其预测调整值
c. 根据学习率缩放每棵树的预测值。
d. 将所有这些调整值加到初始预测值上
e. 求和后直接得出预测的玩家人数

在对未见数据进行预测时,每棵树都会贡献自己的小预测,从树 1 中的 5.57 开始到树 50 中的 0.008——所有这些预测都按我们的 0.1 学习率进行缩放,并添加到我们的基本预测 37.43 以获得最终答案。
评估步骤
构建完所有树后,我们可以评估测试集。

可以看出我们的梯度提升模型实现了 4.785 的 RMSE,比单个回归树的 5.27 有了很大的改进——这表明结合许多小的修正可以比一棵复杂的树产生更好的预测!
# Get predictions
y_pred = clf.predict(X_test)
# Create DataFrame with actual and predicted values
results_df = pd.DataFrame({
'Actual': y_test,
'Predicted': y_pred
})
print(results_df) # Display results DataFrame
# Calculate and display RMSE
from sklearn.metrics import root_mean_squared_error
rmse = root_mean_squared_error(y_test, y_pred)
print(f"\nModel Accuracy: {rmse:.4f}")关键参数
以下是梯度提升的关键参数,尤其是在scikit-learn:
n_estimators:要使用的树的数量(通常为 100-1000)。当学习率较低时,使用更多树通常可以提高性能。
learning_rate:也称为“收缩”,用于缩放每棵树的贡献(通常为 0.01-0.1)。较小的值需要更多的树,但通常可以通过使学习过程更细粒度来获得更好的结果。
subsample:用于训练每棵树的样本比例(通常为 0.5-0.8)。此可选功能增加了随机性,可以提高鲁棒性并减少过度拟合。
这些参数协同工作:较小的学习率需要更多的树,而更深的树可能需要较小的学习率以避免过度拟合。
与 AdaBoost 的主要区别
AdaBoost 和 Gradient Boosting 都是 boosting 算法,但它们从错误中学习的方式不同。以下是它们的主要区别:
max_depth在 Gradient Boosting 中通常较高(3-8),而 AdaBoost 更喜欢 stumps。- 没有
sample_weight更新,因为梯度提升使用残差而不是样本加权。 learning_rate与 AdaBoost 的较大值(0.1-1.0)相比,通常要小得多(0.01-0.1)。- 初始预测从平均值开始,而 AdaBoost 从零开始。
- 树是通过简单的加法而不是加权投票来组合的,这使得每棵树的贡献更加直接。
- 可选
subsample参数添加随机性,这是标准 AdaBoost 中不存在的功能。
优点和缺点
优点:
- 逐步修复错误:在梯度提升中,每棵新树都会专注于纠正先前树所犯的错误。这使得模型能够更好地改进其在先前错误领域的预测。
- 灵活的误差测量:与 AdaBoost 不同,梯度提升可以优化不同类型的误差测量(例如平均绝对误差、均方误差等)。这使得它能够适应各种类型的问题。
- 高精度:通过使用更详细的树并仔细控制学习率,梯度提升通常比其他算法提供更准确的结果,尤其是对于结构良好的数据。
缺点:
- 过拟合风险:使用更深的树和顺序构建过程可能会导致模型与训练数据的拟合度过高,从而降低其在新数据上的性能。这需要仔细调整树的深度、学习率和树的数量。
- 训练过程缓慢:与 AdaBoost 类似,树必须逐一构建,与可以并行构建树的算法(如随机森林)相比,训练速度较慢。每棵树都依赖于先前树的错误。
- 高内存使用率:需要更深、更多的树,这意味着梯度提升会比 AdaBoost 等更简单的提升方法消耗更多的内存。
- 对设置敏感:梯度提升的有效性很大程度上取决于找到学习率、树深度和树数量的正确组合,这可能比调整更简单的算法更复杂、更耗时。
结语
梯度提升 (Gradient Boosting) 是提升算法的一项重大改进。这一成功催生了 XGBoost 和 LightGBM 等热门版本,它们在机器学习竞赛和实际应用中得到了广泛的应用。
虽然梯度提升算法比简单的算法需要更仔细的调整——尤其是在调整决策树的深度、学习率和树的数量时——但它非常灵活且强大。这使得它成为解决结构化数据问题的首选。
梯度提升可以处理像 AdaBoost 这样的简单方法可能无法处理的复杂关系。它的持续流行和持续改进表明,使用梯度和逐步构建模型的方法在现代机器学习中仍然非常重要。
🌟 梯度提升回归器代码总结
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
from sklearn.ensemble import GradientBoostingRegressor
# Create dataset
dataset_dict = {
'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast',
'sunny', 'sunny', 'rain', 'sunny', 'overcast', 'overcast', 'rain',
'sunny', 'overcast', 'rain', 'sunny', 'sunny', 'rain', 'overcast',
'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
'Temp.': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0,
72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0,
88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
'Humid.': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0,
90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0,
65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
'Wind': [False, True, False, False, False, True, True, False, False, False, True,
True, False, True, True, False, False, True, False, True, True, False,
True, False, False, True, False, False],
'Num_Players': [52, 39, 43, 37, 28, 19, 43, 47, 56, 33, 49, 23, 42, 13, 33, 29,
25, 51, 41, 14, 34, 29, 49, 36, 57, 21, 23, 41]
}
# Prepare data
df = pd.DataFrame(dataset_dict)
df = pd.get_dummies(df, columns=['Outlook'], prefix='', prefix_sep='')
df['Wind'] = df['Wind'].astype(int)
# Split features and target
X, y = df.drop('Num_Players', axis=1), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
# Train Gradient Boosting
gb = GradientBoostingRegressor(
n_estimators=50, # Number of boosting stages (trees)
learning_rate=0.1, # Shrinks the contribution of each tree
max_depth=3, # Depth of each tree
subsample=0.8, # Fraction of samples used for each tree
random_state=42
)
gb.fit(X_train, y_train)
# Predict and evaluate
y_pred = gb.predict(X_test)
rmse = root_mean_squared_error(y_test, y_pred))
print(f"Root Mean Squared Error: {rmse:.2f}")power by Samy Baladram in TDS Archive





























 1305
1305

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










