一.顺序存储
用一维数组来存储二叉树,第i个结点就储存在arr[i]中
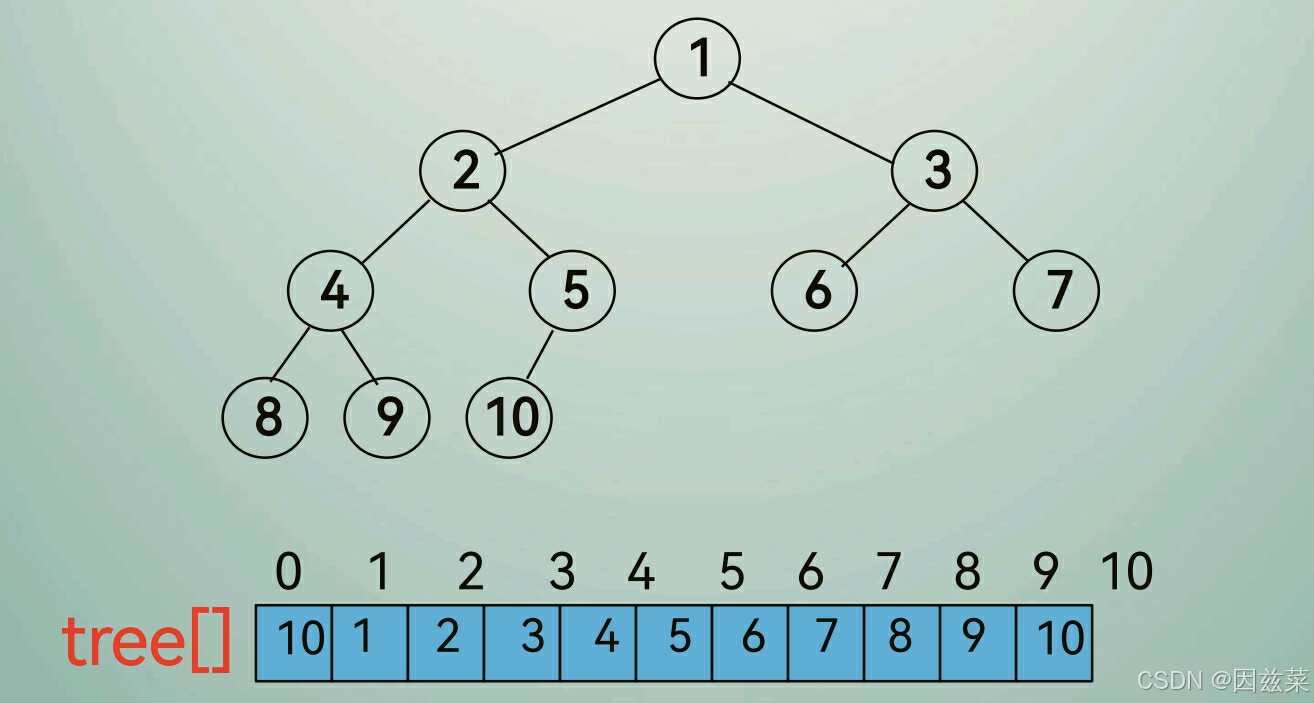
但是显然会有一个问题,如果这是一颗非完全二叉树,那要怎么办呢?
补充虚拟结点使其成为完全二叉树

观察层号,每层结点数,会发现:
(1)下一层的结点数总是上一层结点数的两倍;
(2)第i层的结点数为,而每层的结点编号初始值为
,而编号结束值为
-1
以下为用顺序结构创建二叉树和遍历的代码:
//假设这颗二叉树真实结点数为sum
void createBiTree(int sum) {
int tree[100];
int m = 0;//用于记录已经输入的结点数
int n = 1;//用于记录每层结点的起始值
int data;//用于记录结点的数据
int i;
while (m < sum) {
for ( i = n; i < 2*n - 1; i++) {
scanf_s("%d", &data);
tree[i] = data;
if (data != 0)m++;
}
n = n * 2;
}
tree[0] = i - 1;
}
void traverse(int*tree) {
int i = 1, j = 1;
while (i <= tree[0]) {
for (j = i; j <= 2 * i - 1; j++) {
if (tree[j] == 0)
printf("0");
else printf("%d", tree[j]);
}
printf("\n");
i = 2 * i;
}
}
二.链式存储
二叉链表
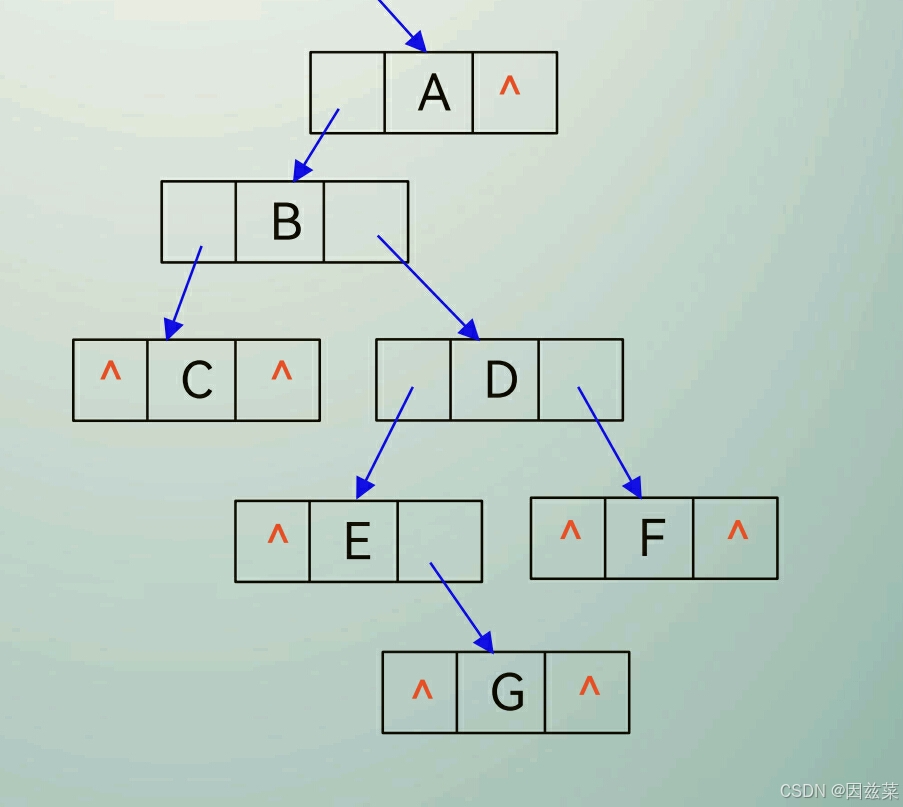
存储特点
1.非空指针数 = 边数 = 结点数-1 (n-1)
2.空指针个数 = 总指针个数-空指针个数 = 2n-(n-1) = n+1
创建结点
要用链式存储自然会先想到如何设计一个结点
二叉树的一个结点可以同时有一个左孩子和一个右孩子,则每个结点都需要储存其左右孩子的地址;
typedef struct node {
int data;
struct node* left;
struct node* right;
}node;
三叉链表
二叉链表存在的一个问题就是 从孩子结点回不到父母结点
所以可以在结点中再存储一个父母结点的地址,就变成了三叉链表
三.二叉树的操作
1.二叉树的遍历
主要分为三种遍历方式: 先根遍历,中根遍历和后根遍历
先根遍历
即先访问树根,再去访问左孩子和右孩子
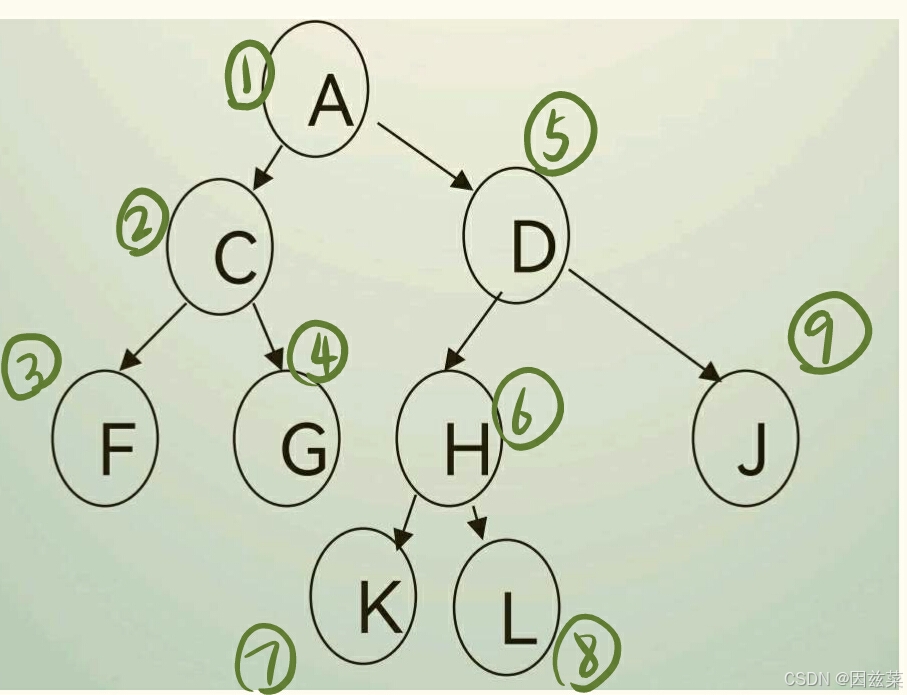
递归算法
void preOrder(node* tree) {
if (tree != NULL) {
printf("%d", tree->data);
preOrder(tree->left);
preOrder(tree->right);
}
}
非递归算法
如果不用递归的话,要注意到二叉链表是不能从孩子回到父母的,所以我们需要在遍历每一个结点的时候,把右孩子的地址储存起来,便于再次访问。这里就会用到栈
算法思想:
用一个指针去遍历结点;
(1)访问当前结点
(2)如果当前结点的右孩子不为空,则将其地址存入栈中
(3)指针继续访问当前结点的左孩子;
(4)如果左孩子为空,则弹栈,访问栈中地址所属的结点;
(5)当栈空,指针为空时循环结束
void pre_orderTraversal(treeNode* root) {
treeNode* p = root;
sqStack sq;
initStack(&sq);
while (p != NULL || sq.top != 0) {
if (p != NULL) {
printf("%d\n", p->value);
if(p->right!=NULL)
push(&sq, p->right);
p = p->left;
}
else{
treeNode* address = NULL;
pop(&sq, &address);
p = address;
}
}
}
中根遍历
中根遍历的访问顺序: 左孩子->根->右孩子
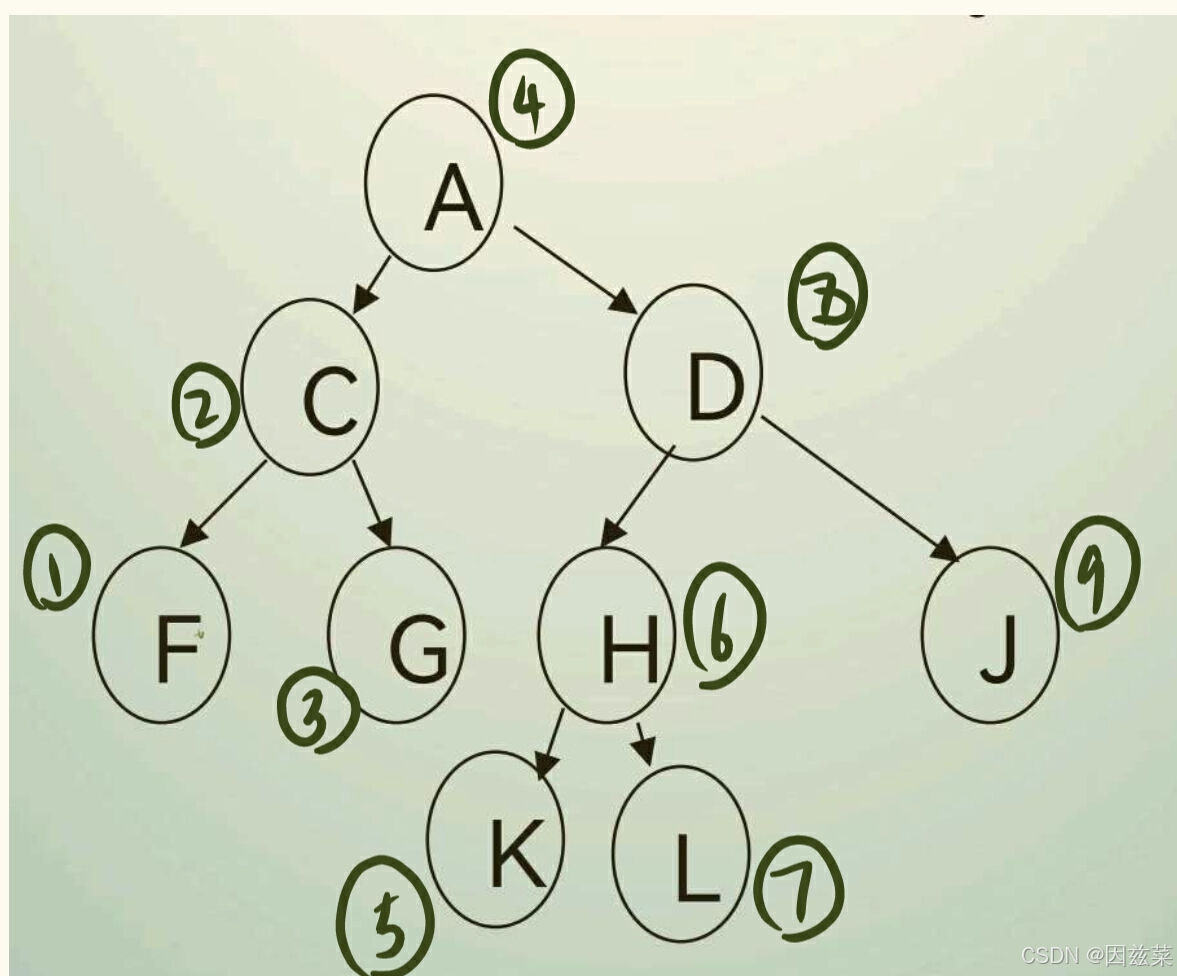
递归算法
和先根遍历是差不多的,就是把访问元素放在了语句的中间,非常简单
void inOrder(node* tree) {
if (tree != NULL) {
inOrder(tree->left);
printf("%d", tree->data);
inOrder(tree->right);
}
}
非递归算法
算法思想:
(1)将当前结点地址存入栈
(2)访问左孩子,一直到左下结点;
(3)当指针为空时,弹栈;
(4)访问元素;
(5)访问右孩子。
void in_orderTraversal(treeNode* root) {
treeNode* p = root;
sqStack sq;
initStack(&sq);
while (p != NULL || sq.top != 0) {
if (p != NULL) {
push(&sq, p);
p = p->left;
}
else{
pop(&sq, &p);
printf("%d\n", p->value); //这里要注意一定先要把元素取出来再进行访问
p = p->right;
}
}
}
后根遍历
后根遍历的访问顺序为左孩子->右孩子->根
递归算法
void inOrder(node* tree) {
if (tree != NULL) {
inOrder(tree->left);
inOrder(tree->right);
printf("%d", tree->data);
}
}
非递归算法的两种方式(难点)
1.后序遍历的非递归算法会比之前的要复杂一些
算法思想:
1.从根结点开始往左下角遍历,将遍历到的结点存入栈中;
2.指针为空时,查看其栈顶元素,如果其右孩子为空或者已经遍历过了,则访问栈顶元素;否则进入右子树;(这里要注意访问栈顶元素后一定要更新lastVisited并且将p置为空)
// 后序遍历
void post_orderTraversal(treeNode* root) {
if (root == NULL) return;
sqStack sq;
initStack(&sq);
treeNode* p = root;
treeNode* lastVisited = NULL;
while (p != NULL || sq.top != 0) {
// 先走到左子树的最深处
if (p != NULL) {
push(&sq, p);
p = p->left;
}
else {
treeNode* peekNode = sq.base[sq.top - 1]; // 查看栈顶元素
// 如果右子树为空,或者右子树已经被访问过
if (peekNode->right == NULL || peekNode->right == lastVisited) {
// 访问节点
pop(&sq, &p);
printf("%d\n", p->value);
lastVisited = p; // 更新lastVisited
p = NULL; // 设置p为NULL,防止下次循环处理已经访问的节点
}
else {
// 否则进入右子树
p = peekNode->right;
}
}
}
}
2.另外,还可以借助两个栈来实现
算法思想:
我们希望遍历的顺序是左->右->根
栈可以实现顺序的逆转 则只要入栈顺序为 根->右->左 出栈就是后序遍历的顺序了
栈 1 (
stack1):用于模拟递归中的节点访问。我们将树的根节点压入stack1。栈 2 (
stack2):用于存储节点的反向访问顺序。当节点从stack1弹出时,先将它压入stack2,这个栈保存的顺序是 根 -> 右 -> 左,因此我们可以通过弹出stack2中的节点来得到 左 -> 右 -> 根 的顺序,从而实现后序遍历。
//用两个栈进行后序遍历
void post_orderTraversal(treeNode* root) {
sqStack stack1;
sqStack stack2;
initStack(&stack1);
initStack(&stack2);
treeNode* p = root;
push(&stack1, root);
while (stack1.top!= 0) {
treeNode* node;
pop(&stack1, &node);
push(&stack2, node);
if (node->left) {
push(&stack1, node->left);
}
if (node->right) {
push(&stack1, node->right);
}
}
while (stack2.top!=0) {
treeNode* node;
pop(&stack2,&node);
printf("%d ", node->value);
}
}
2.计算叶子结点,计算度为2的结点
int countLeaf(treeNode* root) {
int n, n1, n2;
if (root == NULL)return 0;
else if (root->left == NULL && root->right == NULL)
return 1;
else {
n1 = countLeaf(root->left);
n2 = countLeaf(root->right);
n = n1 + n2;
return n;
}
}
//计算度为2的结点
int countDegree2(treeNode* root) {
if (root == NULL) return 0; // 空树不算度为 2 的节点
// 先递归左右子树,再判断当前节点是否是度为 2 的节点
int count = 0;
if (root->left != NULL && root->right != NULL) {
count = 1; // 当前节点有两个子节点,度为 2
}
// 递归左子树和右子树
return count + countDegree2(root->left) + countDegree2(root->right);
}
3.计算树的深度
int countDepth(treeNode* root) {
if (root == NULL) return 0;
else {
int leftDepth, rightDepth;
leftDepth = countDepth(root->left);
rightDepth = countDepth(root->right);
return 1 + ((leftDepth > rightDepth) ? leftDepth : rightDepth);
}
}
4.克隆树和交换树根
treeNode* clone(treeNode* root) {
treeNode* newRoot;
if (root == NULL) return NULL;
else {
newRoot = (treeNode*)malloc(sizeof(treeNode));
newRoot->value = root->value;
newRoot->left = clone(root->left);
newRoot->right = clone(root->right);
}
return newRoot;
}
这可以用于交换左右子树根
treeNode*swap(treeNode* root) {
treeNode* newRoot;
if (!root) return 0;
else {
newRoot = (treeNode*)malloc(sizeof(treeNode));
newRoot->left = clone(root->right);
newRoot->right = clone(root->left);
return newRoot;
}
}
四.由遍历序列确定唯一二叉树
由普通序列确定唯一二叉树
1.思考:给出一个字符串序列,是否能够根据序列创建出一棵二叉链表?
比如: ABCD
显然是不能的
如果这是一棵完全二叉树呢?还是不能
因为你不知道它是以什么方式遍历得到的这个序列
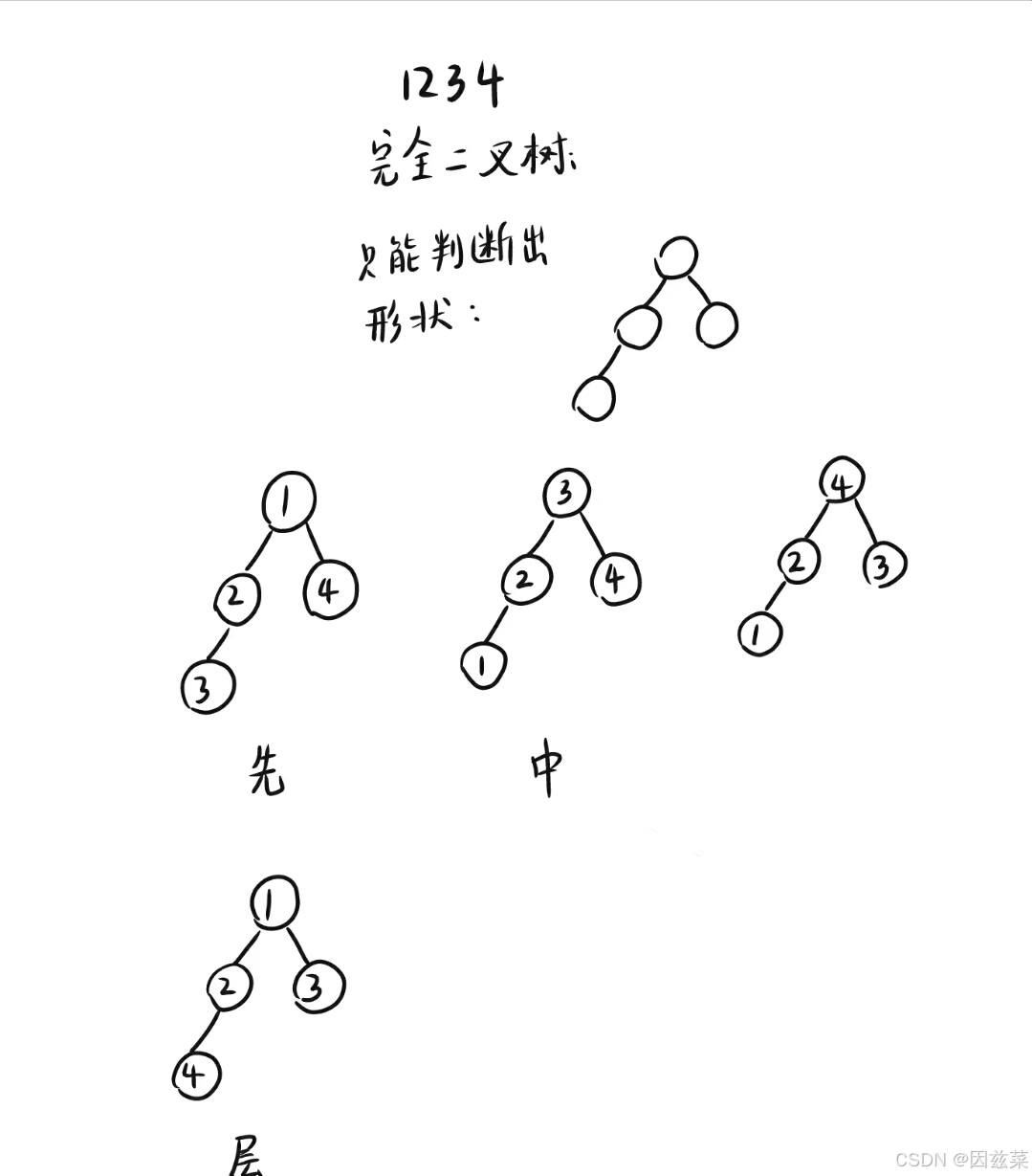
所以不仅需要序列,还需要知道是什么方式遍历得到的序列
由完全序列确定二叉树
2.当然,不是所有的树都是完全二叉树。在顺序存储中提到引入虚拟结点,这里有异曲同工之妙,只需要在序列中以特殊字符代替不存在的结点组成一个“完全序列”(即完全二叉树的遍历序列),那么拥有了这么一个含特殊字符的完全序列和遍历的顺序之后,我们可以还原出二叉树吗?
先给出结论:
后序遍历和前序遍历可以,中序遍历不行
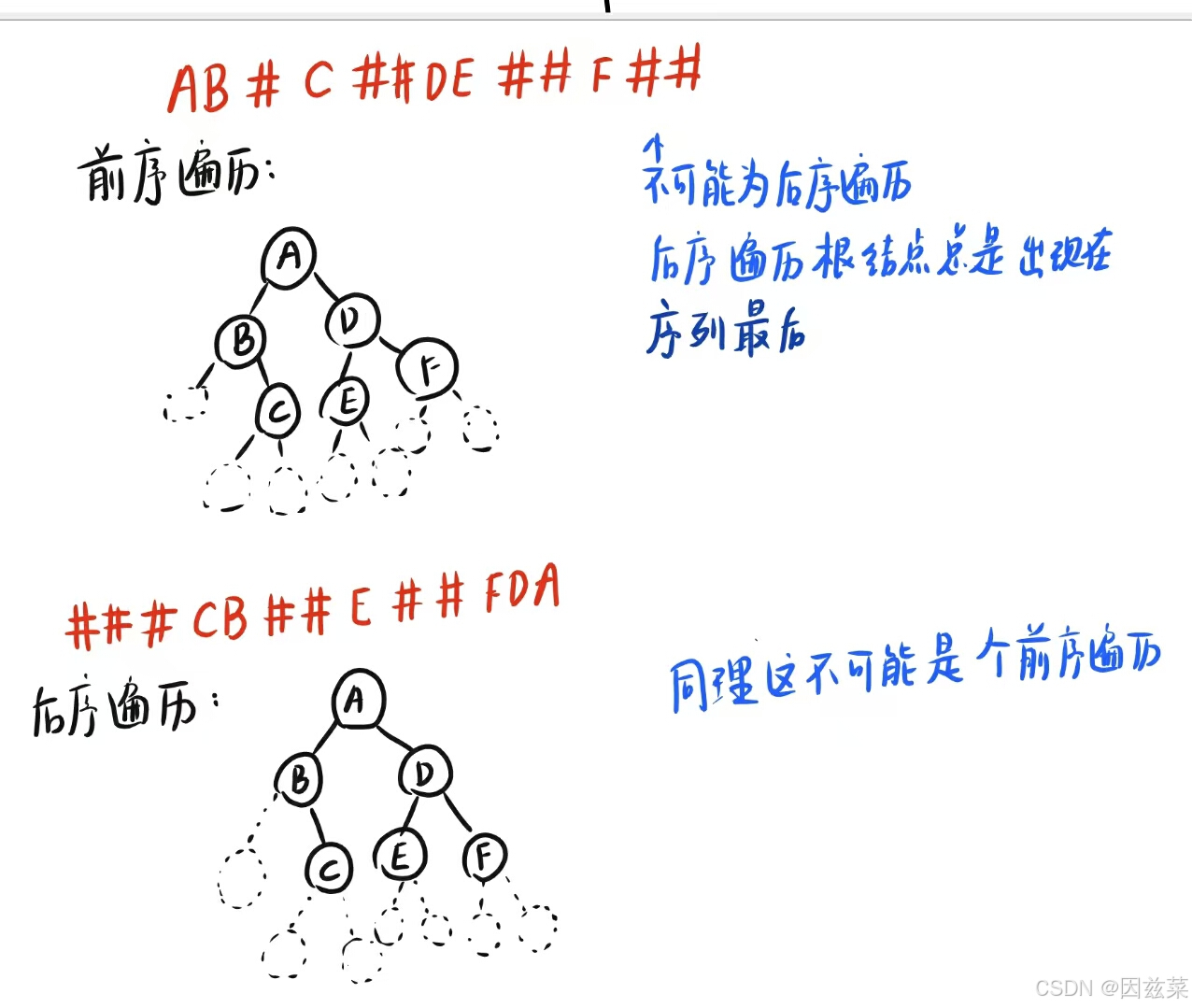
观察这个图,可以发现“#”起到一个“封底”的作用
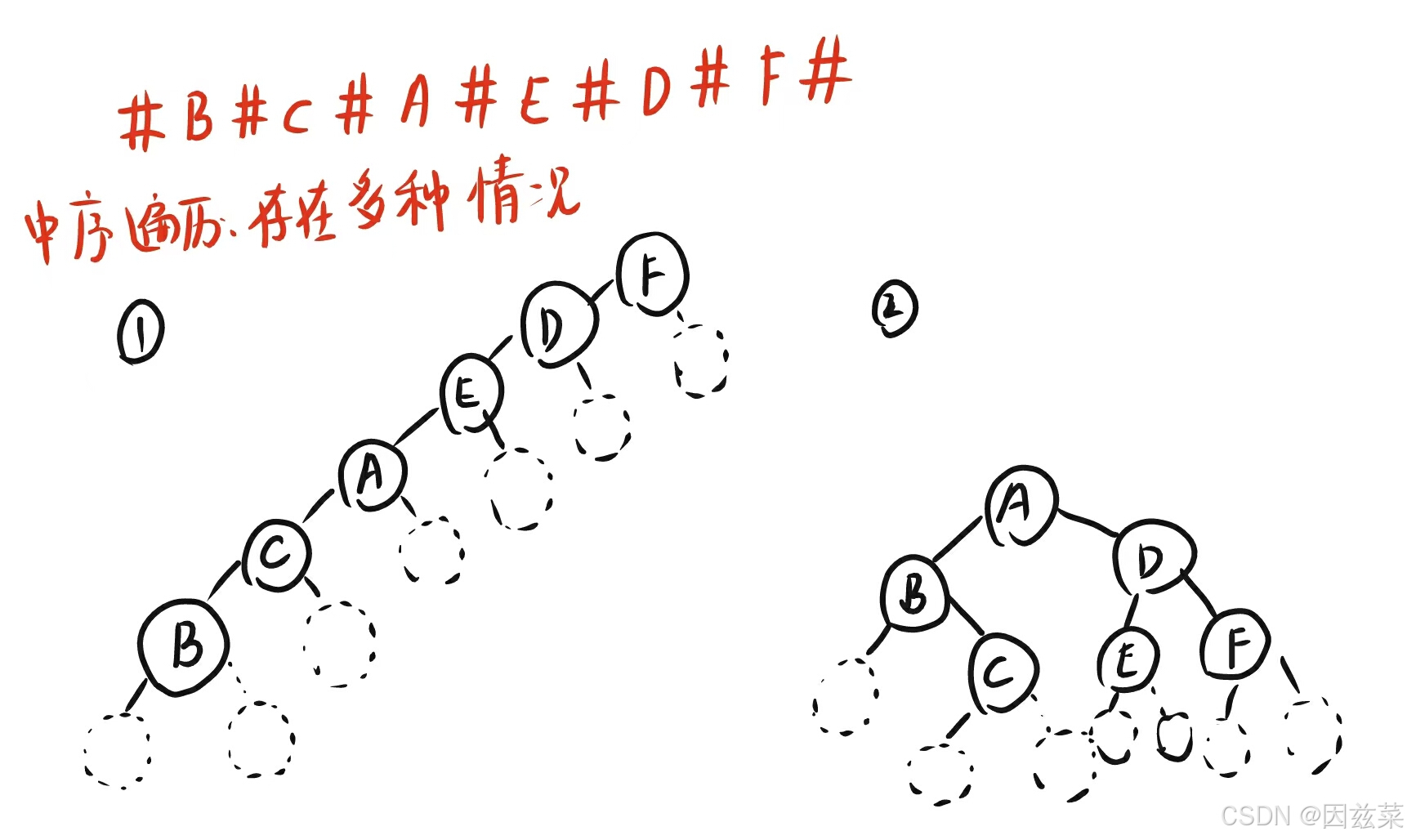
如图,一个中序遍历得到的完全序列是无法确定唯一的二叉树的
由前序遍历得到的完全序列建立二叉树
treeNode* createBiTreeFromPre(char* preorder, int* num) {
//preOrder储存了前序遍历得到的字符串,num用来追踪当前遍历的字符位置
char value = preorder[*num];
if (value == '#') {
(*num)++;
return NULL;
}
else {
treeNode* newNode = (treeNode*)malloc(sizeof(treeNode));
newNode->value = value;
(*num)++;
newNode->left = createBiTreeFromPre(preorder, num);
newNode->right = createBiTreeFromPre(preorder, num);
return newNode;
}
}
由层序遍历得到的完全序列建立二叉树
// 从层级遍历序列恢复二叉树
treeNode* buildTree(int* levelOrder, int n) {
if (n == 0) return NULL;
cqueue queue;
initQueue(&queue);
treeNode* root = createNewNode(levelOrder[0]); // 根节点
enQueue(&queue,levelOrder[0]); // 将根节点压入队列
int i = 1;
while (i < n) {
treeNode* currentNode;
outQueue(&queue, ¤tNode); // 从队列中取出当前节点
// 处理左子节点
if (i < n && levelOrder[i] != -1) { // -1 表示空节点
currentNode->left = createNewNode(levelOrder[i]);
enQueue(&queue, currentNode->left); // 左子节点入队
}
i++;
// 处理右子节点
if (i < n && levelOrder[i] != -1) {
currentNode->right = createNewNode(levelOrder[i]);
enQueue(&queue, currentNode->right); // 右子节点入队
}
i++;
}
return root;
}
由两种遍历序列确定唯一二叉树
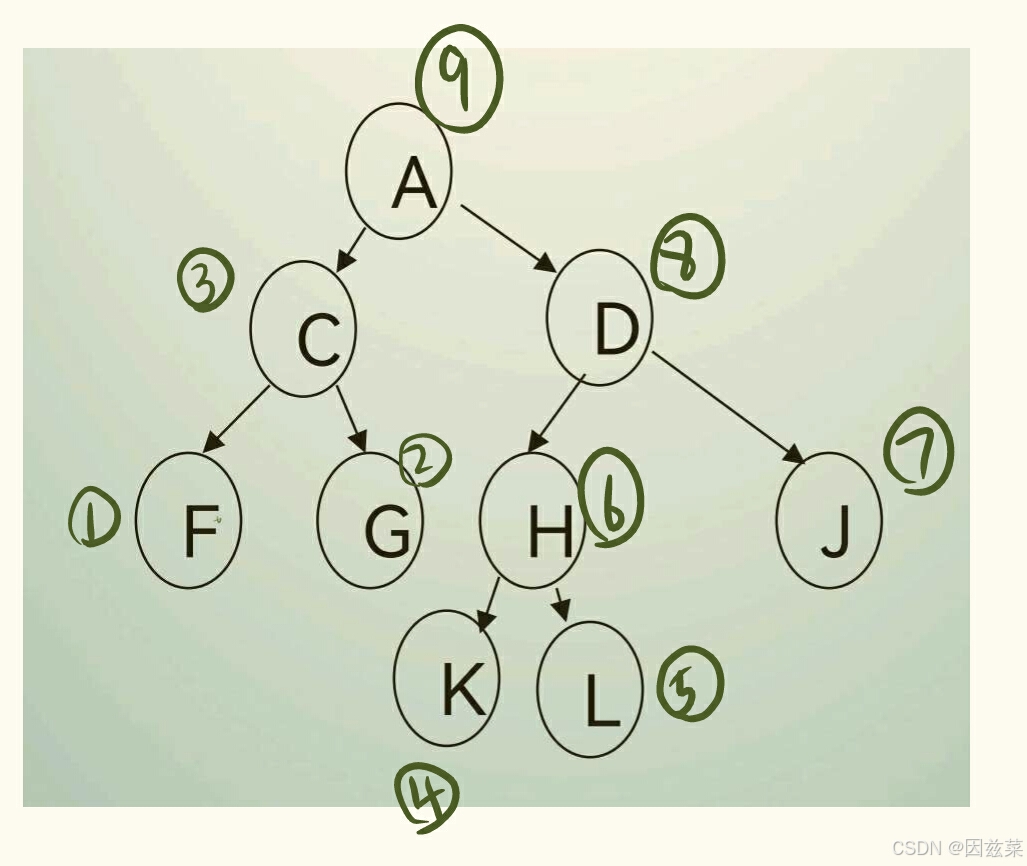
3.给出两种遍历方式得到的序列(这里是指普通序列,非完全序列)
可以还原出二叉树吗?
结论: 给出中序遍历得到的序列 + 前序/后序/层级遍历 之一得到的序列 可以还原出一棵二叉树
即三种情况: a.中序 + 后序 b.中序+前序 c.中序+层级遍历顺序
为什么中序遍历如此重要呢? 因为中序遍历得到的结果可以体现一个树根的左子根和右子根含有哪些元素。
那么如何具体还原呢?
1.看前序/后序/层级 确定树根元素
2.找到中序遍历中树根元素所在的位置,其左边的所有元素都在左根,右边的所有元素都在右根;
3.把左边的所有元素在前序(后序)中圈出来(其一定是全部挨在一起的),如果是前序遍历,第一个元素就是根的左孩子,右边所有元素的第一个元素就是根的右孩子;如果是后序遍历,则左边所有元素的最后一个元素是根的左孩子,右边所有元素的最后一个元素是根的右孩子。
4.再去中序遍历中找根的左孩子的位置,其左边的元素和右边的元素又分别是根的左孩子的左孩子和根的左孩子的右孩子的.以此类推..
直至所有元素的位置都被确定
说起来有些复杂,直接看图很简单

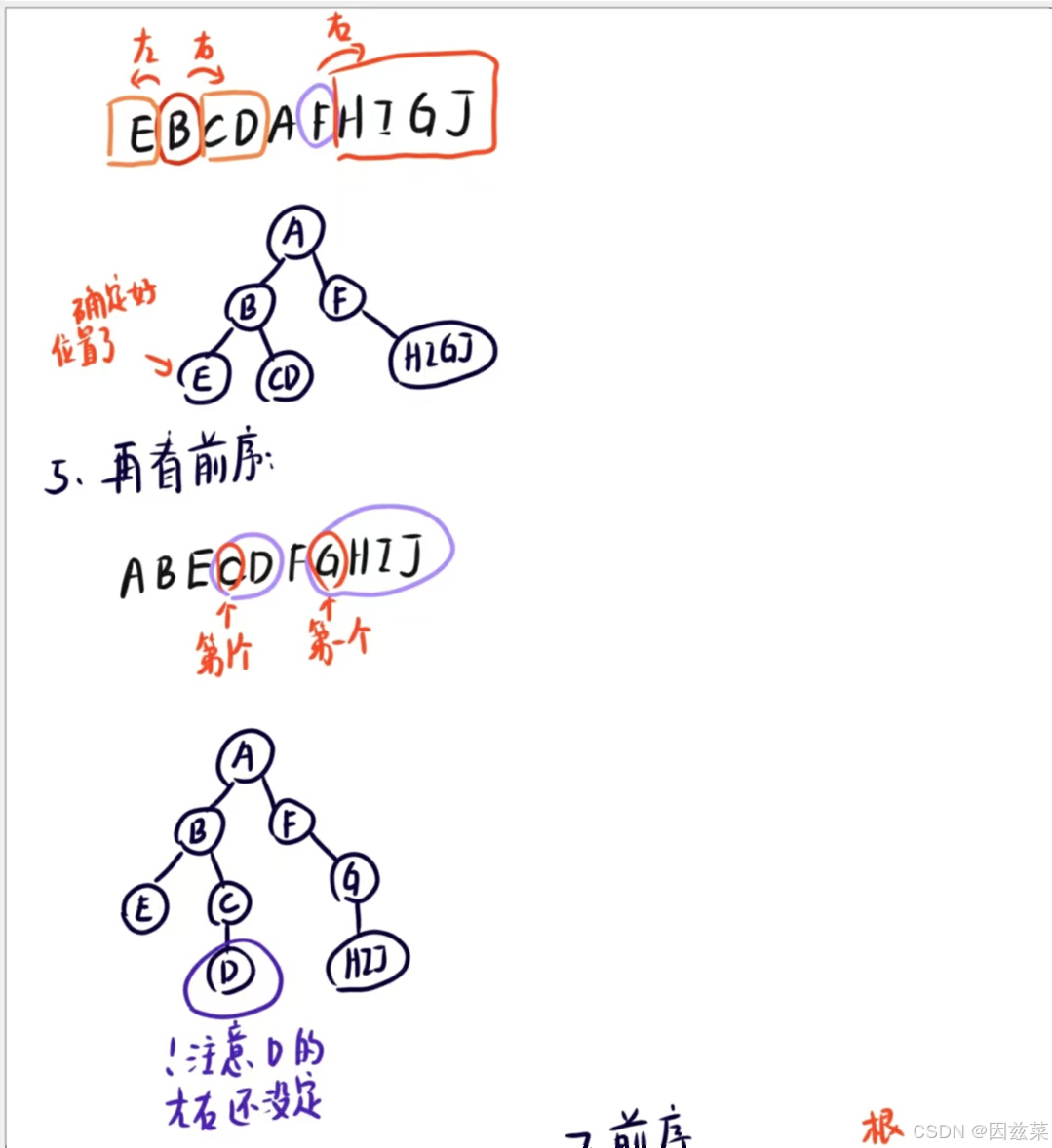
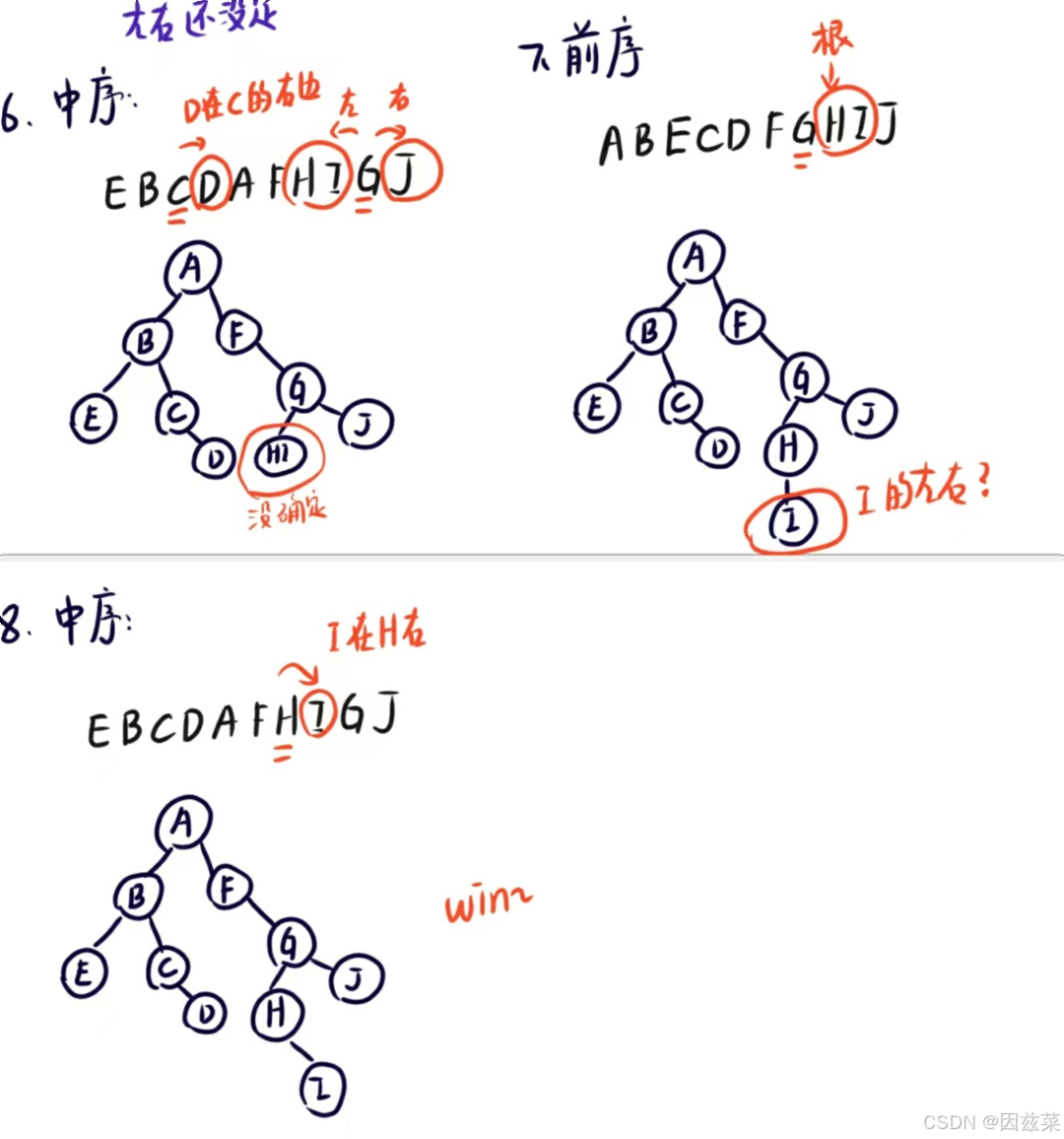
总之就是交替看两种顺序,一个定根,一个分左右
总结 何时能确定唯一的二叉树?
1.是完全二叉树,知道遍历方式;
2.不是完全二叉树,有完全序列,是后根/前根/层级遍历
3.知道中根遍历+任意一种遍历 的结果





















 2934
2934

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










