Lena and Matrix

情空黑夜

已于 2022-07-21 20:01:56 修改

阅读量155

点赞数

CC 4.0 BY-SA版权

分类专栏：观察文章标签：思维观察

于 2022-07-21 19:36:07 首次发布

本文链接：https://blog.youkuaiyun.com/qq_63010655/article/details/125919395

观察专栏收录该内容

5 篇文章

订阅专栏

该博客主要讨论了一种矩阵问题，其中矩阵由字符W和B组成。目标是找到一个点，使得该点到矩阵中所有B点的曼哈顿距离之最大值最小。博主提出了一个解决方案，首先找出矩阵中最接近的B点的四个角（左上、左下、右上、右下），然后遍历矩阵中的每个点，计算其到这四个角的最大曼哈顿距离，并取最小值。最终找到的点即为所求。代码中详细展示了这一过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

传送门

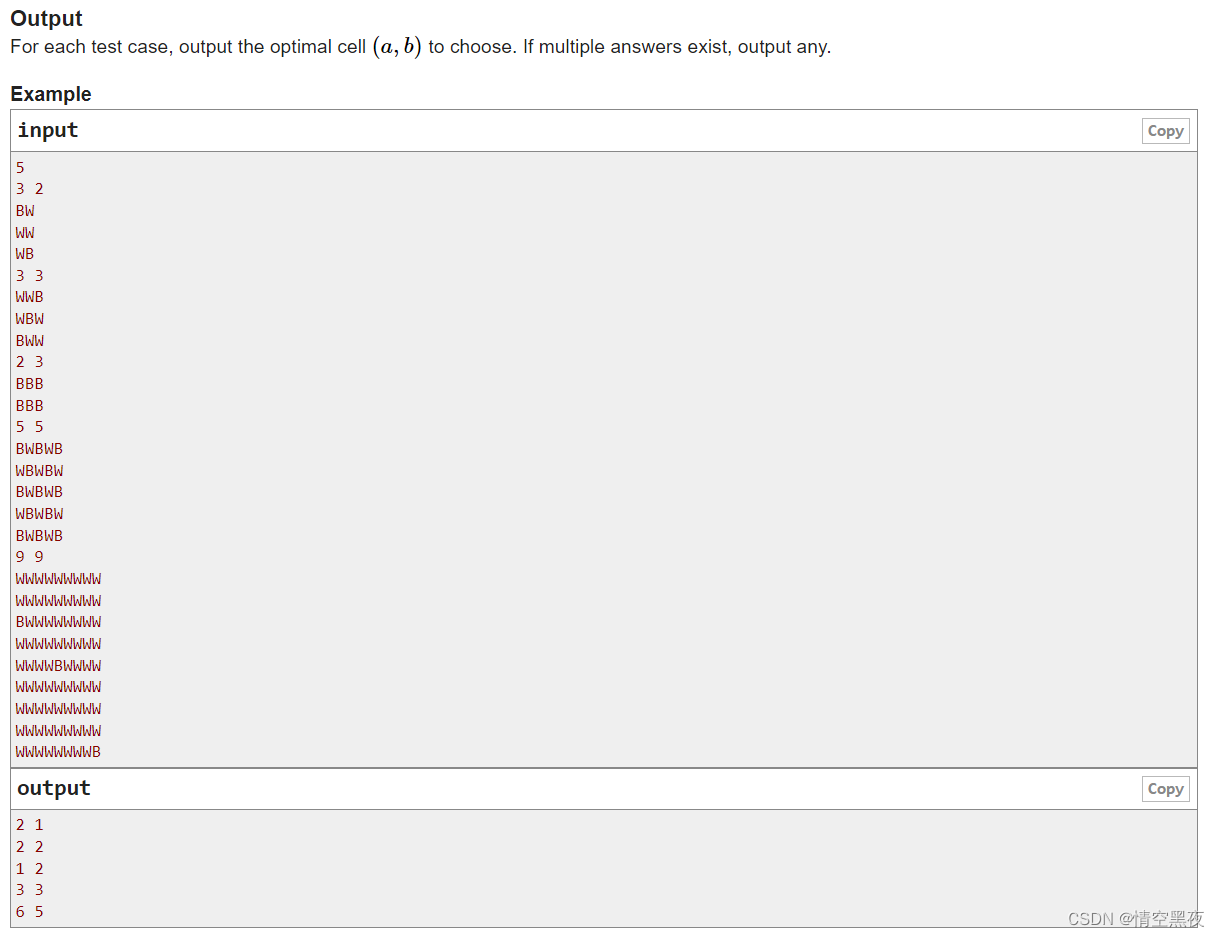
题意：

一个矩阵，由W和B组成，求其中一个点，这个点要满足到B的曼哈顿距离的最大值要最小，求出这个点

思路：

通过观察可以发现，一个点到B的最大曼哈顿距离必然是B的左上，左下，右上，右下点，可以任选点进行枚举证明，那就先求出这4个点，然后在枚举每一个点，到这4个点的最大距离的最小值，最后去min, 就是答案，这里找这4个点有一个技巧，找离一个点最近的点，可以通过枚举距离实现，距离从0开始枚举

#include <bits/stdc++.h>
#define endl '\n'
#define IOS ios::sync_with_stdio(false);
using namespace std;

typedef long long ll;
const int N = 1e3 + 10;
int T, n, m;
char w[N][N];
int ltx, lty, lbx, lby, rtx, rty, rbx, rby;

int check(int i, int j) {
    int ans = -1;
    ans = max(ans, abs(ltx - i) + abs(lty - j));
    ans = max(ans, abs(lbx - i) + abs(lby - j));
    ans = max(ans, abs(rtx - i) + abs(rty - j));
    ans = max(ans, abs(rbx - i) + abs(rby - j));
    return ans;
}

int main()
{
	IOS; cin.tie(0), cout.tie(0);
    cin >> T;
    while (T--)
    {
        cin >> n >> m;
        ltx = 1, lty = 1, lbx = 1, lby = 1, rtx = 1, rty = 1, rbx = 1, rby = 1;
        for (int i = 1; i <= n; ++i)
        {
            for (int j = 1; j <= m; ++j)
            {
                cin >> w[i][j];
            }
        }

        //找到最左上的点
        for (int dis = 0; dis <= n + m - 2; ++dis)  //dis的最远距离就是在(n, m)点，这个点离他最远距离才n + m - 2
        {
            for (int i = 1; i <= n; ++i)    //从最上面开始找  dis = i + j - 2
            {
                int j = dis - i + 2;
                if (1 <= j && j <= m && w[i][j] == 'B') //说明找到了
                {
                    ltx = i;
                    lty = j;
                    goto a;
                }
            }
        }
        a: ;
        //找左下的点
        for (int dis = 0; dis <= n + m - 2; ++dis)
        {
            for (int i = n; i >= 1; --i)       // dis = n - i + j - 1
            {
                int j = dis + i - n + 1;
                if (1 <= j && j <= m && w[i][j] == 'B')
                {
                    lbx = i;
                    lby = j;
                    goto b;
                }
            }
        }
        b: ;
        //找右上的点
        for (int dis = 0; dis <= n + m - 2; ++dis)
        {
            for (int i = 1; i <= n; ++i)
            {
                int j = i - 1 + m - dis;
                if (1 <= j && j <= m && w[i][j] == 'B')
                {
                    rtx = i; 
                    rty = j;
                    goto c;
                }
            }
        }
        c: ;
        //找右下的点
        for (int dis = 0; dis <= n + m - 2; ++dis)
        {
            for (int i = n; i >= 1; --i)
            {
                int j = n - i + m - dis;
                if (1 <= j && j <= m && w[i][j] == 'B')
                {
                    rbx = i;
                    rby = j;
                    goto d;
                }
            }
        }
        d: ;
        int ansx = 1, ansy = 1, minn = 1e9;
        for (int i = 1; i <= n; ++i)
        {
            for (int j = 1; j <= m; ++j)
            {
                int temp = check(i, j);
                if (minn > temp)
                {
                    minn = temp;
                    ansx = i;
                    ansy = j;
                }
            }
        }
        //cout << ltx << " " << lty << " " << lbx << " " << lby << " " << rtx << " " << rty << " " << rbx << " " << rby;
        cout << ansx << " " << ansy << endl; 
    }
	return 0;
}