控制系统在Matlab上的实现(2)

最新推荐文章于 2024-09-27 14:54:20 发布

THE greatest KingBob

最新推荐文章于 2024-09-27 14:54:20 发布

阅读量691

点赞数 10

CC 4.0 BY-SA版权

文章标签：算法

本文链接：https://blog.youkuaiyun.com/qq_62743549/article/details/142166455

1.模型建立与化简

框图化简是将复杂系统转化为典型环节传递函数，实现系统建模的一种等效交换方法

1.1 串联结构

G1 = tf([2,5,1],[1,2,3]);
G2 = zpk(-2,-10,5);
G = G1*G2

结果：

G =
 
  10 (s+2.281) (s+2) (s+0.2192)
  -----------------------------
      (s+10) (s^2 + 2s + 3)
 
连续时间零点/极点/增益模型。

1.2 并联结构

% 并联结构
G1 = tf([2,5,1],[1,2,3]);
G2 = zpk(-2,-10,5);
G = G1+G2

结果：

G =
 
  7 (s+0.6837) (s^2 + 5.745s + 8.358)
  -----------------------------------
         (s+10) (s^2 + 2s + 3)
 
连续时间零点/极点/增益模型。

1.3 反馈结构

%反馈结构
G1 = tf([2,5,1],[1,2,3]);
G2 = zpk(-2,-10,5);
G = feedback(G1,G2,-1)  % 1表示正反馈，-1表示负反馈，默认为负反馈

结果：

G =
 
  0.18182 (s+0.2192) (s+2.281) (s+10)
  -----------------------------------
   (s+3.419) (s^2 + 1.763s + 1.064)
 
连续时间零点/极点/增益模型。

1.4 复杂结构

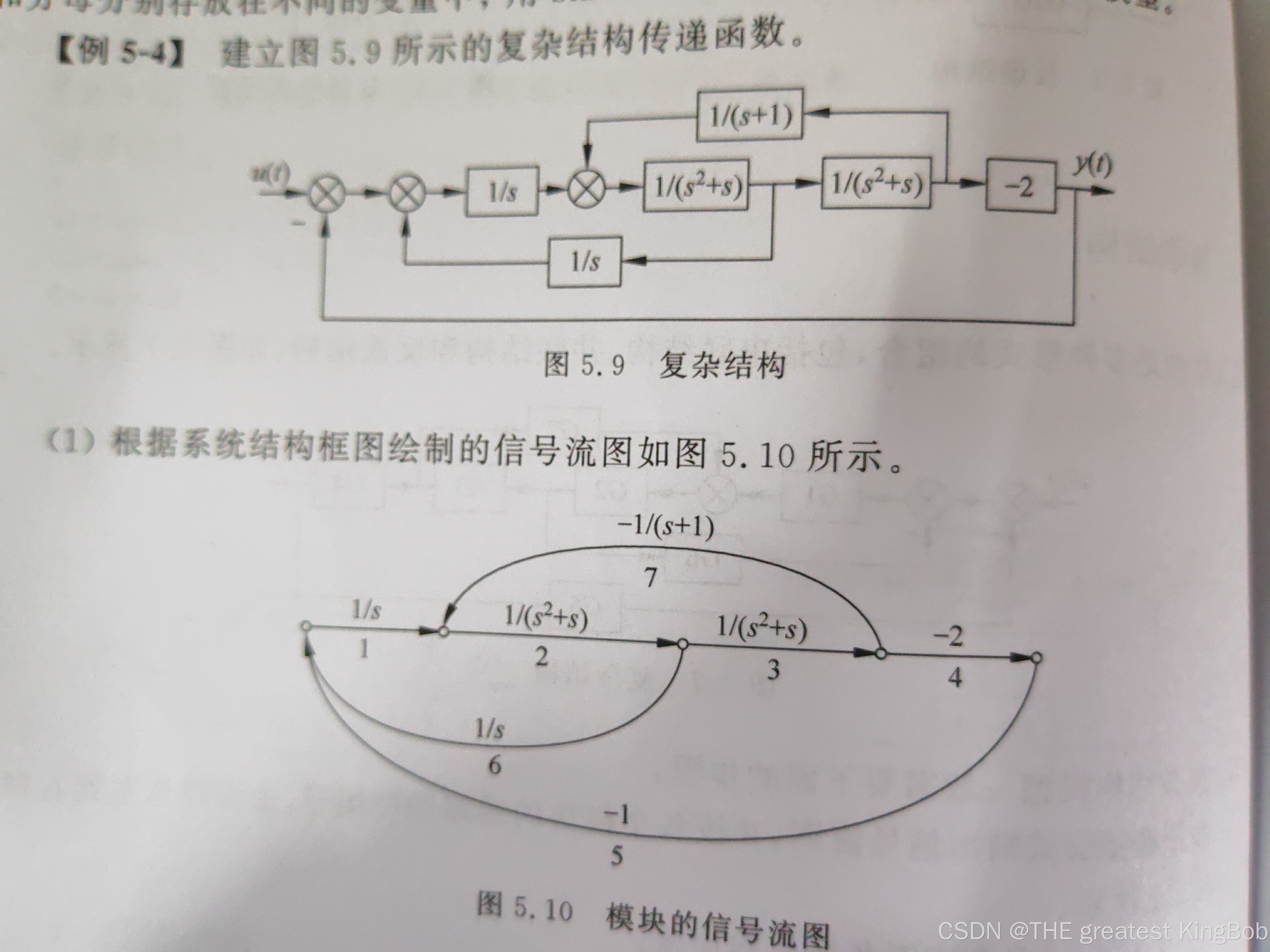
%复杂结构

% 1.使用append命令实现各模块的链接
G1 = tf(1,[1,0]); G2 = tf(1,[1,1,0]); G3 = tf(1,[1,1,0]); G4 = tf(-2,1); G5 = tf(-1,1); G6 = tf(1,[1,0]); G7 = tf(-1,[1,1]);
Sys = append(G1,G2,G3,G4,G5,G6,G7);

% 2.指定各模块链接关系
Q = [1,6,5;   %第一列为模块通路编号，后面则为进入该节点的模块的通路编号
     2,1,7;
     3,2,0;
     4,3,0;
     5,4,0;
     6,2,0;
     7,3,0];

% 3.指定系统总体输入/输出
INPUTS = 1;
OUTPUTS = 4;   


% 4.使用connect命令建立整个系统的模型
G = connect(Sys,Q,INPUTS,OUTPUTS)

结果：

G =
 
  A = 
       x1  x2  x3  x4  x5  x6  x7
   x1   0   0   0   0   2   1   0
   x2   1  -1   0   0   0   0  -1
   x3   0   1   0   0   0   0   0
   x4   0   0   1  -1   0   0   0
   x5   0   0   0   1   0   0   0
   x6   0   0   1   0   0   0   0
   x7   0   0   0   0   1   0  -1
 
  B = 
       u1
   x1   1
   x2   0
   x3   0
   x4   0
   x5   0
   x6   0
   x7   0
 
  C = 
       x1  x2  x3  x4  x5  x6  x7
   y1   0   0   0   0  -2   0   0
 
  D = 
       u1
   y1   0
 
连续时间状态空间模型。

不知道为什么是一堆矩阵？？？