二叉搜索树实现-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_62712350/article/details/129829358

本文介绍了二叉搜索树的基本概念，包括其特性，以及如何在树中搜索、插入新节点和删除节点的详细过程。搜索操作的时间复杂度在最好情况下为logN，最坏情况下为N。插入操作利用搜索找到合适位置，并插入新节点。删除操作则需要考虑节点是否有左右孩子，以及如何调整结构以保持树的平衡。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

什么是二叉搜索树?

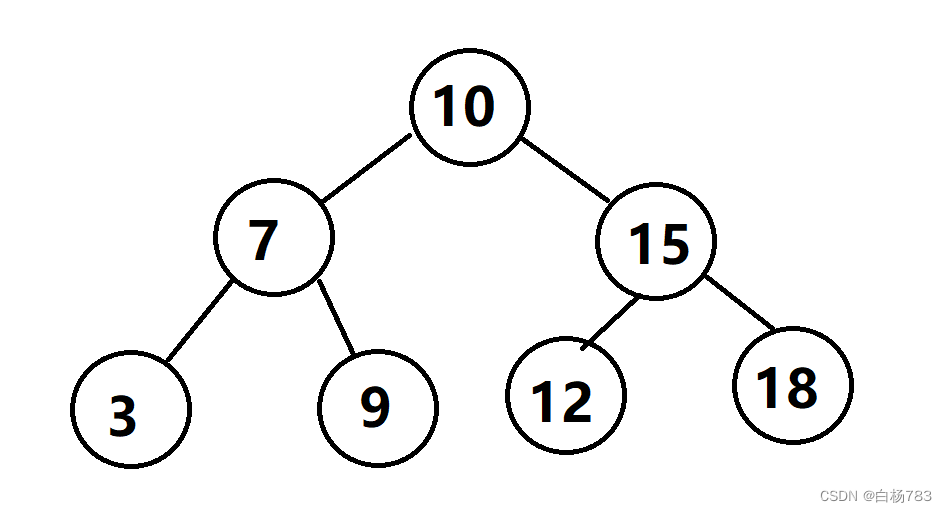
如图,就是一颗二叉搜索树,该树中,任意节点的左子树的任意值,比该节点小,右子树的任意值比该节点大.

二叉搜索树的实现

二叉树的搜索

给定一个数,我们到底如何在二叉树中寻找?

代码实现

 public TreeNode search(int key){
        TreeNode cur = root;
        while(cur != null){
            if(cur.val > key){
                cur = cur.left;
            } else if(cur.val < key){
                cur = cur.right;
            }else{
                return cur;
            }
        }
        return null;
    }

由上述二叉搜索树的特性,不难知道如果要在二叉搜索树中查找一个数,时间复杂度最好的情况下为logN(满二叉树),最差的情况下为N(二叉搜索树为单分支的情况)

二叉搜索树的插入

首先我们要知道的是,在二叉搜索树中,是不能有俩个值相同的节点的.
实现二叉树的插入,我们可以利用搜索的思路,找到应该插入的位置,再进行插入.
要注意的是,我们要记录一下要插入位置的父亲节点,否则我们没有办法进行插入

代码

public boolean insert(int key){
        TreeNode parent = null;
        TreeNode cur = root;
        while(cur!=null){
            if(cur.val > key){
                parent = cur;
                cur = cur.left;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else{
                return false;
            }
        }
        TreeNode node = new TreeNode(key);
        if(parent.val > key){
            parent.left = node;
        }else{
            parent.right = node;
        }
        return true;
    }

二叉搜索树的删除

二叉搜索树的删除比较麻烦一点,因为当我们删除掉一个节点的时候往往要,调整它的子节点.

我们可以采取分情况讨论的方式,可以分为三种情况
1.要删除的节点没有左孩子
2.要删除的节点没有右孩子
3.要删除的节点左右孩子都有

一:要删除的节点没有左孩子中,也分三种情况,1.如果这个节点是根节点的话,我们直接把它的右孩子当作新的根.2.如果要删除的节点是它的父亲节点的左孩子,此时可以把要删除节点的右孩子当作要删除节点的父亲节点新的左孩子.3.如果要删除的节点是它的父亲节点的右孩子,此时可以把要删除节点右孩子当作要删除节点父亲节点新的右孩子.

二:要删除的节点没有右孩子,同理

三:要删除的节点左右孩子都有的情况下,我们可以在要删除节点的左子树中找到一个最大的数,或者在要删除的节点右子树中找到一个最小的数去删除,再把要删除节点的值改为被删除节点的值,这样这个被找到的最大值(或最小值)就代替了我们要删除的节点

代码实现

public void remove(int key){
        TreeNode parent = null;
        TreeNode cur = root;
        while(cur != null){
            if (cur.val > key) {
                parent = cur;
                cur = cur.left;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else {
                removeNode(parent,cur);
            }
        }
    }

    private void removeNode(TreeNode parent, TreeNode cur) {
        if(cur.left == null){
            if(cur == root){
                cur = cur.right;
            }else if(parent.left == cur){
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null){
            if(cur == root){
                cur = cur.left;
            }else if(parent.left == cur){
                parent.left = cur.left;
            }else{
                parent.right = cur.left;
            }
        }else{
            TreeNode target = cur.left;
            TreeNode targetparent = cur;
            while(target.right != null){
                targetparent = target;
                target = target.right;
            }
            cur.val = target.val;
            if(targetparent.left == target){
                targetparent.left = target.left;
            }else{
                targetparent.right = target.left;
            }
        }
    }