辗转相除法
什么是辗转相除法?
辗转相除法:辗转相除法是求两个自然数的最大公约数的一种方法,也叫欧几里德算法。
辗转相除法是如何求俩个自然数的最大公约数的?
话不多说上例题:
例如,求(319,377):
∵ 319÷377=0(余319)
∴(319,377)=(377,319);
∵ 377÷319=1(余58)
∴(377,319)=(319,58);
∵ 319÷58=5(余29)
∴ (319,58)=(58,29);
∵ 58÷29=2(余0)
∴ (58,29)= 29;
∴ (319,377)=29。
简单来说,现在有a,b俩个数,先拿a除以b得到余数c,如果c不等于0的话,就把除数b的值赋给a,把余数c的值赋给b,再拿新的a除以新的b,得到新的c以此类推……如果得到的余数c等于0的话,那么之前的除数b就是最大公约数。
求俩个数的最大公约数
public static void main(String[] args) {
int a = 319;
int b = 377;
int c = a % b;
while(c != 0){
a = b;
b = c;
c = a % b;
}
System.out.println("最大公约数 "+b);
}
求俩个数的最小公倍数
最小公倍数=两数的乘积/最大公约(因)数
代码和上题类似
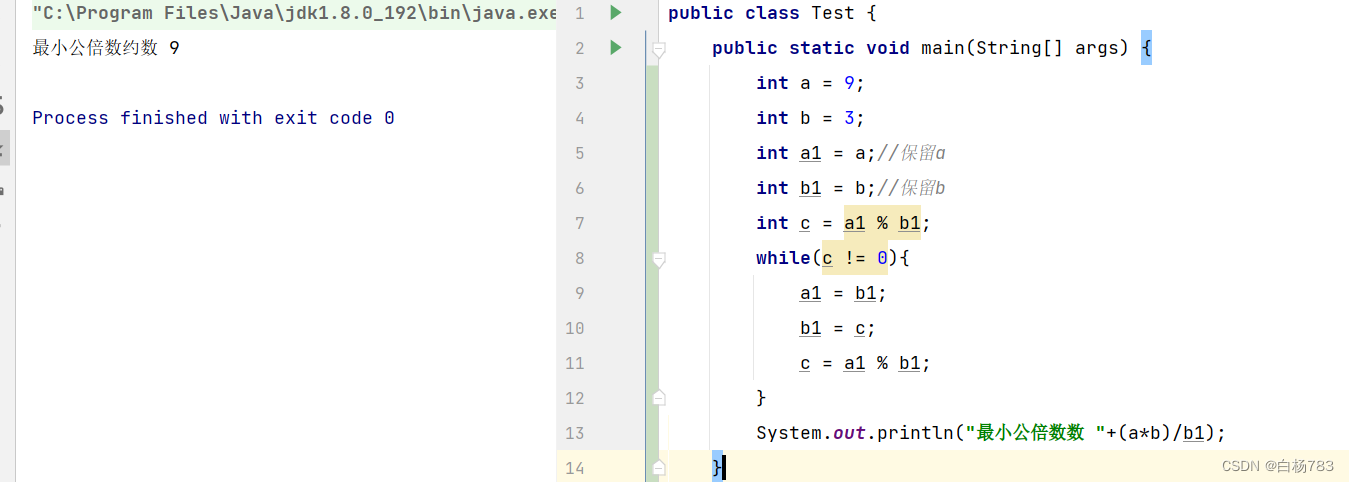
public static void main(String[] args) {
int a = 9;
int b = 3;
int a1 = a;//保留a
int b1 = b;//保留b
int c = a1 % b1;
while(c != 0){
a1 = b1;
b1 = c;
c = a1 % b1;
}
System.out.println("最小公倍数数 "+(a*b)/b1);
}























 2054
2054

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








