洛谷 P1226 【模板】快速幂||取余运算

题目描述

给你三个整数 a,b,p，求 a^b mod p。

输入格式

输入只有一行三个整数，分别代表 a,b,p。

输出格式

输出一行一个字符串 a^b mod p=s，其中 a,b,p 分别为题目给定的值， s为运算结果。

思路

很久之前当我还只会循环时就尝试过这道题，结果当然是美美WA了。今天本来应该学高精除法不知道为啥又开始学快速幂。看了dalao的解析才好不容易学会。

简化的第一步：
由数学知识可得：
(a * b) % p = (a % p * b % p) % p

也就是说，一个合数的模等于它两因数分别取模相乘后再取模。一般化的结论即为，多个因子乘积的模==每个因子分别取模再相乘再取模。因子取模后当然会减小，减小乘数，进行乘法的速度就会提高。

原来只用循环的代码长这样：

while(b--){
	res*=a;
}
res%=p;

用这个公式优化后长这样：

while(b--){
		int m=a%p;
		res%=p;
		res*=m;
	}
	res%=p;

简化的第二步：

快速幂算法能帮我们算出指数非常大的幂，传统的求幂算法之所以时间复杂度非常高（为O(指数n)），就是因为当指数n非常大的时候，需要执行的循环操作次数也非常大。所以我们快速幂算法的核心思想就是每一步都把指数分成两半，而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小，所需要执行的循环次数也变小，而最后表示的结果却一直不会变。
原文链接：https://blog.youkuaiyun.com/qq_19782019/article/details/85621386

求快速幂过程可以简化为这样的递归算法：
若b%2==0&&b!=2  -->return a^(b/2)*a^(b/2)

若b%2==1 -->return a*a^(b-1)

若b==0 --> return 1

代码如下：

while(b){
    	if(b%2==0){
    		b/=2;
    		a*=a;
    		a%=p;
		}else{
			b/=2;
			res*=a;
			res%=p;
			a*=a;
			a%=p;
		}
	}

简化的第三步：

由于计算机内部实际上是把+ - * / 转化为位运算来进行计算的，所以如果我们在代码中直接使用位运算的话速度会更快。

位运算的一些基本知识：

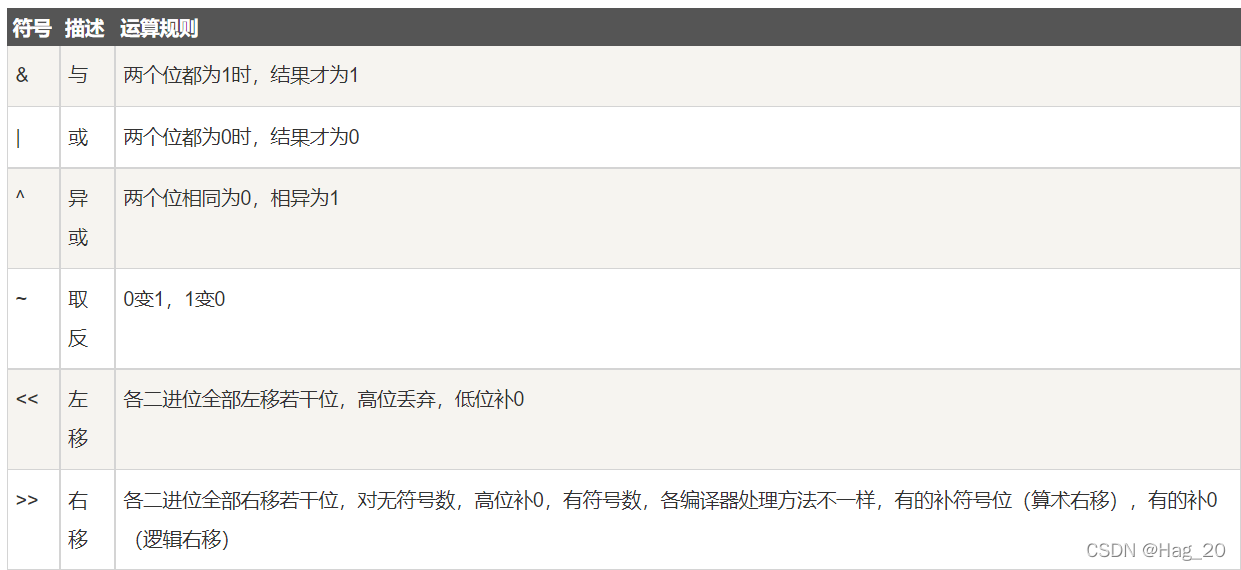
 显然，用位运算我们可以完成判断奇偶性的操作：若判断数字为奇数，则其二进制末位为1。与1进行与运算后结果为1。同样，偶数和1进行与运算后结果为0.

b/=2的操作也可以使用位运算。原理和分解十位整数的原理相近：设a为十进制数，“砍掉”末位相当于给a整除10 。

那么对于二进制数，如果想对它进行除二操作，“砍掉”它的最后一位，即将每一个数字全部右移一位。

代码如下：

while(b){
    	if(b&1==0){//相当于当b为偶数时 
    		b>>=1;
    		a*=a;
    		a%=p;
		}else{
			b>>=1;
			res*=a;
			res%=p;
			a*=a;
			a%=p;
		}
	}

完整代码：

#include<stdio.h>
typedef long long ll;
int main(){
	ll a,b,p;
	ll b1;
	scanf("%lld %lld %lld",&a,&b,&p);
	b1=b;
	ll res=1;
	ll a1=a;
	while(b){
    	if(b&1==0){//相当于当b为偶数时 
    		b>>=1;
    		a*=a;
    		a%=p;
		}else{
			b>>=1;
			res*=a;
			res%=p;
			a*=a;
			a%=p;
		}
	}
	printf("%lld^%lld mod %lld=%lld",a1,b1,p,res%p);
	return 0;
}