HNU_多传感器（专选）_作业3（贝叶斯，Dempster合成规则）

参考：

第2题：D-S证据合成理论+TBM推理实例 - 知乎

第3题：多源测试信息融合真题 - 豆丁网

一. 简答题（共3题，100分）

1. (简答题)贝叶斯定理

题目1：某工厂有4条流水线生产同一种产品，

4条流水线的产量分别占总产量的 15%，20%, 30%, 35% ，

且这4条流水线的不合格品率依次为 0.05，0.04，0.03及 0.02。

（1）现在从该厂产品中任取一件，问恰好抽到不合格品的概率为多少？

（2）若该厂规定，出了不合格品要追究有关流水线的经济责任。在出厂产品中任取一件，结果为不合格品，但该件产品是哪一条流水线生产的标志已脱落，问厂方如何处理这件不合格品比较合理？第 4条流水线应该承担多大责任？

我的答案：

（1）设Ai为从第i条流水线抽到产品，B为不合格产品：【全概率公式】

P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)+P(A4)P(B|A4)

       =0.15*0.05+0.2*0.04+0.3*0.03+0.35*0.02=0.0075+0.008+0.009+0.007=0.0315

（2）

贝叶斯定理：

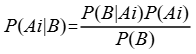
第4条流水线的责任：

        

        第4条流水线承担22.22%的责任

2. (简答题)Dempster合成规则-嫌疑人

题目2：根据Dempster合成规则补全下表

某宗“谋杀案” 的三个犯罪嫌疑人组成了识别框架Q ={Peter, Paul, Mary} ，

目击证人（W1, W2）分别给出下表所示的基本概率数（BPA）。

我的答案：

（1）归一化常数K：

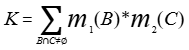
K = m1(Peter)*m2(Peter)+m1(Paul)*m2(Paul)+m1(Mary)*m2(Mary)

  = 0.98*0+0.01*0.01+0.01*0.99=0.01

（2）组合mass函数：

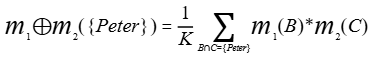
Peter： m1(Peter)*m2(Peter)  / K = 0.98*0/0.01=0

Paul：  m1(Paul)*m2(Paul)     / K = 0.01*0.01/0.01=0.01

Mary:    m1(Mary)*m2(Mary)   / K = 0.01*0.99/0.01=0.99

3. (简答题)Dempster合成规则-医生诊病

题目3：假设两个医生给同一个病人诊断疾病，

甲医生认为感冒的可能性是0.9，说不清病症的可能性是0.1；

乙医生认为0.2的可能性是肺炎，0.8的可能性是说不清楚的病症；

请问患者是感冒的可能性落在什么范围？写出mass函数，并用dempster合成规则求解。

 我的答案：

（1）定义问题中的质心：Q={感冒，说不清，肺炎}

甲医生：m1({感冒})=0.9；m1({说不清})=0.1；

乙医生：m2({肺炎})=0.2；m2({说不清})=0.8；

（2）应用Dempster合成规则

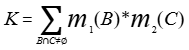
归一化常数K： 

K = m1({感冒})*m2({说不清})+m1({说不清})*m2({说不清})+m1({说不清})*m2({肺炎})

   = 0.9*0.8+0.1*0.8+0.1*0.2 = 0.82

（3）组合mass函数：

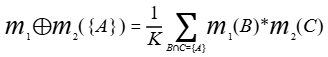
m({感冒})   = m1({感冒})*m2({说不清})      / K = 0.9*0.8/0.82 =0.878 

m({说不清})= m1({说不清})*m2({说不清})  / K = 0.1*0.8/0.82 =0.098

m({肺炎})    = m1({说不清})*m2({肺炎})      / K = 0.1*0.2/0.82 =0.024

（4）感冒的可能性：

①信任函数Bel：

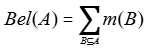
        Bel（感冒）= m（感冒）=0.878

②似然函数Pl：

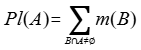
​        Pl（感冒） = m（感冒）+ m（说不清）=0.976

所以感冒的可能性为[0.878,0.976]，近似为[0.9,1]