1.实验目的:加深对二元关系性质的理解以及对自反闭包,对称闭包和传递闭包的运算
2.实验要求:
(1)能够判定给定的关系是否满足(反)自反性、(反)对称性、传递性。
(2)计算给定关系的自反闭包、对称闭包和传递闭包。
#include <iostream>
#include <cstdlib>
using namespace std;
int N;//集合A中元素的个数
char* A;//集合A中的元素
int** MR;//关系矩阵
//自反性
int Reflexivity() {
for(int i=0; i<N; i++) {
if(MR[i][i]==0) {
return 0;
}
}
return 1;
}
//对称性
int Symmetry() {
for(int i=0; i<N; i++) {
for(int j=0; j<=i; j++) {
if(MR[i][j]!=MR[j][i]) {
return 0;
}
}
}
return 1;
}
//传递性
int Transmission() {
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) {
if(MR[i][j]==1) {
for(int k=0; k<N; k++) {
if(MR[j][k]==1 && MR[i][k]!=1) {
return 0;
}
}
}
}
}
return 1;
}
//反自反性
int Irreflexivity() {
for(int i=0; i<N; i++) {
if(MR[i][i]==1) {
return 0;
}
}
return 1;
}
//反对称性
int Irsymmetry() {
for(int i=0; i<N; i++) {
for(int j=0; j<i; j++) {
if(MR[i][j]==MR[j][i] && MR[j][i]==1) {
return 0;
}
}
}
return 1;
}
//自反闭包
void ReflexiveClosure() {
cout <<"自反闭包:";
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) {
if(MR[i][j]==1 || (i==j && MR[i][j]==0)) {
cout << "<" <<A[i] <<","<<A[j] <<">" <<" ";
}
}
}
cout << endl;
}
//对称闭包
void SymmetricalClosure() {
cout <<"对称闭包:";
for(int i=0; i<N; i++) {
for(int j=0; j<=i; j++) {
if(MR[i][j]==1 || MR[j][i]==1) {
cout << "<" <<A[i] <<","<<A[j] <<">" <<" ";
if(i!=j) cout << "<" <<A[j] <<","<<A[i] <<">" <<" ";
}
}
}
cout << endl;
}
//传递闭包
void WarShall() {
int ** temp = MR;
cout <<"传递闭包:";
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) {
if(temp[j][i]) {
for(int k=0; k<N; k++) {
temp[j][k] += temp[i][k];
}
}
}
}
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) {
if(temp[i][j]) {
cout << "<" <<A[i] <<","<<A[j] <<">" <<" ";
}
}
}
cout << endl;
}
int FindIndex(char c) {
for(int i =0; i<N; i++) {
if(A[i]==c) {
return i;
}
}
cout << "程序退出!";
exit(0);
}
//初始化集合A和关系矩阵
void InitAAndMR() {
A = new char [N];
MR = new int* [N];
for(int i=0; i<N; i++) {
MR[i] = new int[N];
for(int j=0; j<N; j++) {
MR[i][j]=0;
}
}
}
void Input() {
cout << "请输入集合A中元素的个数:";
cin>>N;
InitAAndMR();
cout << "请输入集合A中的元素:";
for(int i = 0; i<N; i++) {
cin >> A[i];
}
int m;
cout << "请输入关系的个数:";
cin >>m;
cout << "请输入二元关系:";
char a,b;
for(int i=0; i<2*m; i++) {
if(i%2==0) {
cin >> a;
} else {
cin >> b;
}
if((i+1)%2==0 && i) {
MR[FindIndex(a)][FindIndex(b)]=1;
}
}
}
void Output() {
cout <<endl << "关系矩阵MR:" <<endl;
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) {
cout << MR[i][j] << " ";
}
cout << endl;
}
cout <<endl
<< "R满足"
<< (Reflexivity()?"自反性、":"")
<< (Symmetry()?"对称性、":"")
<<(Transmission()?"传递性、":"")
<< (Irreflexivity()?"反自反性、":"")
<< (Irsymmetry()?"反对称性":"")
<< endl << endl;
ReflexiveClosure();
SymmetricalClosure();
WarShall();
}
int main() {
Input();
Output();
return 0;
}
测试数据:
A={a,b,c,d}
R={<a,b>,<b,a>,<b,c>,<c,d>}
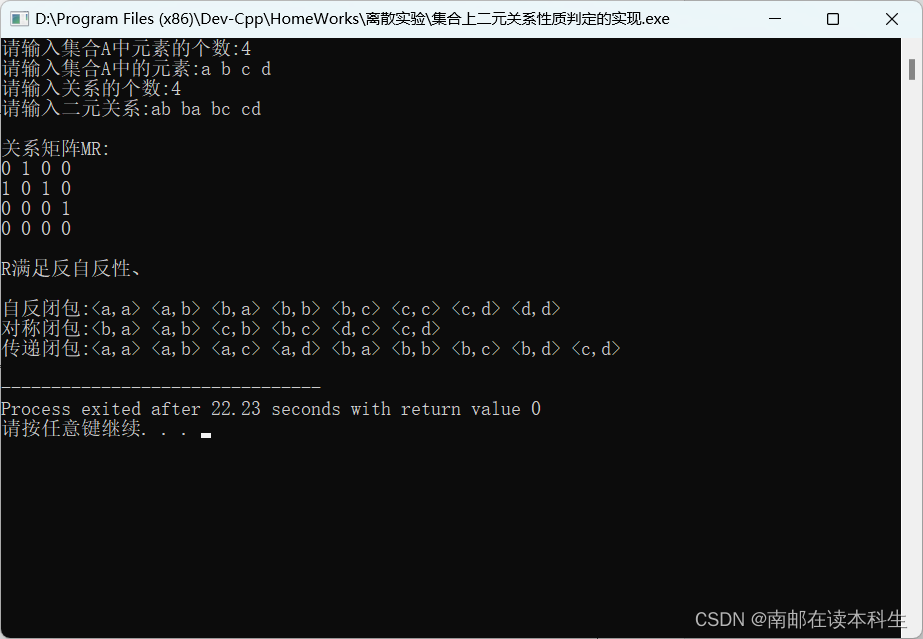
R满足反自反性
自反闭包:<a,a> <a,b> <b,a> <b,b> <b,c> <c,c> <c,d> <d,d>
对称闭包:<b,a> <a,b> <c,b> <b,c> <d,c> <c,d>
传递闭包:<a,a> <a,b> <a,c> <a,d> <b,a> <b,b> <b,c> <b,d> <c,d>

























 944
944

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










