目录
二.数据的表示和运算
2.1_1_进位计数制

罗马数字

十进制计数法

r进制计数法

任意进制->十进制

二进制<->八进制、十六进制

各种进制的常见书写方式

十进制->任意进制



真值和机器数

知识回顾和重要考点
二进制 <—> 八进制、十六进制补位
整数 高位补0
小数 低位补0

2.1_2_其余常见编码
BCD码
8421码,结果不在映射表里,加上6(0110)进行修正

余3码、2421码
有权码:8421码,2421码
无权码:余3码
2421码规定0~4第一位为0,5~9第一位为1

格雷码

过渡噪声
二进制码会产生过渡噪声

格雷码与8421码之间的转换
以 n = 3 为例,8421码与格雷码之间的对应关系如下:
格雷码也是以全0开头的
| 十进制 | 8421码 | 格雷码 |
|---|---|---|
| 0 | 000 | 000 |
| 1 | 001 | 001 |
| 2 | 010 | 011 |
| 3 | 011 | 010 |
| 4 | 100 | 110 |
| 5 | 101 | 111 |
| 6 | 110 | 101 |
| 7 | 111 | 100 |
2.1 8421码 ==> 格雷码
算法 1、8421码最左边一位不变,保留下来成为格雷码的最左边一位; 2、从左边第二位开始,将8421码的每一位与它左边的一位相 异或 得到对应位的格雷码;
代码实现
<span style="background-color:#f8f8f8"><span style="color:#333333">public static int toGrayCode(int i) {
return i ^ (i >> 1);
}</span></span>将 i 与i - 1 异或,也即将 i 的每一位与它的左边一位相异或。右移操作左边是补的0,0与任何数异或等于其本身,因此最左边一位被保留了。
2.2 格雷码 ==> 8421码
算法 1、格雷码的最左边一位保持不变,保留下来成为8421码的最左边一位; 2、从左边第二位开始,将格雷码的每一位与前一位计算得到的8421码 异或 得到当前的8421码;
解释
8421码转格雷码是通过 i ^ (i - 1) 实现的,要想将格雷码转换为8421码,我们知道,异或运算有如下性质: (a ^ b) ^ b = a ^ (b ^ b) = a
因此,可以得到 (i ^ (i >> 1)) ^ (i >> 1) = i ^ ((i >> 1) ^ (i >> 1)) = i 所以在上面的算法中在计算当前位的8421码时,需要将当前位的格雷码与上一位计算得到的8421码异或。
美国信息交换标准代码(ASCII)

知识回顾与重要考点

2.1_3_无符号整数的表示和运算
无符号整数在计算机中的应用

无符号整数的表示


无符号整数的加法运算

无符号整数的减法运算
-
“被减数"不变,"减数"全部位按位取反、末位+1,减法变加法
-
从最低位开始,按位相加,并网更高位进位


知识回顾

2.1_4_带符号整数的表示和运算原反补
带符号整数在计算机中的应用

原码
原码表示

原码的缺点

原码->反码->补码的转换

补码中从右往左找到的第一个1的左边的数和反码保持一致
右边的数和原码保持一致
注意:无论是是原码->反码,还是原码->补码,都是“数值位“按位取反

补码的加法运算
注意:
-
补码数值位不能解读为“位权”
-
符号位参与运算


补码的减法运算
方法一 : 全部位按位取反,末位加1
方法二:补码中找到的第一个1左边的数全部取反(包括符号位)


知识回顾与重点考点

2.1_5_原反补码的特性对比
此处的(最小数/最大数)为补码、反码转回原码后(真值)的(最小值/最大值)
注意:
-
补码的最小值为-2^n
-
补码的真值0只有1种表示方式
-
补码中的-128无法转换为相同位数的原码
-
[1000 0000]作为补码表示-128不是算出来的, 是规定的


2.1_6_移码

移码:补码的基础上将符号位取反
注:移码只能用于表示整数


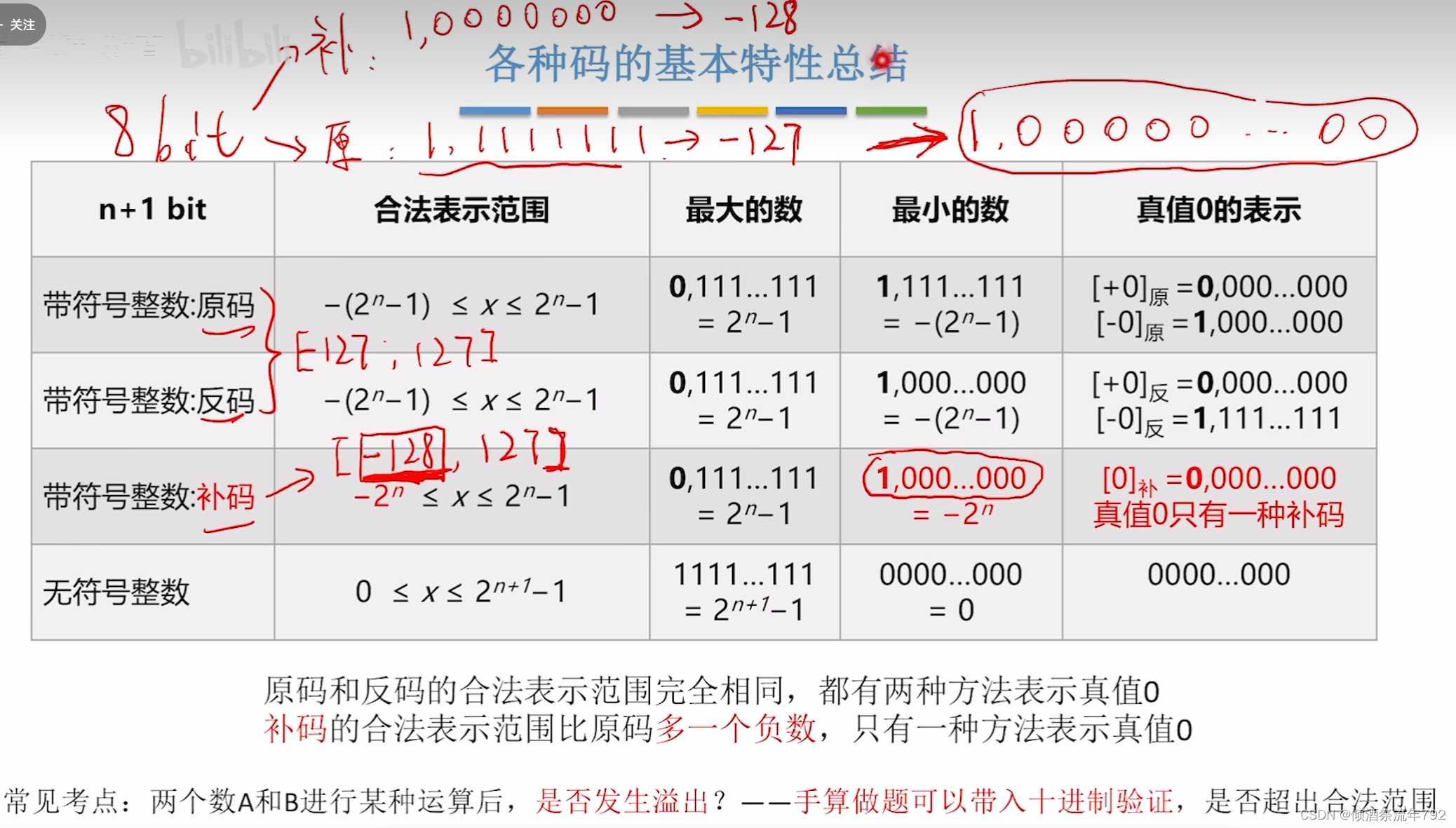
2.1_7_各种码的基本特性总结
总结:
-
原码和反码的真值0有两种表示
-
补码和移码的真值0只有一种表示
-
补码和移码可以多表示一个负数


练习
易错:
-
0代表正数,1代表负数
-
正数的原码、反码、补码相同
移码真值的绝对值 + 补码真值的绝对值 = 128(2^{n - 1}) n为位数

2.1_8_定点小数

原码

原码/反码/补码的转换

定点小数的加/减运算
对两个定点小数A、B进行加法/减法时,需要先转换为补码(与定点整数补码运算法则一致)

定点小数VS定点整数

2.1_9_-128的二进制
负数用它的绝对值的补数表示也就是“模-|负数x|” 表示
把0~255进行对半分,0~127以及128~255像上面所说的100一样,,0~127表示正数,128~255表示负数补数的负值,也就是说128~255为【模】-|负数x|后的值,256-|-128|=128,256-|-1|=255
2.2_0_奇偶校验码


奇数个1,异或结果为1
偶数个1,异或结果为0

2.2_1_电路的基本原理、串行进位加法器设计
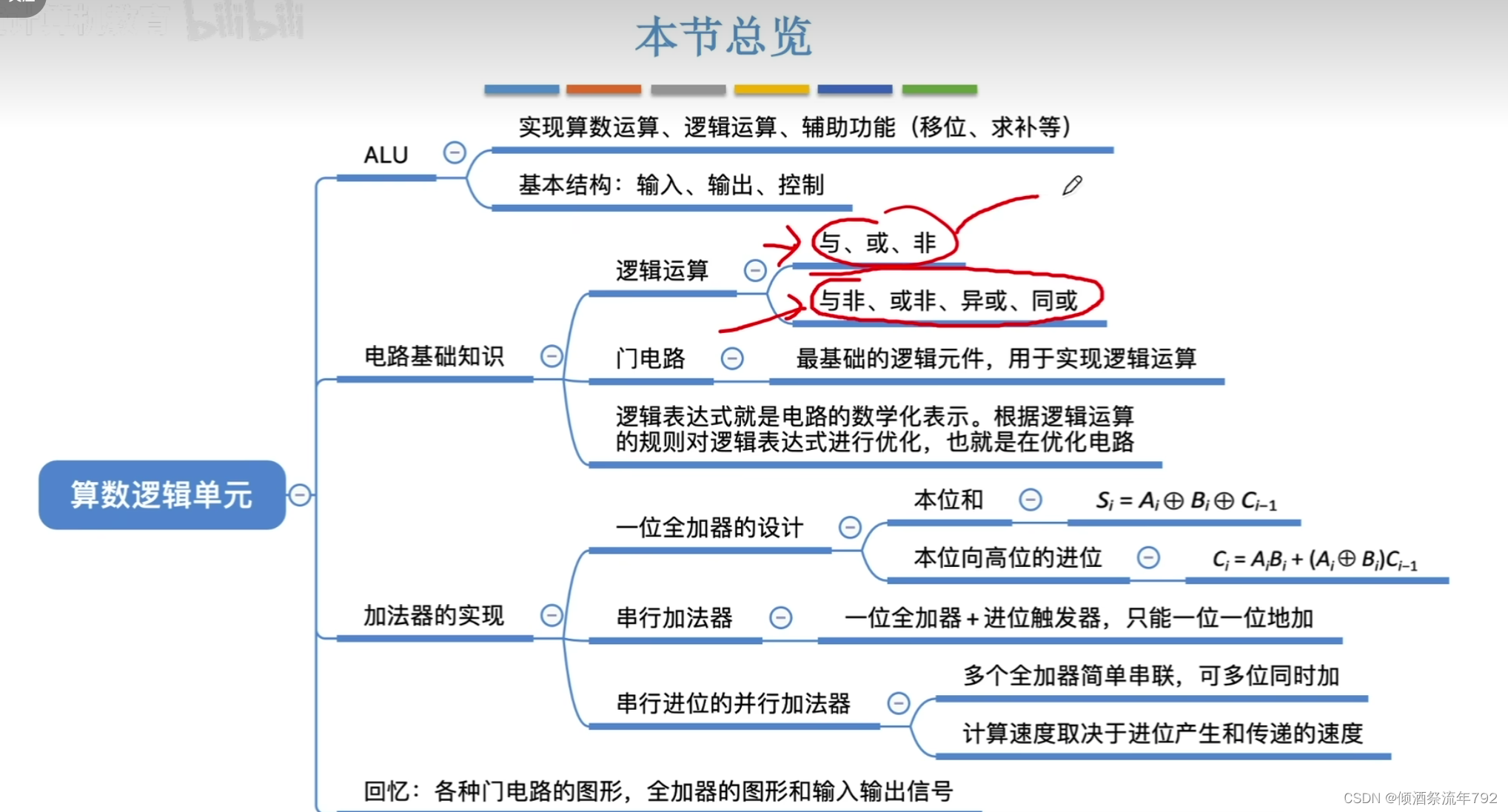
总览

算数逻辑单元ALU
机器字长:计算机能直接处理的二进制数据的位数,机器字长一般等于内部寄存器的大小,它决定了计算机的运算精度。

最基本的逻辑运算

优先级:与 > 或

复合逻辑


用门电路求偶校验位

一位全加器

串行加法器

串行进位的并行加法器

本节总览
2.2_2_并行进位加法器

并行加法器的优化
每一位的进位几乎是同时产生的
-
每一个进位都可以分解为最初已知的数值运算的结果

2.2_3_补码加减运算器
加法器原理
Cin:来自低位的进位
Cout: 最高位产生的进位

补码的加减运算

加法运算:Sub为0,Cin为0
减法运算:Sub为1, Cin为1
Sub = Cin
此处X,Y均为补码
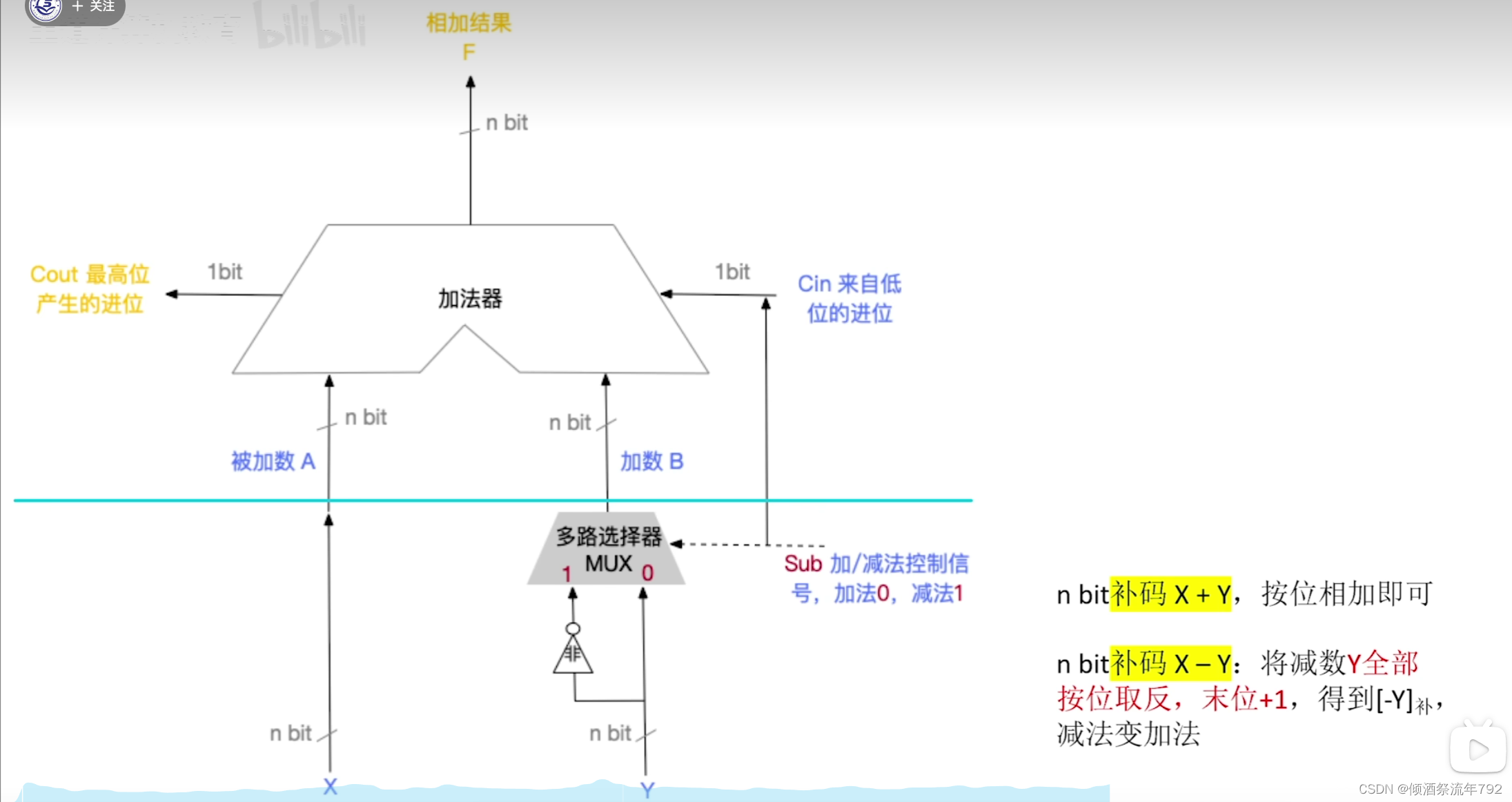
此电路通路适用于无符号整数
无符号整数加法,直接相加
减法,减数全部位按位取反,末位加一,减法变加法

2.2_4_标志位的生成

OF(Overflow flag)
溢出标志位
OF = 最高位产生的进位 & 次高位产生的进位
范围:仅对有符号数有效
含义:有符号数的加减运算是否发生了溢出
本质:判断符号位是否发生改变(即结果的最高位由0变为1或由1变为0)
-
一正一负不会产生溢出
-
两个正数:0(最高位进位)& 1(次高位进位)
例:0100 + 0111 = 1011(溢出)0 -> 1
-
两个负数:1(最高位进位)& 0(次高位进位)
例:1000 + 1100 = 10100(溢出)1 -> 0,4bit,最高位的1舍去
SF(Sign flag)
符号标志位
OF = 最高位的本位和
范围:仅对有符号数有效
含义:有符号加减运算的正负性
ZF(Zero flag)
零标志位
含义:结果是否为0,ZF = 1表示运算结果为0,ZF = 0表示运算结果为1
CF(Carry flag)
进位标志位
CF = 最高位产生的进位 & sub(sub = 1,表示减法,sub = 0,表示加法)
范围:仅对无符号数有效
含义:进位/借位标志
-
加法:只有两个数最高位同为1,产生进位
1000 + 1100 = 10100(进位)
-
减法
-
借位条件:最高位不产生进位(0 & (sub == 1) = 1)
-
X - Y
X + (-Y),可能会产生借位(X < Y)
X = 1011(11) Y = 1100(12)
1011 + 0011 + 1 = 1111(产生借位)
-
2.2_5_定点数的移位运算
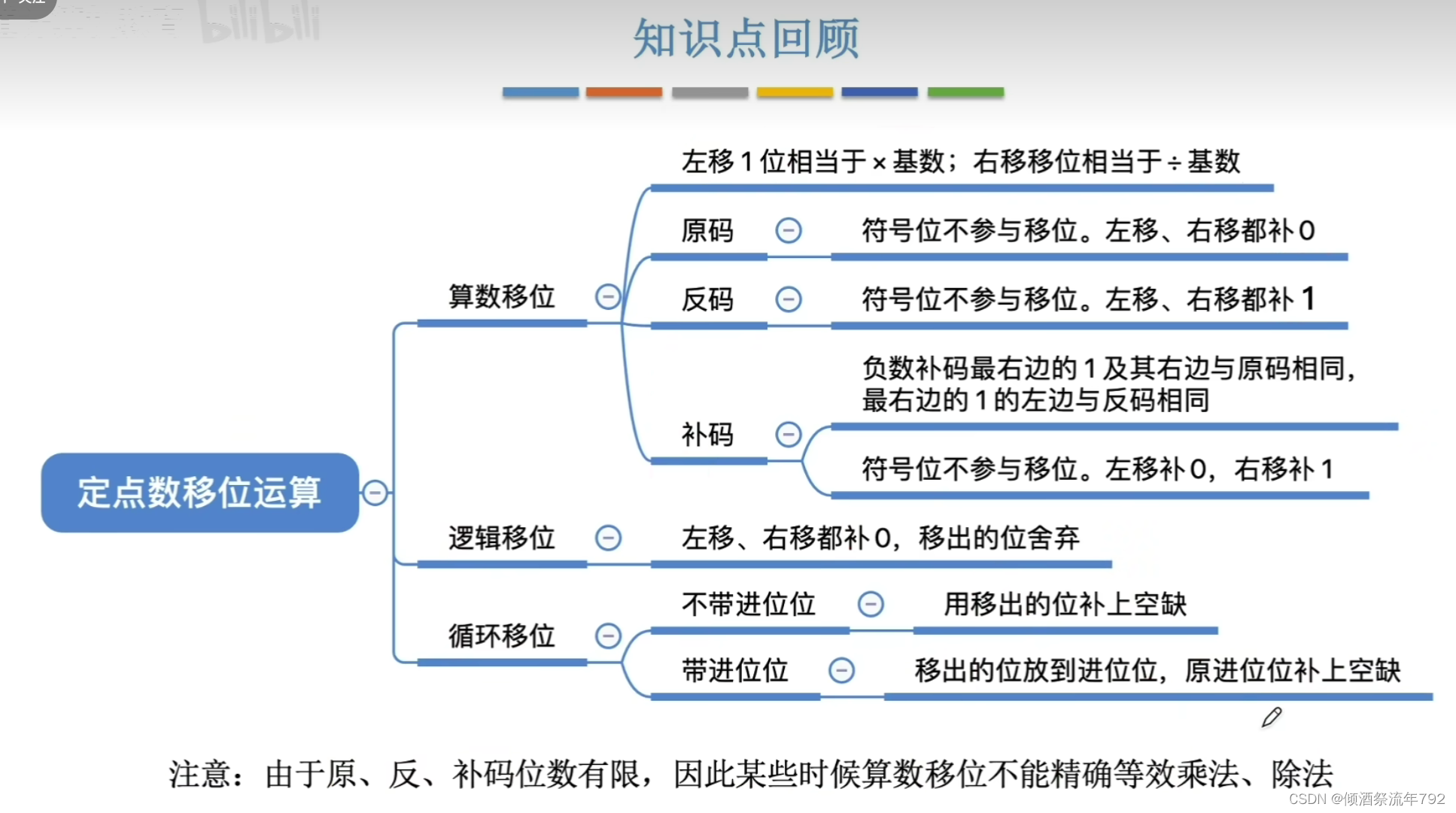
知识总览

算数移位
符号位不参与移位

原码的算数移位


反码的算数移位
正数反码算数移位(同原码):
-
右移(同原码),高位补0,低位舍弃
-
左移(同原码),低位补0, 高位舍弃
负数反码算数移位:
-
右移,高位补1,低位舍弃
-
左移,低位补1, 高位舍弃

补码的算数移位
在补码中,从右往左找到第一个1,这个1的左边与反码保持一致,这个1及右边的数同原码保持一致
正数补码算数移位(同原码):
-
右移(同原码),高位补0,低位舍弃
-
左移(同原码),低位补0, 高位舍弃
负数补码算数移位:
-
右移(同反码),高位补1,低位舍弃
-
左移(同原码),低位补0, 高位舍弃

精度损失

算数移位的应用举例

逻辑移位
符号位参与移位
相当于无符号数的算数移位

逻辑移位的应用举例

循环移位
可以用于高低字节的调换(大小端转换)
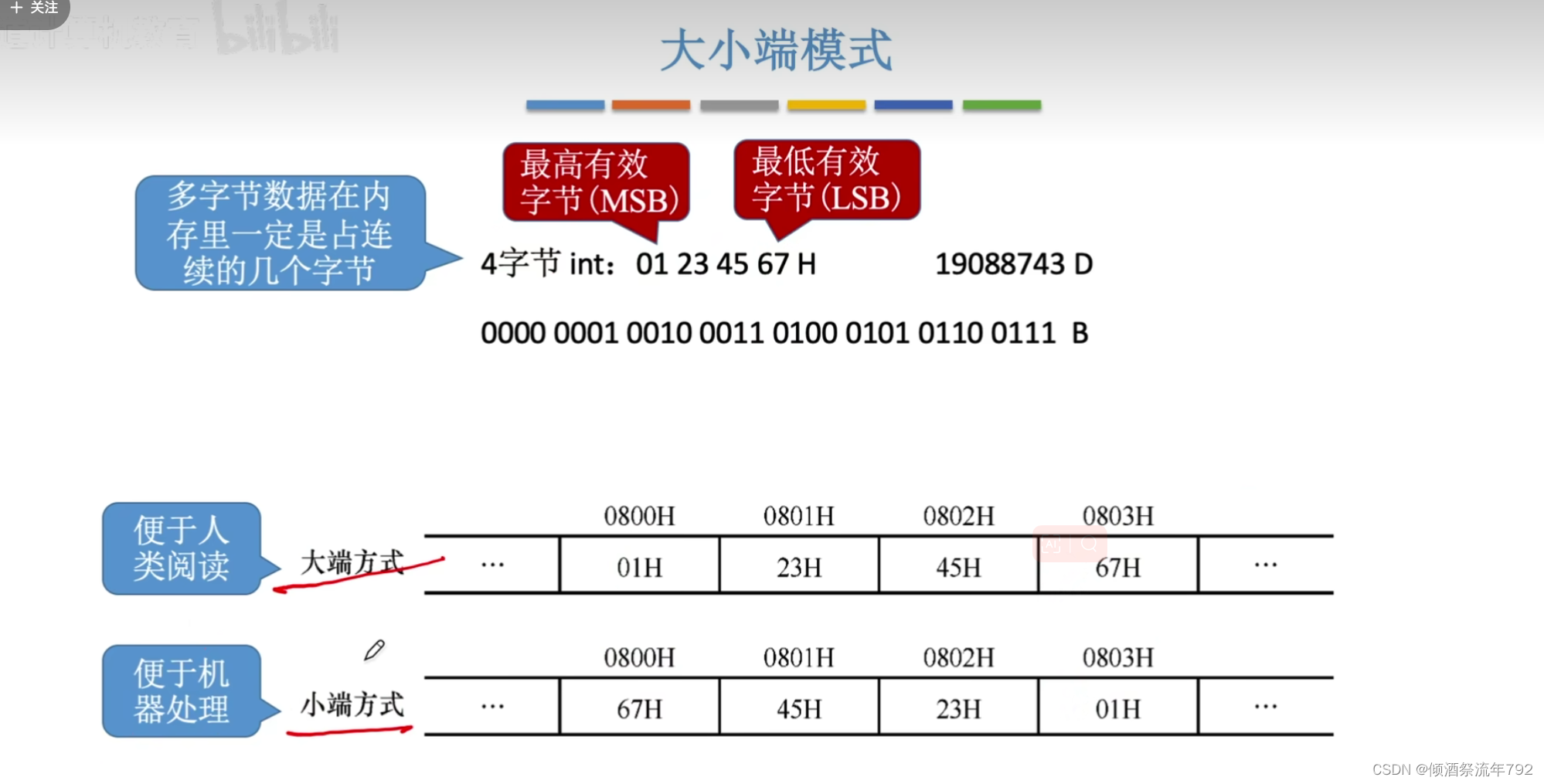
大端:数据的高字节存储在地址的低位,数据的低字节存储在地址的高位(与平时读写一致)
小端:数据的低字节存储在地址的高位,数据的高字节存储在地址的低位

总结
2.2_6_原码补码一位乘法运算
总览

乘法运算的实现思想
手算乘法(十进制)

手算乘法(二进制)

原码一位乘法
符号单独处理:符号位 = x_s^y_s
数值位取绝对值进行乘法计算



红色的数字称为--部分积




手算模拟
Tips:
-
逻辑右移(符号参与移位)
01.0011 右移1位 00.1001 1
-
乘数的符号位不参与运算
-
原码一位乘法可以只用单符号位

补码一位乘法

MQ为单符号位的补码(最后一位为辅助位)
X为双符号位的补码

补码一位乘法(手动模拟)
-
进行4次右移
-
最后还要对补码的MQ的最后一位(原符号位)进行加法运算(不进行右移操作)
注:
-
补码的算数右移(符号位不参与移动)
11.0101
右移 11.1010 1
负数的补码,左移右补0,右移左补1
-
符号位参与运算
11.1011
+ 00.1101
= 100.1000 = 00.1000

2.2_7_原码补码一位除法运算
总览

除法运算的思想



原码除法:恢复余数法
步骤:
-
计算机默认上商1
-
ACC中存入被除数-除数的结果
-
检测到符号位为负数
-
进行改正,商0,ACC加上除数,恢复余数
-
ACC和MQ中所有数逻辑左移,MQ低位补0

上商1(ACC存储的余数为|x| - |y| = |x| + [-|y|_{补码}] )

检测到错误(符号位为1,即被除数 < 除数)

修正(恢复余数,上商0),(ACC存储的余数恢复为 |x| + |y| = |x| + [|y|_{补码}])


逻辑左移

步骤:
-
计算机默认商1
-
ACC中存入被除数-除数的结果
-
检测到符号位为正数,得到正确余数
-
ACC和MQ中所有数逻辑左移,MQ低位补0




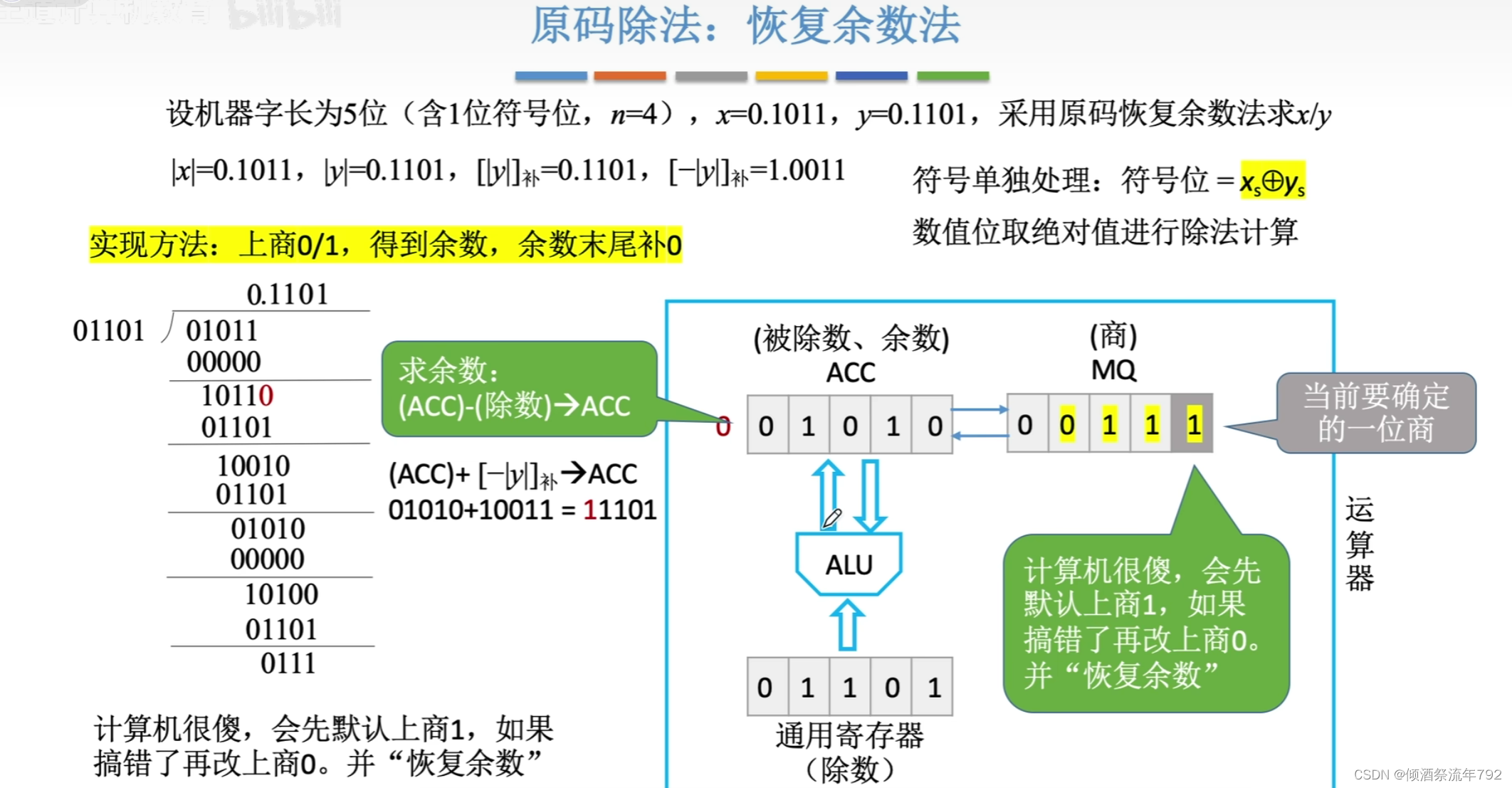

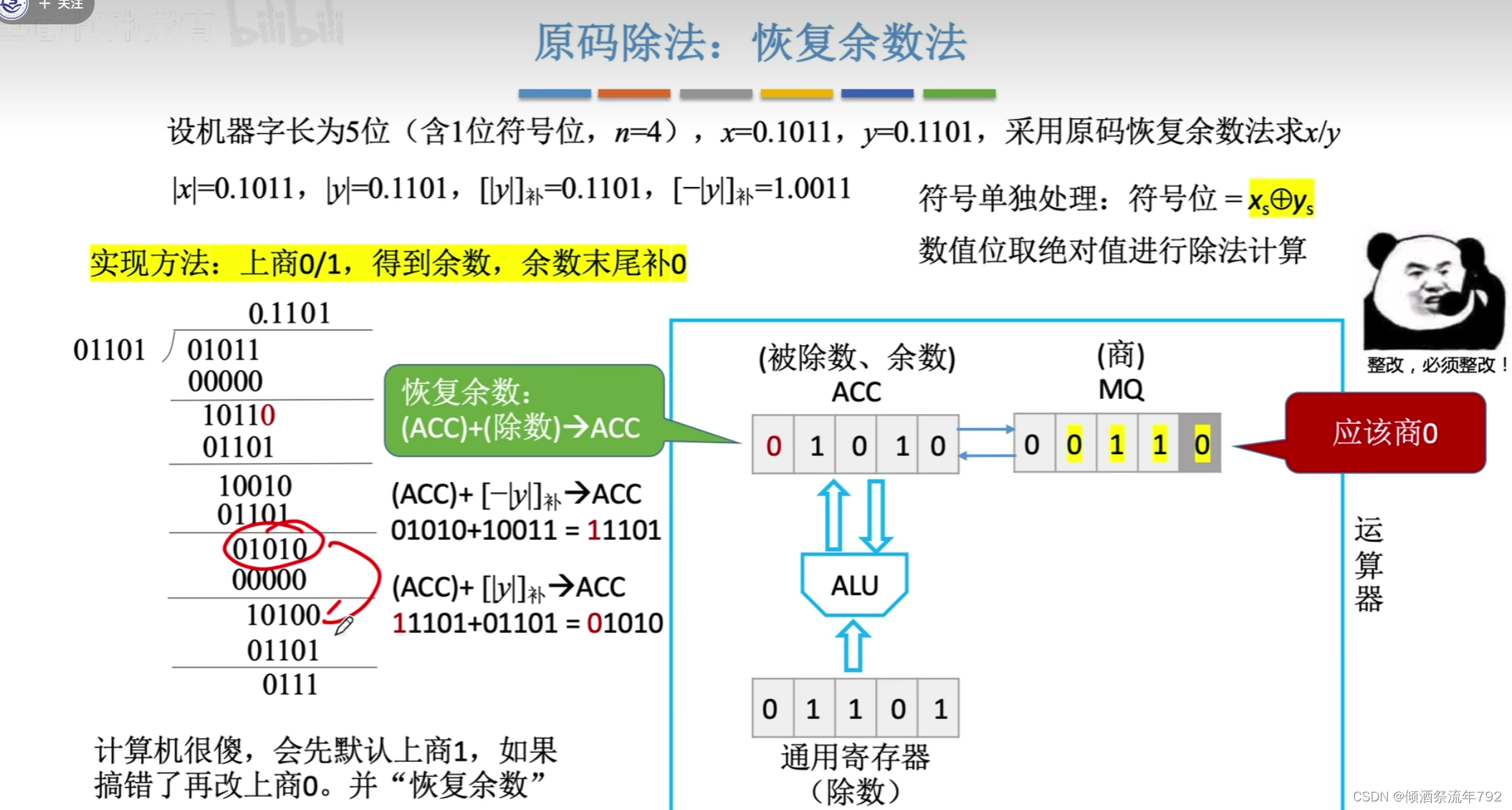



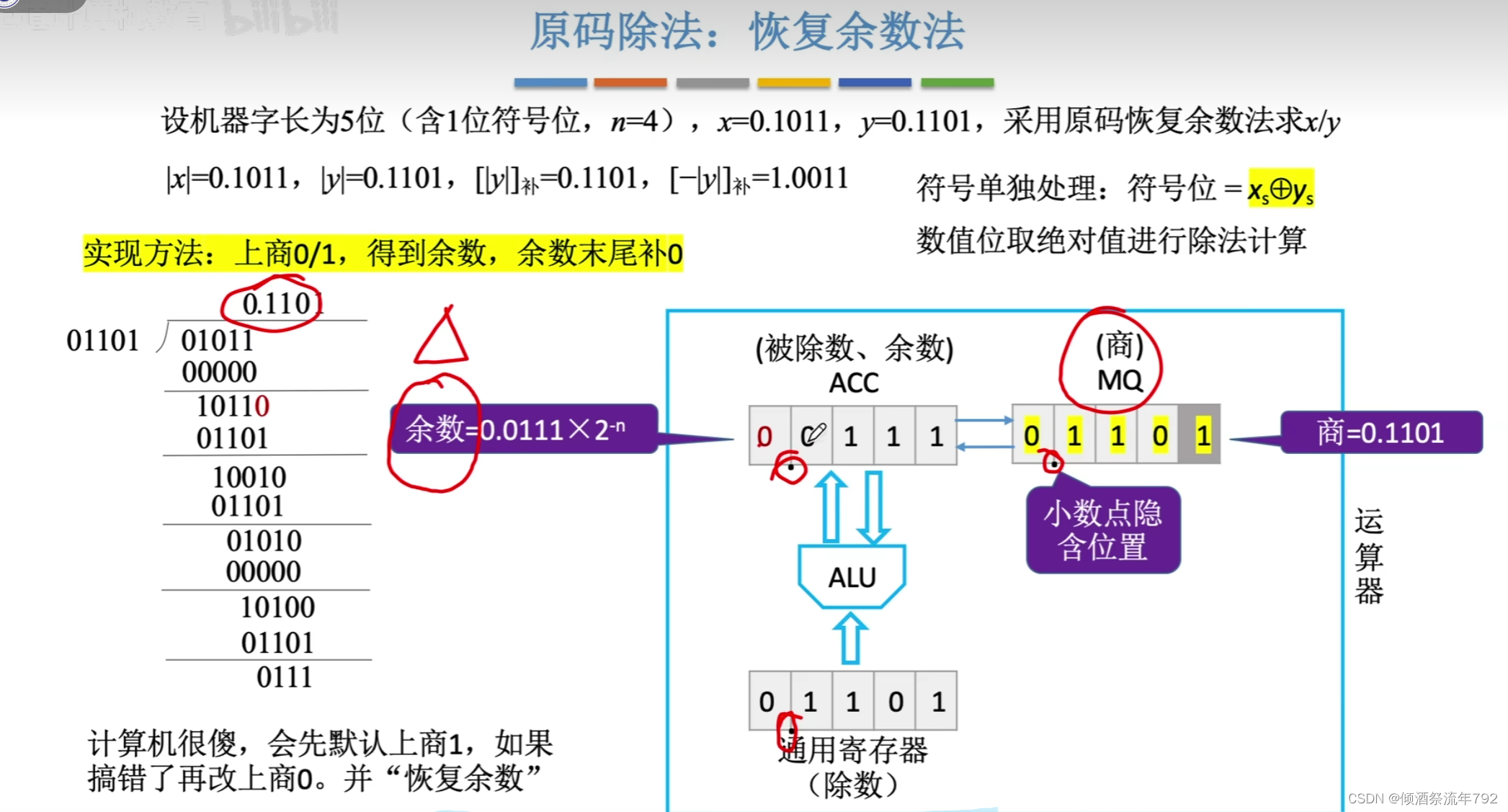
原码除法:恢复余数法(手算)
左移n次,上商n+1次,最后一次上商不进行左移


原码除法:加减交替法


定点小数无法表示>1的数,所以第一次商1,结果一定是负数
否则硬件电路直接停止操作
Tips:若余数为负,需商0,并+[|y|]_补的到正确的余数
补码除法

补码除法:
-
符号位参与运算(此处为[y_{补码}],而不是[-|y|_{补码}])
-
被除数/余数、除数采用双符号位


除法运算总结回顾

2.2_8_C语言类型转换

#include<stdio.h>
int main()
{
// 无符号数变有符号数,不改变数据内容,改变解释方式
// 正数符号位为0,无影响;负数符号位为1,有影响,数据变大
short x = -4321;
unsigned short y = (unsigned short)x;
printf("x = %d, y = %d\n", x, y);
printf("\n");
// 长整数变短整数,高位截断,保留低位(数值改变,正负可能发生改变)
int a = 165537, b = -34991;
short c = (short)a, d = (short)b;
printf("a = %d, c = %d\nc = %d, d = %d\n", a, b, c, d);
printf("\n");
return 0;
}
#include<stdio.h>
int main()
{
// 短整数变长整数,符号扩展,真值不变
short m = -4321;
int n = m;
// 无符号数变有符号数,不改变数据内容,改变解释方式
unsigned short p = (unsigned short)m;
// 无符号数到无符号数的转变(短整型 -> 长整型,未发生溢出),高位补0,真值不变
unsigned int q = (unsigned int)p;
printf("m = %d, n = %d\np = %d, q = %d\n", m, n, p, q);
printf("\n");
// 无符号数到无符号数的转变(发生溢出),结果为0
printf("%d\n", sizeof(unsigned short)); // unsigned short占2个字节,存储的最大值为2^15 - 1 = 65535
unsigned int x = 65535; // unsigned short范围内
unsigned int y = 65536; // unsigned short范围外
unsigned short z1 = (unsigned short)x;
unsigned short z2 = (unsigned short)y; // 短整型—>长整型,溢出,结果为0
printf("x = %d, z1 = %d\ny = %d, z2 = %d\n", x, z1, y, z2);
return 0;
}
2.2_9_数据的存储和排列
大小端模式
边界对齐
计算机(CPU)一次能处理数据的最大位数称为该机器的字长(机器字长)
假设计算机为32位,即存储字长为32,即一个字为32bit
一行为2个半字
一行为1个字
一行为4个字节

下图中
-
如果采用边界不对齐方式,因为CPU每次访存只能访问1个字,所以CPU需要2次访存,耗时较长
-
如果采用边界对齐方式,只需要一次访存,但是会出现“碎片”


2.3_1_浮点数的表示
本节总览

定点数的局限性

从科学计数法理解浮点数

浮点数的表示
阶码:常用补码或移码表示的定点整数
尾数:常用原码或补码表示的顶点小数

a = 0,01;1,1001
-
分号前面为阶码
-
分号后面为尾数
-
逗号前面为正负


浮点数尾数的规格化
无效值:小数点前为0,小数点后第一个数也为0


规格化浮点数的特点

知识回顾

2.3_2_IEEE 754
读音:i triple e 754
移码


IEEE754中阶码用移码表示,偏置值为127(2^{n-1} - 1)
负数真值的绝对值 > 偏置值,进行mod2^8
即:x - y(x < y) = x + 2^8 - y
-1000 0000 + 0111 1111 = -1000 0000 + 0111 1111 + 1 0000 0000 = 1111 1111


IEEE754标准
求阶码的真值方法
-
先把阶码看做无符号数,转为10进制
-
减去偏置值



最大绝对值和最大绝对值
阶码的最小值为-126,全0(-127)和全1(-128)有特殊用途
阶码的最大值为127

阶码全1、全0的特殊用途


知识回顾

2.3_3_浮点数的运算
浮点数的加减运算(十进制)
小阶向大阶对齐
原因:计算机内部,尾数采用定点小数,想让小数点固定在好几位有效值后面,计算机不易处理
例如:985.211*10^{12}

浮点数的加减运算(二进制)

x - y = 11100,10.110001000 -> -1.001111*2^{-100}
需要右移(与双符号位的第一位保持一致),进行规格化,并且阶码+1

浮点数的加减运算-舍入

强制类型转换
64位机器中,long型占64位,double尾数为53位,会发生精度丢失

此处说的精度从小到大转换没有精度损失(32位系统下)
int - > float,会损失精度

float - > int
溢出:float表示范围远大于int
精度损失:float为0.001,转为int,变为了0

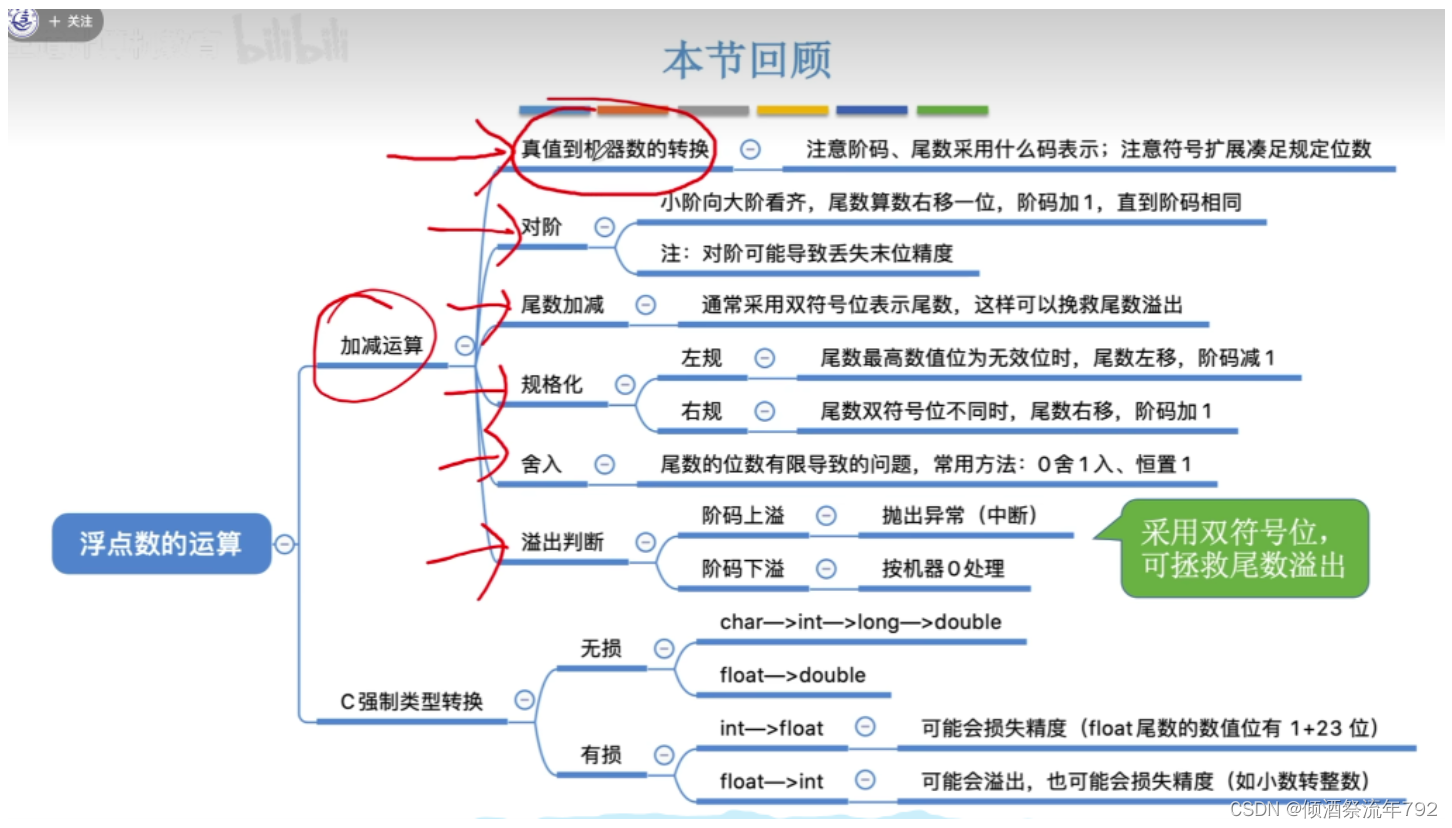
本节回顾























 1643
1643

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








