信号与编码 预习式复习 第二章（2）

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

目录

文章目录

前言

一、信息熵：

1.定义

2.基本性质和定理：

二、条件熵：

1.定义：

2.例题：

三、联合熵：

1.定义：

四、多符号离散平稳信源熵：

1.离散平稳无记忆信源熵：

2.离散平稳有记忆信源熵：

五、例题

总结

---

前言

给出各种熵的图像表达，便于大家理解。该图像也可以带入到自信息量中。 

---

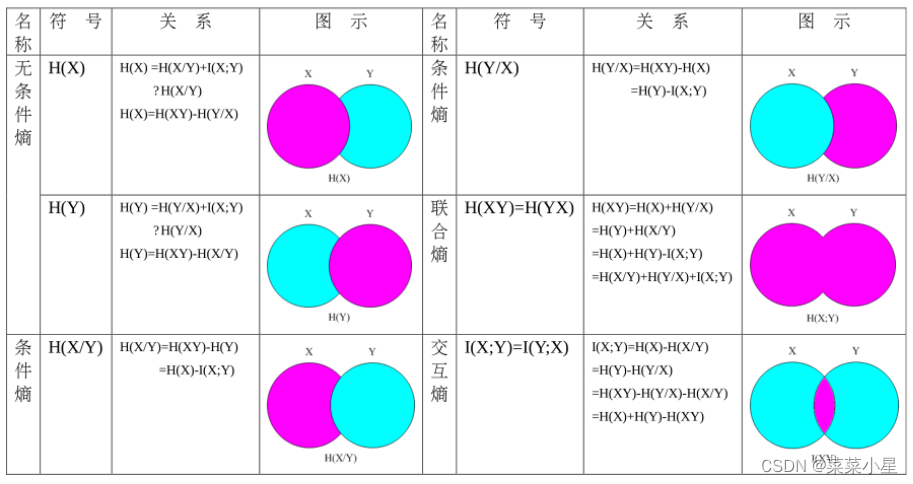
一、信息熵：

1.定义

信源各个离散消息的自信息量的数学期望值就是信源的平均量,一般称为信源的信息熵，又叫信源熵或者香农熵。

即：概率×自信息量之和

①信源熵反映的是输出前平均不确定度的一个大小

②信源熵反应心愿输出后，平均每个离散消息提供的信息量

③反应变量X的随机性

信息熵和平均信息量数值相等，但概念不同。

2.基本性质和定理：

①非负性

②对称性

③最大离散熵定理：信源X中包含n个不同离散消息时，信源熵有：,

当且仅当X中各消息出现的概率全相等时，该式取等号。

即时，最大。

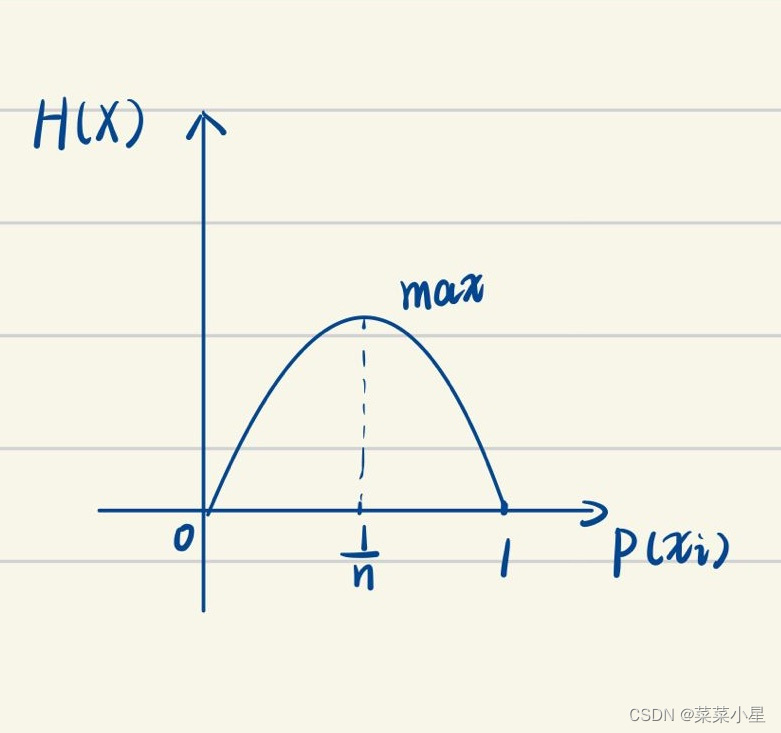
④扩展性

⑤确定性

⑥可加性

⑦极值性：已知Y时X的不确定度应小于对Y一无所知时X的不确定度。即;

同理：

⑧上凸性

二、条件熵：

1.定义：

条件熵时在联合符号XY上的条件自信息量的数学期望。又叫做噪声熵

（记得相加求和，（和）的概率× （和）的自信息量

条件熵是一个确定的值，随N增加是非递增的。

2.例题：

三、联合熵：

1.定义：

联合熵也叫共熵，是脸和离散符号集合XY上元素的脸和自信息量的数学期望。

四、多符号离散平稳信源熵：

1.离散平稳无记忆信源熵：

离散平稳无记忆信源X的N次扩展信源的熵就是单符号离散信源X的熵的N倍，表示为：

2.离散平稳有记忆信源熵：

将离散平稳有记忆信源推广到N维的情况可证明：

以此类推可得到：

大家可以试着动手推一遍，考试时会有证明题出现。

五、例题

1.

 

 2.总结后的自信息量、互信息量和各种信源熵及其关系

 

---

总结

大家可以留意最后放的例题的第二题，找出最适合自己的求解方式，