对于一个字符串 S,我们定义 S 的分值 f(S) 为 S 中出现的不同的字符个数。例如f(“aba”)=2,f(“abc”)=3,f(“aaa”)=1。
现在给定一个字符串S[0...n−1](长度为 n),请你计算对于所有S 的非空子串S[i...j](0≤i≤j<n),f(S[i...j]) 的和是多少。
输入描述
输入一行包含一个由小写字母组成的字符串S。
其中 。
。
输出描述
输出一个整数表示答案。
题解
这道题暴力的求解只能过一半的样例,时间复杂度过高,考虑动态规划。
把S的所有子串按照末尾字符分成n组(n是S的长度)。这样就把S的所有非空子串分成n份,既不会有重复的,也不会遗漏任意一个S的子串。然后针对每一份子串进行讨论。
重新定义一个f[i]。与题目中的f(S)不同。
f[i]指的是由S的第1个字符到S的第i个字符,合计i个字符组成的字符串的一系列子串的分值和(这些子串的末尾一定含有S的第i个字符)。//这里与S的子串定义不一样!!!
可以把这个新的字符串就理解成一个不一样的S,这里可以称此字符串为S2;接下来求解f[i]。
f[i]是S2的所有非空子串的分值和(每个子串一定包括S的第i个字符,即以S的第i个字符结尾)(S2由S的第一个字符到第i个字符组成)。
注意f[i]不是字符串,不是分值,而是分值和。S与S2才是字符串。
要求f[i]就要求f[i]与f[i-1]之间的关系(动态规划常见思路),现在来观察从S的第一个字符到S的第i个字符组成的S2。
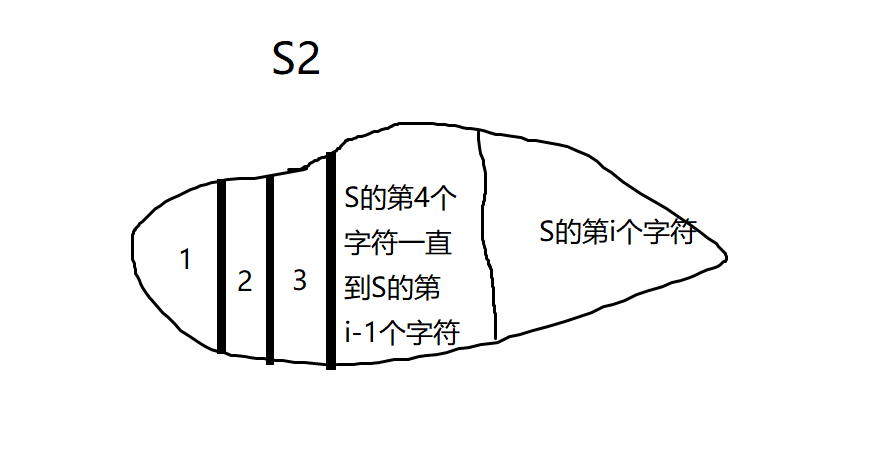
设S2中S的第i个字符为ch,从ch往前面找,设第一个与ch一模一样的字符的位置是pos。
此时假设已知f[i-1](f[i-1]指一定以S的第(i-1)个字符结尾的子串分值和)。
f[i]描述的子串仅比f[i-1]描述的子串多一个ch,那么f[i]=f[i-1]+i-pos。
所以代码中要把第i个字符出现的上一个位置记录下来。
对于第一个字符,出现的上一个位置应当是0。
下面是代码。
#include <bits/stdc++.h>
using namespace std;
int pos[26];
const int N = 1e5 + 10;
int f[N];
int main()
{
char s[N];
cin >> s + 1;
long long ans = 0;
int n = strlen(s + 1);
for (int i = 1; i <=n; ++i)
{
int t = s[i] - 'a';
f[i] = f[i - 1] + i - pos[t];
pos[t] = i;
ans += f[i];
}
printf("%lld",ans);
return 0;
}这道题关键在于按照末尾字符将S分成n份。
经典动态规划。
千里之行,始于足下。







 文章讲述了如何使用动态规划方法解决计算字符串所有非空子串不同字符个数总和的问题。通过按末尾字符将字符串分成组,定义新的f[i]表示以第i个字符结尾的子串分值和,从而找出f[i]与f[i-1]的关系,最终实现高效计算。
文章讲述了如何使用动态规划方法解决计算字符串所有非空子串不同字符个数总和的问题。通过按末尾字符将字符串分成组,定义新的f[i]表示以第i个字符结尾的子串分值和,从而找出f[i]与f[i-1]的关系,最终实现高效计算。
















 362
362

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








