typora中插入LaTeX数学公式
本文内容参考https://blog.youkuaiyun.com/baidu_38060633/article/details/79183905 在Typora上进行了实验。
typora公式语法
数学公式有两种形式: inline 和 display
- **inline(行间公式)?*在正文插入数学公式,用
$...$将公式括起来 - display(快间公式) :独立排列的公式,用
$$...$$将公式括起来,默认显示在行中间
equation是用户给当前公式自定义的名字(随便写)
LaTeX 编辑数学公式基本语法元素
-
各类希腊字母表:
eg:
$\alpha$:α\alphaα
常用语法
所有字符后面都可以跟个空格,避免与表达式中的字母符号混淆
| 特殊字符 | 说 明 | 实例 |
|---|---|---|
| $ | 数学公式前后加$是行内公式 | 数学公式: a = x + y a=x+y a=x+y |
| $$ | 数学公式加$$就是读占一行的公式 | 独占一行: a = x + y a=x+y a=x+y |
| \ | 转义字符,特殊字符要显示原意,就在前面加\ | $$$ |
| \\ | 在数学公式中是换行 | a = x + y b = y a=x+y\\b=y a=x+yb=y |
| _ | 后跟内容为下标 | a i a_i ai |
| ^ | 后跟内容为上标 | a i a^i ai |
| {} | 被括号起来的公式是一组内容 | x 22 y ( x ) x y z x_{22} y^{(x)} x^{y^z} x22y(x)xyz |
| \frac | 分数 | 1 a \frac{1}{a} a1 |
| \sqrt | 根号 | x y + x a \sqrt{xy}+\sqrt[a]{x} xy+ax |
| \ldots | 跟文本底线对齐的省略号 | a i … n a_{i\ldots{n}} ai…n |
| \cdots | 跟文本中线对齐的省略号 | i ⋯ n i\cdots n i⋯n |
| \sum | 求和 | $\sum_{k=1}^nkx $ |
| \int | 积分 | ∫ a b \int_a^b ∫ab |
| \limits | 强制上下限在上下侧 | $\sum\limits_{k=1}^nkx $ |
| \nolimits | 强制上下限在右侧 | ∑ k = 1 n k x \sum\nolimits_{k=1}^nkx ∑k=1nkx |
| \overline | 上划线 | a + b ‾ \overline{a+b} a+b |
| \underline | 下划线 | a + b ‾ \underline{a+b} a+b |
| \overbrace | 上花括号 | a + b + ⋯ + n ⏞ m 个 \overbrace{a+b+\dots+n}^{m个} a+b+⋯+n m个 |
| \underbrace | 下花括号 | a + b + ⋯ + n ⏟ m 个 \underbrace{a+b+\dots+n}_{m个} m个 a+b+⋯+n |
| \vec | 向量 | a ⃗ \vec{a} a |
| \lim | 极限 | lim x → ∞ \lim_{x \to \infty} limx→∞ |
| \left \right | 用于自适应匹配分隔符如{,(, | 详情见方程组 |
| \approx | 约等于 | ≈ \approx ≈ |
| \cdot | 点乘 | A ⋅ B A\cdot B A⋅B |
| \times | 叉乘 | 5 × 7 5\times7 5×7 |
| \sim | 波浪号 | ∼ \sim ∼ |
Latex的各种帽子
\hat{A}
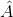
\widehat{A}

\tilde{A}

\widetilde{A}
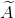
\overline{A}

\underline{A}

\overbrace{A}

\underbrace{A}

\overset{a}{b}

\underset{a}{b}
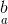
\overleftarrow{A}

\overrightarrow{A}

其他常见例子
注意使用\begin{equation}…\end{equation},equation对应每种表达式,但是单行的情况下可以不用
-
基本预算符: ± \pm ± ÷ \div ÷
-
矩阵与行列式
$$
\begin{matrix}
1 & x & x^2\\
1 & y & y^2\\
1 & z & z^2\\
\end{matrix1}
$$
1 x x 2 1 y y 2 1 z z 2 \begin{matrix} 1 & x & x^2\\ 1 & y & y^2\\ 1 & z & z^2\\ \end{matrix} 111xyzx2y2z2
行列式:
$$
X=\left|
\begin{matrix}
x_{11} & x_{12} & \cdots & x_{1d}\\
x_{21} & x_{22} & \cdots & x_{2d}\\
\vdots & \vdots & \ddots & \vdots \\
x_{11} & x_{12} & \cdots & x_{1d}\\
\end{matrix}
\right|
$$
X = ∣ x 11 x 12 ⋯ x 1 d x 21 x 22 ⋯ x 2 d ⋮ ⋮ ⋱ ⋮ x 11 x 12 ⋯ x 1 d ∣ X=\left| \begin{matrix} x_{11} & x_{12} & \cdots & x_{1d}\\ x_{21} & x_{22} & \cdots & x_{2d}\\ \vdots & \vdots & \ddots & \vdots \\ x_{11} & x_{12} & \cdots & x_{1d}\\ \end{matrix} \right| X=∣∣∣∣∣∣∣∣∣x11x21⋮x11x12x22⋮x12⋯⋯⋱⋯x1dx2d⋮x1d∣∣∣∣∣∣∣∣∣
- 分隔符
各种括号用 () [] { } \langle\rangle 等命令表示,注意花括号通常用来输入命令和环境的参数,所以在数学公式中它们前面要加 \。可以在上述分隔符前面加 \big \Big \bigg \Bigg 等命令来调整大小。
- 箭头
$\leftarrow$
← \leftarrow ←

-
方程式
E=mc^2E = m c 2 E=mc^2 E=mc2
-
分段函数
$$ f(n)= \begin{cases} n/2, & \text{if $n$ is even}\\ 3n+1,& \text{if $n$ is odd} \end{cases} $$f ( n ) = { n / 2 , if n is even 3 n + 1 , if n is odd f(n)= \begin{cases} n/2, & \text{if $n$ is even}\\ 3n+1,& \text{if $n$ is odd} \end{cases} f(n)={n/2,3n+1,if n is evenif n is odd
-
方程组
$$ \left\{ \begin{array}{c} a_1x+b_1y+c_1z=d_1\\ a_2x+b_2y+c_2z=d_2\\ a_3x+b_3y+c_3z=d_3 \end{array} \right. $${ a 1 x + b 1 y + c 1 z = d 1 a 2 x + b 2 y + c 2 z = d 2 a 3 x + b 3 y + c 3 z = d 3 \left\{ \begin{array}{c} a_1x+b_1y+c_1z=d_1\\ a_2x+b_2y+c_2z=d_2\\ a_3x+b_3y+c_3z=d_3 \end{array} \right. ⎩⎨⎧a1x+b1y+c1z=d1a2x+b2y+c2z=d2a3x+b3y+c3z=d3
常用公式
-
线性模型
$$ h(\theta) = \sum_{j=0} ^n \theta_j x_j $$
h ( θ ) = ∑ j = 0 n θ j x j h(\theta) = \sum_{j=0} ^n \theta_j x_j h(θ)=j=0∑nθjxj
-
均方误差
$$ J(\theta) = \frac{1}{2m}\sum_{i=0}^m(y^i - h_\theta(x^i))^2 $$J ( θ ) = 1 2 m ∑ i = 0 m ( y i − h θ ( x i ) ) 2 J(\theta) = \frac{1}{2m}\sum_{i=0}^m(y^i - h_\theta(x^i))^2 J(θ)=2m1i=0∑m(yi−hθ(xi))2
求积公式
$$ H_c=\sum_{l_1+\dots +l_p}\prod^p_{i=1} \binom{n_i}{l_i} $$
H c = ∑ l 1 + ⋯ + l p ∏ i = 1 p ( n i l i ) H_c=\sum_{l_1+\dots +l_p}\prod^p_{i=1} \binom{n_i}{l_i} Hc=l1+⋯+lp∑i=1∏p(lini)
-
批量梯度下降
$$ \frac{\partial J(\theta)}{\partial\theta_j} = -\frac1m\sum_{i=0}^m(y^i - h_\theta(x^i))x^i_j $$∂ J ( θ ) ∂ θ j = − 1 m ∑ i = 0 m ( y i − h θ ( x i ) ) x j i \frac{\partial J(\theta)}{\partial\theta_j} = -\frac1m\sum_{i=0}^m(y^i - h_\theta(x^i))x^i_j ∂θj∂J(θ)=−m1i=0∑m(yi−hθ(xi))xji
-
推导过程
$$ \begin{align} \frac{\partial J(\theta)}{\partial\theta_j} & = -\frac1m\sum_{i=0}^m(y^i - h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(y^i-h_\theta(x^i))\\ & = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(\sum_{j=0}^n\theta_j x^i_j-y^i)\\ &=-\frac1m\sum_{i=0}^m(y^i -h_\theta(x^i)) x^i_j \end{align} $$KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \frac{\partia…
-
字符下标
$$ \max \limits_{a<x<b}\{f(x)\} $$
max a < x < b { f ( x ) } \max \limits_{a<x<b}\{f(x)\} a<x<bmax{f(x)}
参考
- https://blog.youkuaiyun.com/baidu_38060633/article/details/79183905
- https://www.latex-project.org/help/
注:如有问题,请指正,谢谢
^n\theta_j xi_j-yi)\
&=-\frac1m\sum_{i=0}m(yi -h_\theta(x^i)) x^i_j
\end{align}
$$
-
字符下标
$$ \max \limits_{a<x<b}\{f(x)\} $$
max a < x < b { f ( x ) } \max \limits_{a<x<b}\{f(x)\} a<x<bmax{f(x)}
参考
- https://blog.youkuaiyun.com/baidu_38060633/article/details/79183905
- https://www.latex-project.org/help/
注:如有问题,请指正,谢谢
























 3176
3176

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








