力扣70.爬楼梯

题目：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例一：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例二：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

• 1 <= n <= 45

思路：我们有两种方法来实现这道题目，第一种是通过递归的方式，第二种是通过动态数组的方式

方法一：递归

递归记得要写结束条件不然结束无限递归，递归前进的状态就是递归函数调用自己的过程，回退的时候计算结果，前进的时候只是为了找到最底层的递归

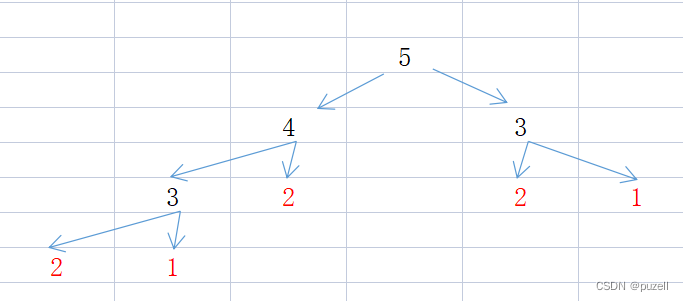
前进的过程当中加号后面的递归并不会进行，只有回退当中加号前面的递归已经彻底结束，值已经返回了，才会去进行加号后面的递归

class Solution {
public:
    int climbStairs(int n) {
        if(n == 1){
            return 1;//递归的回退条件
        }
        if(n == 2){
            return 2;//递归的回退条件
        }
        return climbStairs(n - 1) + climbStairs(n - 2);
    }
};

 

 方法二：动态数组

当我们看上面的过程时，会发现递归当中有很多重复的递归，所以我们使用一个动态数组来解决这个问题。因为到达每一块楼梯的方法就是到达前一块和前两块的方法之和。

class Solution {
public:
    int climbStairs(int n) {
        if(n == 1){
            return 1;
        }
        vector<int> vec(n + 1);
        vec[0] = 1;
        vec[1] = 1;
        for(int i = 2; i < vec.size(); i++){
            vec[i] = vec[i - 1] + vec[i - 2];
        }
        return vec[n];
    }
};

我们也可以对上面的动态数组方法进行优化，我们可以只创建含有三个元素的动态数组，然后再接下来的循环当中，奇数楼梯的方法存放进vec[1],偶数楼梯的方法存放进vec[2]，这样，1可以省去一些空间，在最后返回时也需要考虑n的奇偶性来选择返回哪个数据 

class Solution {
public:
    int climbStairs(int n) {
        if(n == 1){
            return 1;
        }
        vector<int> vec(3);
        vec[1] = 1;
        vec[2] = 2;
       if(n <= 2){
           return vec[n];
       }
       for(int i = 3; i <= n; i++){
           if(i % 2){//判断次数的楼梯数位奇数或偶数
                vec[1] = vec[1] + vec[2];
           }
           else{
               vec[2] = vec[1] + vec[2];
           }
       }
        return n % 2 ? vec[1] : vec[2];
    }
};