本文介绍了如何使用ABY框架进行安全多方计算，包括安装依赖、运行示例程序以及解决编译问题。实验内容涉及安全内积计算和百万富翁比较的实现，通过结合两者并处理判断语句，展示了ABY框架在保护隐私数据的同时进行计算的能力。
两方安全计算实验
一、实验要求
二、ABY框架搭建
ABY框架是一个安全多方计算(Secure Multi-Party Computation, SMPC)的开源框架，它可以用于在不暴露私密数据的情况下协同计算结果。它允许使用混合协议的安全双方计算协议，允许双方在敏感数据上评估函数，同时保护这些数据的隐私。这些协议被表示为算术或布尔电路，可以使用算术共享、布尔共享（GMW协议）或姚氏乱码电路进行私有评估。
1、安装依赖项
sudo apt-get update
sudo apt-get install build-essential cmake libgmp3-dev libssl-dev git
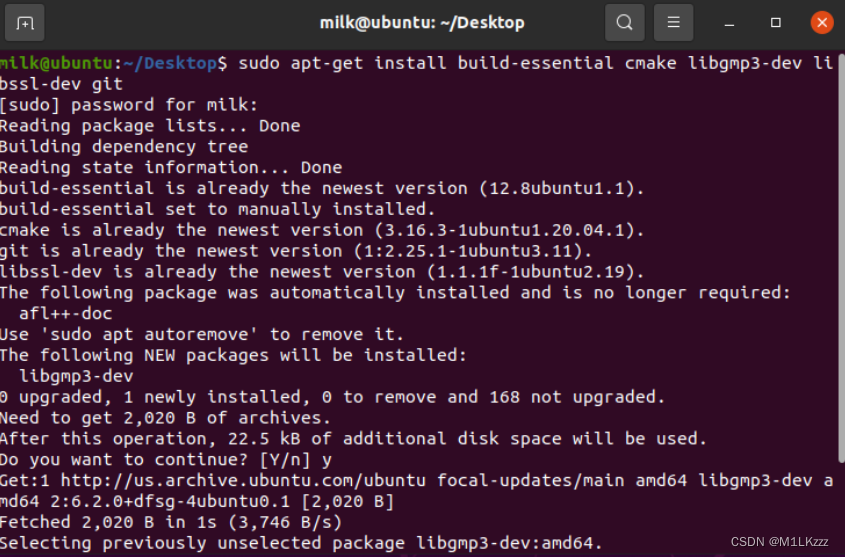
2、克隆ABY仓库
git clone https://github.com/encryptogroup/ABY.git
cd ABY
也可以直接从github上下载解压，获得源码即可。
3、编译和安装ABY
mkdir build
cd build
cmake .. -DABY_BUILD_EXE=On
make -j4
这里在安装过程出现了一些问题后续说明，假设未出现问题，正常运行结果如下
4、运行ABY示例程序
在ABY的examples目录中有多个示例程序。例如，使用加法协议计算两个秘密整数的和：
cd bin
在bin目录下打开两个终端，分别运行下述命令
./millionaire_prob_test -r 0
./millionaire_prob_test -r 1
5、遇到的问题
提示缺少ENCRYPTO_utils和OTExtension
解决方法：通过clone或者下载将OTExtension与ENCRYPTO_utils放入ABY/extern中，后续提示ENCRYPTO_utils缺少relic依赖，同样方法，将其放入ENCRYPTO_utils/extern中即可。
三、实验内容
本次实验的主要内容为两方安全内积计算的实现、百万富翁比较的实现以及将二者进行连通后对判断语句进行处理。
两方安全内积的实现可参考ABY框架所给示例innerproduct_test.cpp：
//Utility libs
#include <ENCRYPTO_utils/crypto/crypto.h>
#include <ENCRYPTO_utils/parse_options.h>
//ABY Party class
#include "../../abycore/aby/abyparty.h"
#include "common/innerproduct.h"
int32_t read_test_options(int32_t* argcp, char*** argvp, e_role* role,
uint32_t* bitlen, uint32_t* numbers, uint32_t* secparam, std::string* address,
uint16_t* port, int32_t* test_op) {
uint32_t int_role = 0, int_port = 0;
parsing_ctx options[] =
{ { (void*) &int_role, T_NUM, "r", "Role: 0/1", true, false },
{ (void*) numbers, T_NUM, "n", "Number of elements for inner product, default: 128", false, false },
{ (void*) bitlen, T_NUM, "b", "Bit-length, default 16", false, false },
{ (void*) secparam, T_NUM, "s", "Symmetric Security Bits, default: 128", false, false },
{ (void*) address, T_STR, "a", "IP-address, default: localhost", false, false },
{ (void*) &int_port, T_NUM, "p", "Port, default: 7766", false, false },
{ (void*) test_op, T_NUM, "t", "Single test (leave out for all operations), default: off",
false, false } };
if (!parse_options(argcp, argvp, options,
sizeof(options) / sizeof(parsing_ctx))) {
print_usage(*argvp[0], options, sizeof(options) / sizeof(parsing_ctx));
std::cout << "Exiting" << std::endl;
exit(0);
}
assert(int_role < 2);
*role = (e_role) int_role;
if (int_port != 0) {
assert(int_port < 1 << (sizeof(uint16_t) * 8));
*port = (uint16_t) int_port;
}
return 1;
}
int main(int argc, char** argv) {
e_role role;
uint32_t bitlen = 16, numbers = 128, secparam = 128, nthreads = 1;
uint16_t port = 7766;
std::string address = "127.0.0.1";
int32_t test_op = -1;
e_mt_gen_alg mt_alg = MT_OT;
read_test_options(&argc, &argv, &role, &bitlen, &numbers, &secparam, &address, &port, &test_op);
seclvl seclvl = get_sec_lvl(secparam);
// call inner product routine. set size with cmd-parameter -n <size>
test_inner_product_circuit(role, address, port, seclvl, numbers, bitlen, nthreads, mt_alg, S_ARITH);
return 0;
}
百万富翁比较的实现可参考框架所给示例millionaire_prob_test.cpp：
//Utility libs
#include <ENCRYPTO_utils/crypto/crypto.h>
#include <ENCRYPTO_utils/parse_options.h>
//ABY Party class
#include "../../abycore/aby/abyparty.h"
#include "common/millionaire_prob.h"
int32_t read_test_options(int32_t* argcp, char*** argvp, e_role* role,
uint32_t* bitlen, uint32_t* nvals, uint32_t* secparam, std::string* address,
uint16_t* port, int32_t* test_op) {
uint32_t int_role = 0, int_port = 0;
parsing_ctx options[] =
{ { (void*) &int_role, T_NUM, "r", "Role: 0/1", true, false }, {
(void*) nvals, T_NUM, "n",
"Number of parallel operation elements", false, false }, {
(void*) bitlen, T_NUM, "b", "Bit-length, default 32", false,
false }, { (void*) secparam, T_NUM, "s",
"Symmetric Security Bits, default: 128", false, false }, {
(void*) address, T_STR, "a",
"IP-address, default: localhost", false, false }, {
(void*) &int_port, T_NUM, "p", "Port, default: 7766", false,
false }, { (void*) test_op, T_NUM, "t",
"Single test (leave out for all operations), default: off",
false, false } };
if (!parse_options(argcp, argvp, options,
sizeof(options) / sizeof(parsing_ctx))) {
print_usage(*argvp[0], options, sizeof(options) / sizeof(parsing_ctx));
std::cout << "Exiting" << std::endl;
exit(0);
}
assert(int_role < 2);
*role = (e_role) int_role;
if (int_port != 0) {
assert(int_port < 1 << (sizeof(uint16_t) * 8));
*port = (uint16_t) int_port;
}
//delete options;
return 1;
}
int main(int argc, char** argv) {
e_role role;
uint32_t bitlen = 32, nvals = 31, secparam = 128, nthreads = 1;
uint16_t port = 7766;
std::string address = "127.0.0.1";
int32_t test_op = -1;
e_mt_gen_alg mt_alg = MT_OT;
read_test_options(&argc, &argv, &role, &bitlen, &nvals, &secparam, &address,
&port, &test_op);
seclvl seclvl = get_sec_lvl(secparam);
//evaluate the millionaires circuit using Yao
test_millionaire_prob_circuit(role, address, port, seclvl, 32,
nthreads, mt_alg, S_YAO);
//evaluate the millionaires circuit using GMW
//test_millionaire_prob_circuit(role, address, port, seclvl, 32,
// nthreads, mt_alg, S_BOOL);
return 0;
}
结合上述代码，将两方安全内积计算与百万富翁比较结合起来后，再将两者连通并处理给定判断语句，具体代码实现如下：
#include <ENCRYPTO_utils/crypto/crypto.h>
#include <ENCRYPTO_utils/parse_options.h>
#include <abycore/circuit/circuit.h>
#include <abycore/aby/abyparty.h>
#include <abycore/sharing/sharing.h>
#include <iostream>
int32_t main(int32_t argc, char** argv) {
e_role role;
uint32_t bitlength = 32;
parse_party_and_port(argv, argc, &role, nullptr);
ABYParty* party = new ABYParty(role, "localhost", 7766);
Circuit* circ = party->getCircuit();
Sharing* shar = party->getSharing();
std::vector<uint32_t> X = shar->get_random_vec_uint32(4);
std::vector<uint32_t> A = shar->get_random_vec_uint32(4);
std::vector<uint32_t> Y = shar->get_random_vec_uint32(4);
std::vector<uint32_t> B = shar->get_random_vec_uint32(4);
std::vector<Sharing*>& shares_X = shar->share(X);
std::vector<Sharing*>& shares_A = shar->share(A);
std::vector<Sharing*>& shares_Y = shar->share(Y);
std::vector<Sharing*>& shares_B = shar->share(B);
std::vector<Sharing*> prod_XY(shares_X.size(), nullptr);
std::vector<Sharing*> prod_AB(shares_A.size(), nullptr);
for (size_t i = 0; i < shares_X.size(); ++i) {
prod_XY[i] = circ->PutMULGate(shares_X[i], shares_Y[i]);
prod_AB[i] = circ->PutMULGate(shares_A[i], shares_B[i]);
}
Sharing* inner_prod_XY = shar->Reconstruct(circ->PutADDGate(prod_XY));
Sharing* inner_prod_AB = shar->Reconstruct(circ->PutADDGate(prod_AB));
Sharing* cmp = shar->A2BGreaterThanBEQZ(inner_prod_XY, inner_prod_AB);
uint32_t res_XY, res_AB, res_cmp;
party->ExecCircuit();
shar->reveal(&res_XY, inner_prod_XY);
shar->reveal(&res_AB, inner_prod_AB);
shar->reveal(&res_cmp, cmp);
std::cout << "X: " << X[0] << ", " << X[1] << ", " << X[2] << ", " << X[3] << std::endl;
std::cout << "A: " << A[0] << ", " << A[1] << ", " << A[2] << ", " << A[3] << std::endl;
std::cout << "Y: " << Y[0] << ", " << Y[1] << ", " << Y[2] << ", " << Y[3] << std::endl;
std::cout << "B: " << B[0] << ", " << B[1] << ", " << B[2] << ", " << B[3] << std::endl;
std::cout << "Inner product of X and Y: " << res_XY << std::endl;
std::cout << "Inner product of A and B: " << res_AB << std::endl;
std::cout << "The larger of the two inner products: " << ((res_cmp == 1) ? res_XY : res_AB) << std::endl;
delete party;
return 0;
}
整体来看，在这个代码中，我们使用四维随机向量，首先生成两个随机向量X和A，并将它们与随机向量Y和B一起分别分享给Alice和Bob。然后，我们使用ABY框架的电路计算方法计算内积X和Y的内积、A和B的内积，并比较这两个内积，找出最大的内积。最后，将结果输出到控制台并进行清理。
在ABY框架中，我们使用ABYParty类来创建Alice和Bob的实例，并使用getCircuit方法获取一个Circuit对象。该电路对象代表了一个空的电路，在其中可以添加网关并定义输入和输出。ABYParty还提供了getSharing方法，用于在共享模式下操作数据。共享模式是一种安全计算模式，其中每个参与方只知道共享值的一部分，需要与其他参与方协作才能重构出完整的值。
然后，使用PutMULGate方法将对应元素相乘，然后使用PutADDGate方法将它们相加，以计算两个向量的内积。最后，使用Reconstruct方法将结果分享回明文，并使用A2BGreaterThanBEQZ方法比较两个内积，找到最大的内积。
在执行电路时，我们使用ExecCircuit方法来计算电路并重建结果，然后使用reveal方法将结果分享回明文，并将其输出到控制台。
运行结果如下：
可以看到两个实例都打印了相同的输出结果，这表明它们成功地执行了内积计算，并通过ABY框架进行安全通信。
四、总结感想
通过本次实验，对安全内积计算、百万富翁比较有了更加深刻的理解，同时，学习了ABY框架的一些基本使用方法，并且在一步步的尝试试错过程中，对安全多方计算的理解也越来越深刻。
扫一扫
476
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
