在
基于法向量朝向的点云语义分割https://mp.youkuaiyun.com/mp_blog/creation/editor/125392432
一文中我们已经能够划分出我们想要的朝向的近似平面点云了

在前文中,我们划分朝向如图,只有三个主轴。在某些朝向有规则的点云模型里,如规则六面体点云,规则八面体点云。这种方法是明显不适用的。与全是平滑曲面的不规则兔子点云不同。我们不可能花费大量的时间去寻找这些近似平面的法向量主轴。

现有一个单层的点云集,观察得到其中有许多法向量朝向相似的近似平面点云。为减少人工寻找主轴方向的复杂工作,现在需要基于自适应法向量朝向进行点云语义分割。

主成成分分析
主成分分析的主要目的是希望用较少的变量去解释原来资料中的大部分变异,将我们手中许多相关性很高的变量转化成彼此相互独立或不相关的变量。
照前文处理流程进行法向量估计,在本方案中我们取法向量在球面的映射点云

根据主成成分分析的思想,要想获得这些近似平面的朝向,我们所需要的应该是朝向相似的密集法向量区域

通过观察可以大致分割为这四个主成成分区域,但是右侧的俩个高密度区连在一起,姑且吧他们看做单一成分,如下图。

这样,即可通过高密度聚类将向量投影划分为三块主成成分区域。
逻辑流
导入待处理的点云,法向量估计。
开始聚类,在法向量映射图像上根据需要调整密度大小,筛选出密度的集中区。
各个簇计算质心向量(主轴)。
根据聚类索引找出单层点云中各个类的点,分组染色。
完整代码
import open3d as o3d
import numpy as np
import matplotlib.pyplot as plt
pcd = o3d.io.read_point_cloud("..\pcd.pcd")
pcd1 = pcd
pcd2 = pcd
pcd.paint_uniform_color([0.5, 0.5, 0.5])
pcd.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=1, max_nn=30))
pcd.orient_normals_consistent_tangent_plane(8)
normal_point = o3d.utility.Vector3dVector(pcd.normals)
normals = o3d.geometry.PointCloud()
normals.points = normal_point
pcd = normals
labels = np.array(pcd.cluster_dbscan(eps=0.1,min_points=230,print_progress=False))
max_label = labels.max()
colors = plt.get_cmap("tab20")(labels / (max_label if max_label > 0 else 1))
print(colors)
colors[labels < 0] = 0
pcd.colors = o3d.utility.Vector3dVector(colors[:, :3])
pcd1.colors = o3d.utility.Vector3dVector(colors[:, :3])
o3d.visualization.draw_geometries([pcd1], window_name="点云密度聚类",
height=480, width=600,
mesh_show_back_face=0) 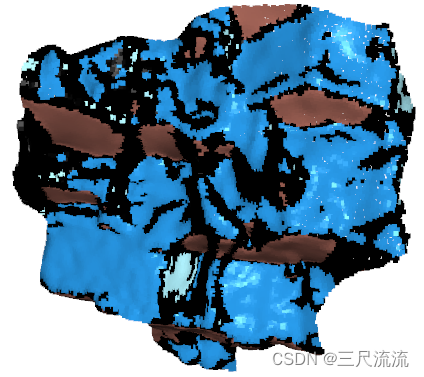



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










