前缀和和差分以及练习题目

蓝桥杯备赛系列

倒计时50天！

前缀和和差分

知识点

前缀和数组：
假设原数组用a[i]表示，前缀和数组用sum[i]表示，那么sum[i]表示的是原数组前i项之和，注意一般用前缀和数组时，原数组a[i]的有效下标是从1开始的。式子如下，
$$sum[n]=\sum _{i=1}^{n}a[i]$$
差分数组：
假设原数组用a[i]表示，差分数组用d[i]表示，那么d[i]表示的是a[i]和a[i-1]之差，注意一般用差分数组时，原数组a[i]的有效下标也是从1开始的。式子如下，
$$d[n]=a[i]-a[i-1]$$
接下来看一下前缀和和差分的模板题。

前缀和模板

题目描述

给定一个长度为$n$的数组$a_1,a_2,....a_n.$

接下来有$q$次查询, 每次查询有两个参数$l,r$.

对于每个询问, 请输出$a_l+a_{l+1}+...+a_r.$

输入描述

第一行包含两个整数$n$和$q$.

第二行包含n个整数, 表示$a_1,a_2,....a_n.$

接下来q行,每行包含两个整数 l和r.

$1\le n,q\le 10^5$
$-10^9\le a[i]\le 10^9$
$1\le l\le r\le n$

输出描述

输出$q$行,每行代表一次查询的结果.

样例输入

3 2
1 2 4
1 2
2 3

样例输出

3
6

题目分析

前缀和最经典的一个作用就是以O（1）的时间复杂度求区间和。

sum[l-1]=a[1]+a[2]+a[3]+…+a[l-1]

sum[r]=a[1]+a[2]+a[3]+…+a[l-1]+a[l]+…+a[r]

sum[r]-sum[l-1]=a[1]+a[2]+a[3]+…+a[l-1]+a[l]+…+a[r]-(a[1]+a[2]+a[3]+…+a[l-1])

​ =a[l]+a[l+1]+…+a[r]

所以区间[l,r]的和可以用sum[r]-sum[l-1]表示。

题目代码

import java.util.Scanner;
public class Main{
   
public static void main(String[] args) {
   
	Scanner scanner = new Scanner(System.in);
	int n = scanner.nextInt();
	int q = scanner.nextInt();
	int a[] = new int[n+1];
	long sum[] = new long[n+1];
	for(int i = 1;i <= n;i++) a[i] = scanner.nextInt();
	for(int i = 1;i <= n;i++) sum[i] = sum[i-1] + a[i];
	while(q-- > 0) {
   
		int l = scanner.nextInt();
		int r = scanner.nextInt();
		System.out.println(sum[r]-sum[l-1]);
	}
}
}

二维前缀和模板

题目描述

给你一个 n 行 m 列的矩阵 A ，下标从1开始。

接下来有 q 次查询，每次查询输入 4 个参数 $x1,y1,x2,y2$

请输出以 $(x1,y1)$为左上角 ,$ (x2,y2)$ 为右下角的子矩阵的和，

输入描述

第一行包含三个整数n,m,q.

接下来n行，每行m个整数，代表矩阵的元素

接下来q行，每行4个整数$x1,y1,x2,y2$，分别代表这次查询的参数

$1\le n,m\le 1000$
$1\le q\le 10^5$
$-10^9\le a[i][j]\le 10^9$
$1\le x1\le x2\le n$
$1\le y1\le y2\le m$

输出描述

输出q行，每行表示查询结果。

样例输入

3 4 3
1 2 3 4
3 2 1 0
1 5 7 8
1 1 2 2
1 1 3 3
1 2 3 4

样例输出

8
25
32

题目分析

首先要了解二维前缀和数组的定义，$sum[i][j]$表示的是对左上角行列分别为1，1，右下角行列分别为i，j的矩阵求和。$sum[7][7]$如下图，为红色圈起来的矩阵。注意这里矩阵的下标都是从1开始的。

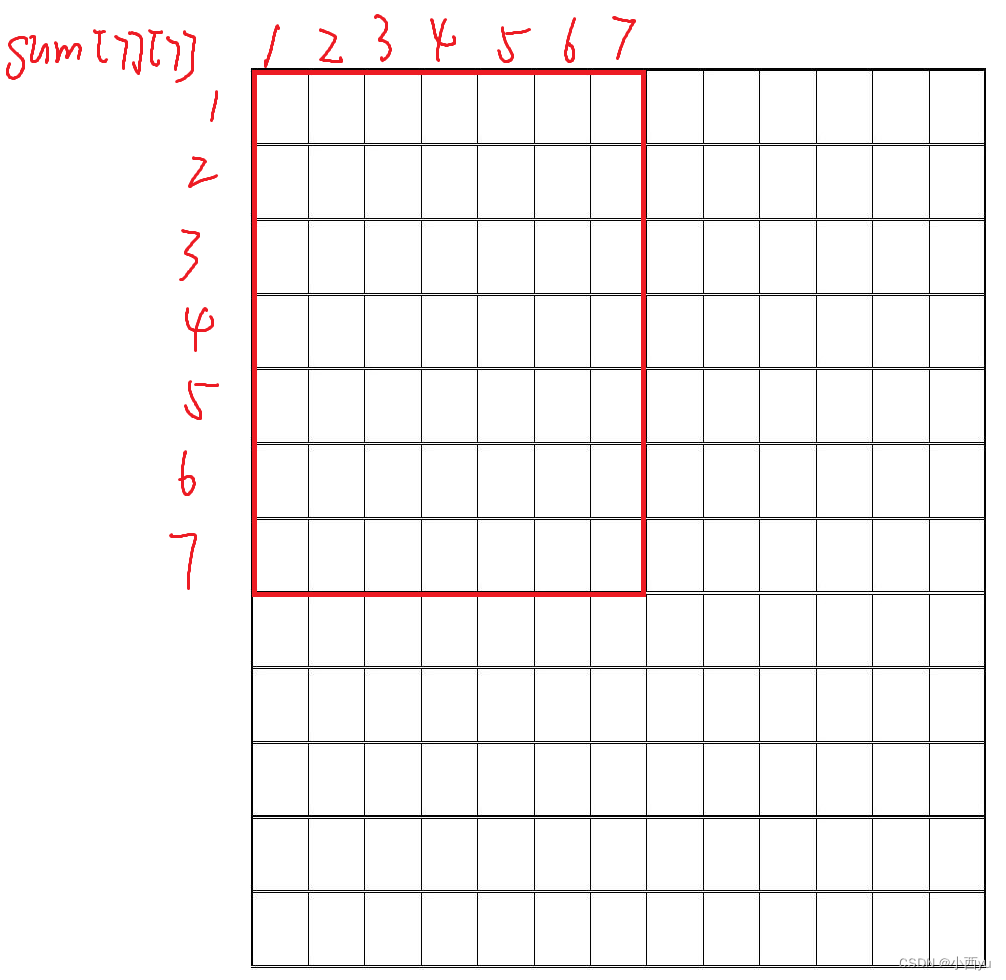
我们通过图片分析如何求二维前缀和数组以及如何利用二维前缀和数组求矩阵和。

如何求二维前缀和数组。如图所示，假设要求$sum[x1][y1]$的值，也就是图中大红色圈起来的部分，我们可以将蓝色部分加上绿色部分后再加上x1,y1处本来的值，也就是$sum[x1][y1-1]+sum[x1-1][y1]+a[x1][y1]$。但是这样会多加上一部分，也就是蓝色和绿色重叠的部分，他用 s u m [ x 1 − 1 ] [ y 1 − 1 ] sum[x1-1][y1-1] sum[x1−1][y1−</