蓝桥杯——算法训练（1，2，3）

如果对您的学习有帮助，请点个赞，在蓝桥杯比赛前，我会努力更新的。

1回形取数

问题描述
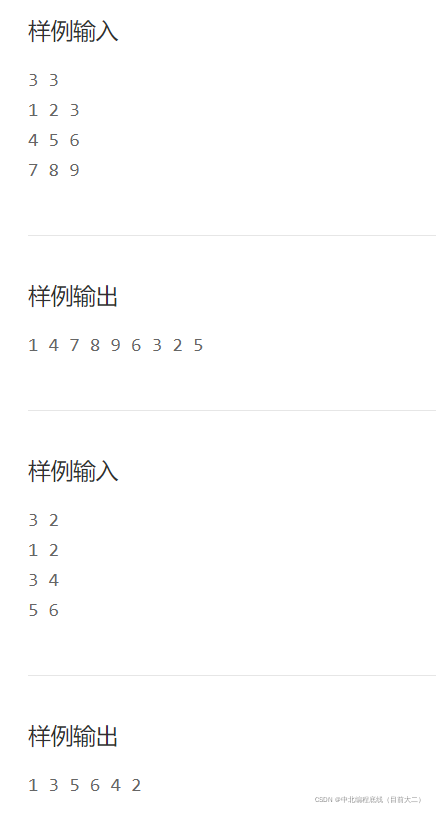
　　回形取数就是沿矩阵的边取数，若当前方向上无数可取或已经取过，则左转90度。一开始位于矩阵左上角，方向向下。
输入格式
　　输入第一行是两个不超过200的正整数m, n，表示矩阵的行和列。接下来m行每行n个整数，表示这个矩阵。
输出格式
　　输出只有一行，共mn个数，为输入矩阵回形取数得到的结果。数之间用一个空格分隔，行末不要有多余的空格。
　　

#include<iostream>
#include<string>
using namespace std;
int a = 0;//读数方向 0下，1右，2上，3左
int num = 1;//拐弯次数
int m=0, n=0;
int m1 = 0, m2 = 0;
int select(int p3)//p1,p2代表坐标，p3代表方向
{
	switch (p3)
	{
	case 0:
		if ((m1 + 1) > (m - num / 4-1))
			{
				m2++;
				num++;
				return 1;
			} 
		  else
			{
			m1++;
			return 0;
			}
		break;
	case 1:
		if ((m2 + 1) > (n - num / 4-1)) 
			{
			m1--;
			num++;
			return 2;
			} 
		else 
			{
			m2++;
			return 1;
			}
		break;
	case 2:
		if ((m1 - 1) <(num / 4)) 
			{
			m2--;
			num++;
			return 3;
			}
		else
			{
			m1--;
			return 2;
			}
		break;
	case 3:
		if ((m2 - 1) <(num / 4)) 
			{
			m1++;
			num++;
			return 0;
			} 
		else
			{
			m2--;
			return 3;
			}
		break;
	}
}
int main()
{
	
	int b[200][200] = {0};
	cin >> m >> n;
	for (int i = 0; i < m; i++)
	{
		for (int j = 0; j < n; j++)
		{
			cin >> b[i][j];
		}
	}
	//输入完毕，开始输出
	for (int k = 0; k < m * n; k++)
	{
		
		switch (a)
		{
		case 0:cout << b[m1][m2]; break;
		case 1:cout << b[m1][m2]; break;
		case 2:cout << b[m1][m2]; break;
		case 3:cout << b[m1][m2]; break;
		}
		a = select(a);
		if (k + 1 < m * n)
			cout << ' ';
	}
	return 0;
}

注意string里面的字符用阿斯克吗记录，没法转换成字符。别在这浪费时间

2试题 算法训练 印章

问题描述
　　共有n种图案的印章，每种图案的出现概率相同。小A买了m张印章，求小A集齐n种印章的概率。
输入格式
　　一行两个正整数n和m
输出格式
　　一个实数P表示答案，保留4位小数。
样例输入
2 3
样例输出
0.7500
数据规模和约定
　　1≤n，m≤20

#include <iostream>
#include <cmath>
#include<iomanip>
using namespace std;
double dp[25][25], p;
int main()
{
	int n, m;
	cin >> n >> m;
	p = 1.0 / n; //每种出现的概率

	for (int i = 1; i <= m; ++i) {
		for (int j = 1; j <= n; ++j) {
			if (i < j) dp[i][j] = 0;
			if (j == 1) {
				dp[i][j] = pow(p, i - 1);  //p^(i-1)
			}
			else {
				dp[i][j] = dp[i - 1][j] * (j * 1.0 / n) + dp[i - 1][j - 1] * ((n - j + 1) * 1.0 / n);
			}
		}
	}
	cout << fixed << setprecision(4) << dp[m][n];
	return 0;
}

这道题是一道动态规划，我们可以用dp来解答；
首先，为了不混乱，我们要记住这么一句话，买i件凑j种。千万记住这句话，要不然一会思维就混乱了。

首先先记住，i是买的数量，j是要凑齐的种类数，这里的i和j不是m和n，m和n是我们求解问题的终点，i和j是中间值，千万别混了，这里是新手禁忌
我们用表格，表格坐标就是（i，j），表格内的值就是概率。
总共有n种，那么我们每一种的概率就是个1/n。
思路如下：
1，首先考虑特殊情况，买一件，i=1，那么如果j=1，概率是1
2，如果买的比要凑齐的种类数少，概率一定是0，即i<j，概率是0
3，如果要凑齐的概率是1，那么概率就是(（1/n）ⁱ)×n即（1/n）^(i-1)这就和第一种合并了（思路就是这么想的）
4，该考虑一般情况了，dp问题就是通过前几个已知的状态来推导现在，dp[i][j]可以由两个前状态推导，
第一个是dp[i-1][j]:就是说前买了前i-1个已经凑齐j种了，那么我们最后一个是以及出现j种中的任意一种都行，即dp[i-1][j]×（1/n）×j
第二个是dp[i-1][j-1]：就是说前i-1个已经凑了j-种，那么最后一种必须和前j-1种不一样，即dp[i-1][j-1]×（1/n）×（n-（j-1））.
完成，收获颇丰

3，试题 算法训练 拿金币

问题描述
　　有一个N x N的方格,每一个格子都有一些金币,只要站在格子里就能拿到里面的金币。你站在最左上角的格子里,每次可以从一个格子走到它右边或下边的格子里。请问如何走才能拿到最多的金币。
输入格式
　　第一行输入一个正整数n。
　　以下n行描述该方格。金币数保证是不超过1000的正整数。
输出格式
　　最多能拿金币数量。
样例输入
3
1 3 3
2 2 2
3 1 2
样例输出
11
数据规模和约定
　　n<=1000

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010;
int m[N][N], sum = 0;
int main() {
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> m[i][j];//输入值
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			//比较上一行的和上一列的求和值：a[i-1][j]+a[i][j],a[i][j-1]+a[i][j]
			m[i][j] = max(m[i][j] + m[i - 1][j], m[i][j - 1] + m[i][j]);
		}
	}

	cout << m[n][n];//输出末尾值

	return 0;
}

这道题没什么说的，就是局部变量里面申请的数组没有全局变量申请的数组空间大。真牛马。卡了半天，收获颇丰啊。

试题 算法训练 数字游戏

问题描述
　　给定一个1～N的排列a[i]，每次将相邻两个数相加，得到新序列，再对新序列重复这样的操作，显然每次得到的序列都比上一次的序列长度少1，最终只剩一个数字。
　　例如:
　　3 1 2 4
　　4 3 6
　　7 9
　　16
　　现在如果知道N和最后得到的数字sum，请求出最初序列a[i]，为1～N的一个排列。若有多种答案，则输出字典序最小的那一个。数据保证有解。
输入格式
　　第1行为两个正整数n，sum
输出格式
　　一个1～N的一个排列
样例输入
4 16
样例输出
3 1 2 4
数据规模和约定
　　0<n<=10

这道题有点意思，想了一会，动笔写了一下，发现了规律。
首先，把从1到10所有情况列出来，

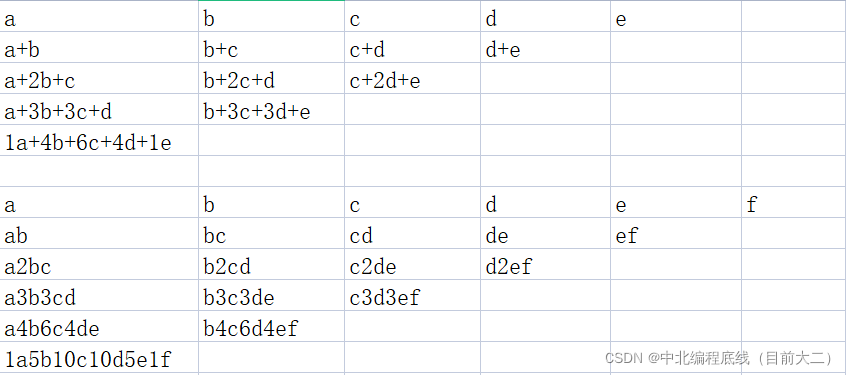
abcdef代表位置
有这个规律
1
11
121
1331
14641
其实就是错位相加差11倍。杨辉三角

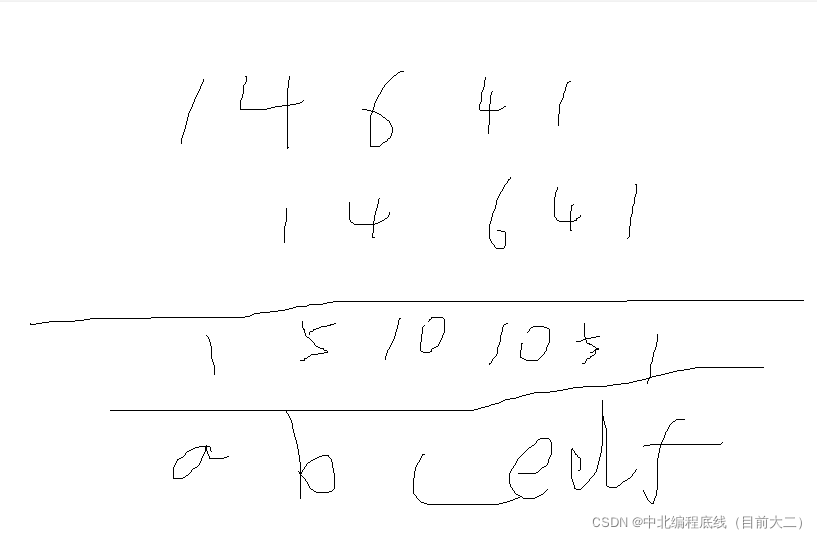
有了这个规律，我们便不用每次都套循环来看每一个字典序的大小了，只需要求出所有字典序然后对应位置相乘就可以了。

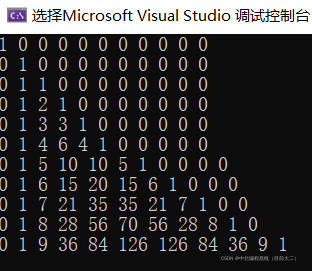
先把杨辉三角写出来，再用一个以为数组记录。

#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
	int a[11][11] = {1};
	int arry[11] = { 0,1,2,3,4,5,6,7,8,9,10 };
	int c[11] = { 0 };
	int i,j,m, n,num=0;
	cin >> m>>n;//4,16
	for (i = 1; i < 11; i++) {		
		a[i][i] = 1;
		a[i][1] = 1;
	}
	for (i = 3; i < 11; i++)
		for (j = 2; j <= i - 1; j++) 
			a[i][j] = a[i - 1][j - 1] + a[i - 1][j];
	for (int k = 1; k <= m; k++)
	{
		c[k] = a[m][k];
	}
	do
	{
		for (int k = 1; k <= m; k++)
			num = num + c[k] * arry[k];

		if (num == n)
		{
			for (int k = 1; k <= m; k++)
			{
				cout << arry[k] << ' ';
			}
			break;
		}
		else {
			num = 0;
		}
	} while (next_permutation(arry+1, arry + m+1 ));
	return 0;
}

这里用到了next_permutation函数，就是一个algorithm库的函数，用来全排列的，感兴趣去查一下。
想了一上午，干净又卫生啊，兄弟们。