基于并行思想的简单算法优化(最值，排序）

_坐看云起时_

已于 2022-10-17 19:57:46 修改

阅读量1.6k

点赞数 2

分类专栏：数据结构与算法文章标签：开发语言性能优化算法

于 2022-09-22 21:39:56 首次发布

本文链接：https://blog.youkuaiyun.com/qq_53162179/article/details/126959515

版权

数据结构与算法专栏收录该内容

4 篇文章

订阅专栏

并行算法(Parallel Algorithm)是计算机科学中一门单独的分支，由于本人水平有限，时间有限，只大致了解了并行算法的基本模型以及几个常见算法的优化改进，下面以（1）求序列最大值（2）归并排序两个问题做并行处理。

一.求最大值问题

Problem: Finding the largest entry in a list of n numbers.

算法1：

FindMax

Input: L:数组名；n(n>=1):数组元素数量
Output: max:数组中元素的最大值

max:=L[1];
for index:=2 to n do
  if max<L[index] then
      max:=L[index]
  end {if};
end{for}

因为要经过n-1次的比较，所以算法复杂度为O(n)

算法2：

锦标赛方法(Tournament Method)

在该方法中，元素被分对，进行一轮一轮的比较，每一轮都有元素被淘汰，都有元素晋级，等待着下一轮的比较，可以以一棵树来表示：

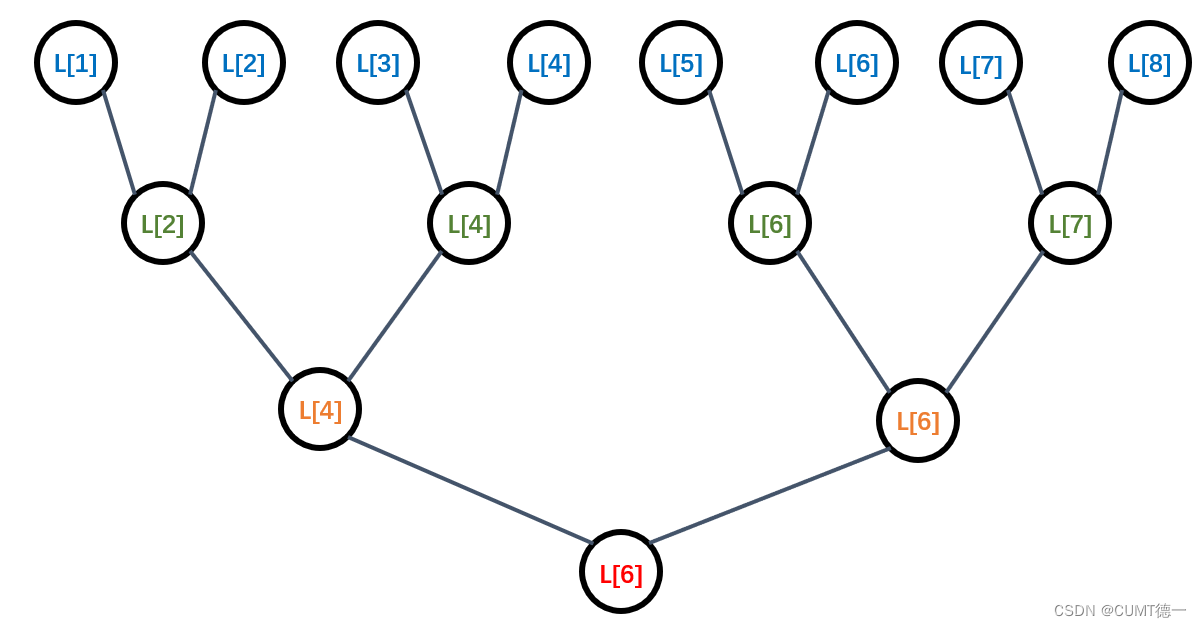
同样也做了n-1次比较，每一轮都有一半的元素被淘汰，如果n是一个以2为底的指数，那么就经过了 ${log_{2}}^{n}$ 轮比较，大体上，进行了⌈ ${log_{2}}^{n}$ ⌉轮比较，因此至多有 ⌈ ${log_{2}}^{n}$ ⌉个元素只丢失在了最大值上，可能是次大值，算法1可以被用来以 ⌈ ${log_{2}}^{n}$ ⌉-1次比较求出 ⌈ ${log_{2}}^{n}$ ⌉个元素序列的最大值，但算法2可以通过n+ ⌈ ${log_{2}}^{n}$ ⌉-2次比较寻找最大值和次大值（算法1需要n-1+n-2=2n-3步），因此算法得到了更大的提升。

我们还可以注意到，每一轮的所有比较，都可以并行的进行，因此，锦标赛方法为我们提供了一个并行计算的思路。

并行处理

我们在这里介绍一种并行计算模型PRAM

PRAM(Parallel Random Access Machine，随机存取并行机器)模型也称为共享存储的SIMD模型，是一种抽象的并行计算模型，在这种模型中，假定存在一台容量无限大的共享存储器，有有限台或无限台功能相同的处理器，且它们都具有简单的算术运算和逻辑判断功能，在任何时刻各处理器都可以通过共享存储单元相互交互数据。

几种处理写冲突的模式：

EREW: 单独(Exclusive)读，单独写。
ERCW：单独读，同时(Concurrent)写。
CREW：同时读，单独写。
CRCW：同时读，同时写。

我们为每个元素都提供一个处理器（Processor)，每一轮比较后，处理器数量减半。

斜线代表读操作，实心点代表处理器计算，虚线代表计算数值被保存到处理器的本地存储，双线代表写入数组。

如果一个读操作的线从 $P_{j}$ 到 $P_{i}$ （比如三条长斜线），那么代表着 $P_{i}$ 从数组M[j]中读取数据，也是 $P_{j}$ 写入的地方.

下图是一个并行算法，展示了所有处理器的工作过程:

下面给出该算法的伪代码：

A Parallel Tournament for Finding the Largest Key

Input: n个元素初始化在存储单元中：M[1],M[2],......M[n].
Output: 最大值会被存储在M[1]

注释：
每个处理器都有自己的序号i,每个处理器都有一个本地变量big,
它保存着目前为止读到的最大的元素值，
一个变量temp和一个变量incr，用于计算下一次读取的单元格号，
由于n可能不是2的幂，算法初始化单元格M[n+1],....M[2n]的值很小（负无穷）
，因为其中一些单元格会进入算法比较。

read M[i] into big;
incr:=1;
write -∞ {或一个非常小的值 } into M[n+i];
for step := 1 to ⌈log2n⌉ do
   read M[i+incr] into temp;
   big := max(big,temp);
   incr := 2*incr;
   write big into M[i] 
end { for }

算法分析：

进入for循环之前的初始化进行了一次“读/计算/写”步骤，for循环的每次迭代也进行一次“读/计算/写”步骤，总共加起来就是 ⌈ ${log_{2}}^{n}$ ⌉+1步，花费时间Θ( ${log_{2}}^{n}$ )。

此处有一个结论：

在t轮for循环结束后，每一个存储单元M[i]，1<=i<=n，都包含了 $x_{i}$ ,........, $x_{i+2^t-1}$ ，并且incr= $2^t$ 。

算法3：

如果我们允许多个处理器在同一时间向同一存储单元中写入数据（Common-Write)，那么可以得到一个比锦标赛方法花费时间更少的算法来求序列最大值。

该算法使用 $\frac{n(n-1)}{2}$ 个处理器，策略就是并行的比较所有的元素对，然后通过共享存储来交流结果，我们使用一个loser数组来占据存储单元M[n+1],...,M[2n].起初，数组中的所有元素值都为0，如果 $x_{i}$ 在一次比较中“lose"，那么loser[i]将会被赋值1。

算法如下：

Input：n个元素x1,x2,...,xn，初始化存储单元M[1],M[2],...M[n](n>2)
Output:最大值将会被存储在M[1]。

Step1:
     Pi,j reads xi (from M[i])

Step2:
     Pi,j reads xj (from M[j])
     Pi,j compares xi and xj
     Let k be the index of the smaller key.
     (如果元素相等，让k成为更小地址)
     Pi,j writes 1 in loser[k]
     {此时，除最大元素外的所有元素都输掉了一次比较}

Step3：
     Pi,i+1 reads loser[i](and P1,n reads loser[n]);
     任何处理器如果读到0都把xi写入到M[1].(P1,n would write xn)
     {Pi,i+1在它的本地存储中已经有了xi；P1,n也有xn}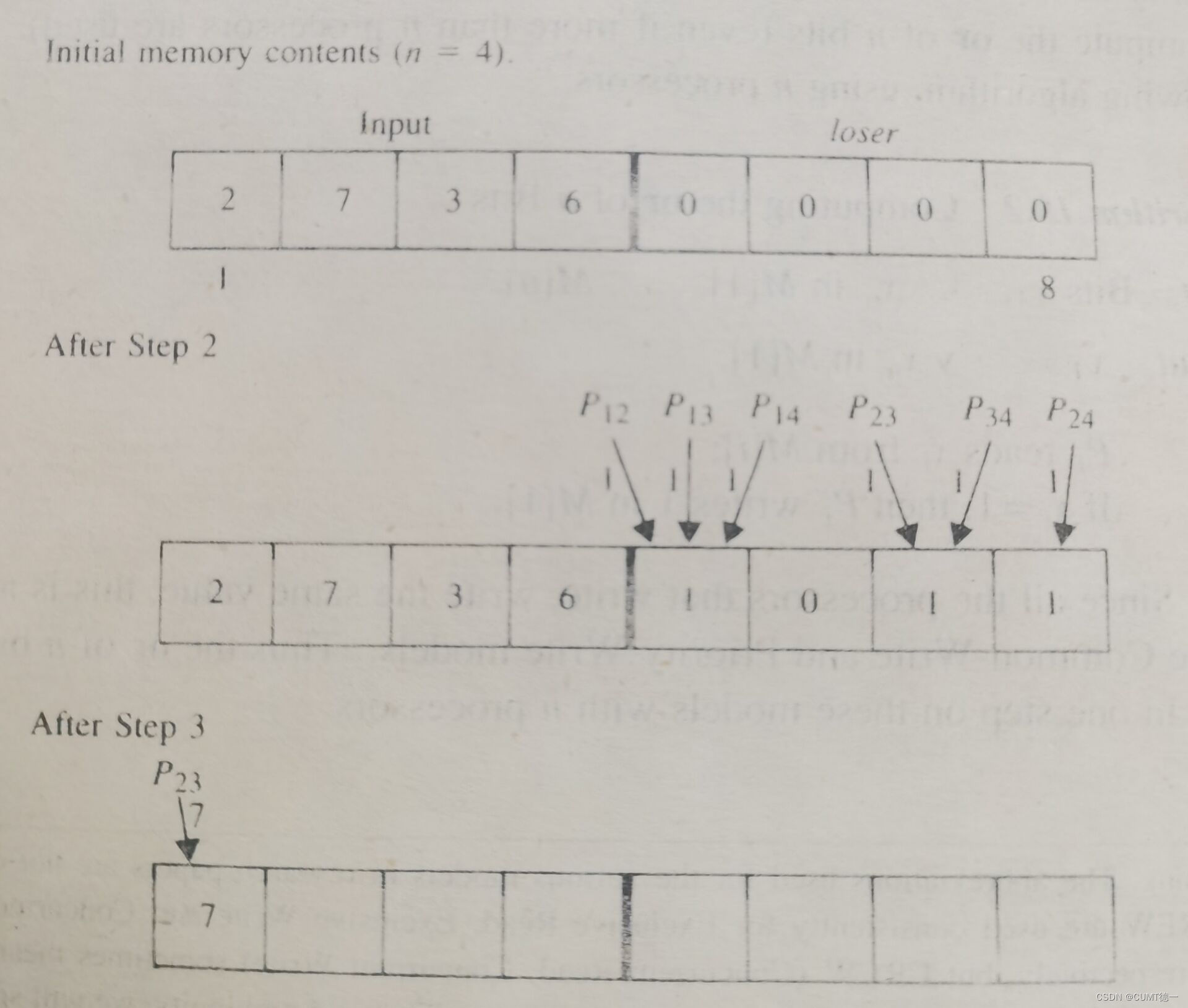

算法分析：

该算法使用的存储器数量为Θ( $n^2$ )，如果存储器数量限制在n，那么求最大元素值可以在O( $\log{_{2}}^{}log{_{2}}^{n}$ )内完成。

如果读者还想深入了解并行算法解决最大值查找问题，可以阅读文献[2],[3]。

二.并行归并排序

原始归并排序不在这里赘述，推荐读者阅读文章排序算法-归并排序_山风wind的博客-优快云博客_归并排序怎么算一趟

现在看并行归并排序：

归并排序的关键是如何实现两个有序序列的归并操作，原始归并排序算法通过使用辅助数组以及双指针的方式实现。

1.两个有序序列的合并操作

并行归并算法实现两个有序序列的合并操作如下：

（1）初始序列如图

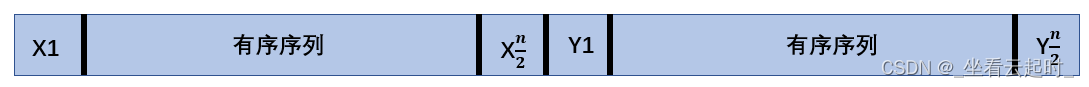
（2）二分搜索

处理器Pi取前一个有序序列中的值Xi，在后一个有序序列中做二分搜索，找到后一序列中比Xi大的最小的值Yj。（同理，后一序列中也可以在前一序列中进行二分搜索）

（3）移动该值到目标位置

根据（2）中操作可知前一序列中有i-1个值比Xi小，后一序列中有j-1个值比Xi小，那么归并之后，Xi应该位于整个有序序列的第（i-1+j-1+1=i+j-1）个位置，即M[i+j-1]。

（4）并行处理

因为这种操作并不移动各元素位置，所有的处理器都可以并行处理。

算法伪代码如下：

Input: 两个含有n/2个值的有序序列在存储器的前n个存储单元中，M[n]数组中
Output:一个归并后的有序序列，在存储器的前n个存储单元中

注释：每个处理器Pi都有一个本地变量x(如果i<=n/2),或者y(如果i>n/2)，和其他的用来进行二分搜索的本地变量，每个处理器都有一个本地可变地址会指明去哪里写它所存的元素。

初始化：
Pi把M[i]读入x(如果i<=n/2),或者y(如果i>n/2),为二分搜索做准备

二分搜索：
（1）处理器Pi(1<=i<=n/2),做二叉搜索在M[n/2+1],....,M[n]中寻找可以让X<M[n/2+j]的最小的j，并且把i+j-1作为目的地址(position)，如果找不到这个j，目的地址设为n/2+i
（2）处理器Pn/2+i(下标是n/2+i) (1<=i<=n/2),做二叉搜索在M[1],....,M[n/2]中寻找可以让Y<M[j]的最小的j，并且把i+j-1作为目的地址，如果找不到这个j，目的地址设为n/2+i

输出：
每个处理器(1<=i<=n)都把它所存的值(X或Y)写入到M[position]

算法分析：

由于二分搜索时间复杂度为O( $\log {_{2}}^{n}$ )，该并行算法在n/2个元素序列中做二分搜索，再加上处理器初始化的一步，总步骤为⌊ $\log{_{2}}^{\frac{n}{2}}$ ⌋+1，所以花费了O( $\log{_{2}}^{n}$ )。

2.归并排序总过程

Input:一个有n个值的列表，存储在M[1],...,M[n]中
Output：M[1],...,M[n]按升序排列

注释：如果元素值个数是2的幂会更简单，我们仍用n个处理器

处理器Pi把无穷大(一些很大的数)写入M[n+i]
for t:=1 to ⌈log2n⌉ do
   k := 2^(t-1);  {已经被归并操作后(两个有序序列合并)的列表大小
   Pi,...Pi+2k-1 合并两个排序过的列表(有序序列)
end { for }

算法分析与对比：

原始归并排序算法要归并 ⌈ ${log_{2}}^{n}$ ⌉趟（就是做 ⌈ ${log_{2}}^{n}$ ⌉遍合并两个有序序列操作），并行归并排序算法在该点与原始相同，也是 ⌈ ${log_{2}}^{n}$ ⌉趟，但是每一趟里面，原始归并的时间复杂度为O(n)，并行归并的时间复杂度为O( $\log{_{2}}^{n}$ )，由主定理法，原始归并总时间复杂度为O(n ${log_{2}}^{n}$ )，并行归并为O(n)，所以并行归并算法时间复杂度较小。

参考文献：

[1] Ames W F . Computer Algorithms — Introduction to design and analysis (second edition)[J]. Mathematics and Computers in Simulation, 1990, 31(6):602-602.

[2]贺成,施华君.基于PRAM并行模型最大值查找的方法与改进[J].计算机系统应用,2019,28(10):138-144.DOI:10.15888/j.cnki.csa.007119.

[3]Shiloach Yossi,Vishkin Uzi. Finding the maximum, merging, and sorting in a parallel computation model[J]. Journal of Algorithms,1981,2(1).

[4]排序算法-归并排序_山风wind的博客-优快云博客_归并排序怎么算一趟