数模打卡--图的最短路径及距离

图的最短路径和距离

准备

1.创建稀疏矩阵

1.1什么是稀疏矩阵

在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵；与之相反，若非0元素数目占大多数时，则称该矩阵为稠密矩阵。

矩阵稠密度：非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度。

1.2 sparse函数

S = sparse(A)

将矩阵A转化为稀疏矩阵形式，即矩阵A中任何0元素被去除，非零元素及其下标组成矩阵S。如果A本身是稀疏的，sparse(S)返回S。

例子

有以下矩阵：A=[1,0,2;2,0,0;3,1,0]

S=sparse(A)

运行结果：

此时已经剔除全部0元素。

2.有向图的最短路径

下面是一个带权重的无向图：
matlab代码：

%w(a,b)=权重
w=zeros(4);
w(1,2)=2;
w(2,1)=2;
w(1,3)=1;
w(3,1)=1;
w(2,4)=3;
w(4,2)=3;
w(3,4)=4;
w(4,3)=4;
s=sparse(w);

运行结果：

还可以用另外一种方法创建稀疏矩阵
G=sparse([起点集合],[对应终点集合],[权重值])

G=sparse([1,2,1,3,2,4,3,4],[2,1,3,1,4,2,4,3],[2,2,1,1,3,3,4,4]);
s=sparse(G);

运行结果一样。由此我们可以进行下一步使用函数graphallshortestpaths来求取有向图的最短路径。

2.1.geaphallshortestpaths函数

%创建一个包含4个节点8条边的有向图
W = [2 2 1 1 3 3 4 4];
DG = sparse([1 2 1 3 2 4 3 4],[2 1 3 1 4 2 4 3],W);

画出有向图：

h = view(biograph(DG,[],'ShowWeights','on'));

查找最短路径：

graphallshortestpaths(DG);

主对角线上的元素全为0，是因为所有节点都没有自回路。根据结果我们可以知道从节点一道节点四的最短距离为5。其余节点之间的距离依次可以根据结果知道。

2.2.dijkstra函数

function [min,path]=dijkstra(w,start,terminal)
n=size(w,1); label(start)=0; f(start)=start;
for i=1:n
   if i~=start
       label(i)=inf;
end, end
s(1)=start; u=start;
while length(s)<n
   for i=1:n
      ins=0;
      for j=1:length(s)
         if i==s(j)
            ins=1;
         end
      end
      if ins==0
         v=i;
         if label(v)>(label(u)+w(u,v))
            label(v)=(label(u)+w(u,v)); 
         f(v)=u;
         end 
      end
   end   
v1=0;
   k=inf;
   for i=1:n
         ins=0;
         for j=1:length(s)
            if i==s(j)
               ins=1;
            end
         end
         if ins==0
            v=i;
            if k>label(v)
               k=label(v);  v1=v;
            end
         end
   end
   s(length(s)+1)=v1;  
   u=v1;
end
min=label(terminal); path(1)=terminal;
i=1; 
while path(i)~=start
      path(i+1)=f(path(i));
      i=i+1 ;
end
path(i)=start;
L=length(path);
path=path(L:-1:1);

直接调用这个函数也可以求得最短路径。

DG=zeros(4);
W = [2 2 1 1 3 3 4 4];
DG = sparse([1 2 1 3 2 4 3 4],[2 1 3 1 4 2 4 3],W);
DG(DG==0)=inf;
DG(eye(4,4)==1)=0;
h = view(biograph(DG,[],'ShowWeights','on'));%画出有向图
[min,path]=dijkstra(DG,1,4);

运行结果：

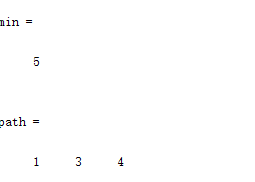
3.无向图的最短路径

3.1.shortestpath函数

DG=zeros(4);
W = [2 2 1 1 3 3 4 4];
DG = graph([1 2 1 3 2 4 3 4],[2 1 3 1 4 2 4 3],W);
plot(DG,'EdgeLabel',DG.Edges.Weight)
[path min]=shortestpath(DG,1,4)

运行结果：

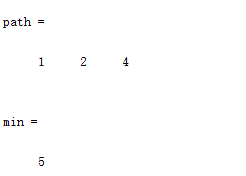
path= 1 2 4(路径)
min=5（最短距离）。

3.2.使用graphallshortestpaths函数

W = [2 2 1 1 3 3 4 4];
G = sparse([1 2 1 3 2 4 3 4],[2 1 3 1 4 2 4 3],W);
view(biograph(G,[],'ShowArrows','off','ShowWeights','on'))
graphallshortestpaths(G,'directed',false)%false代表无向图true代表有向图

运算结果：
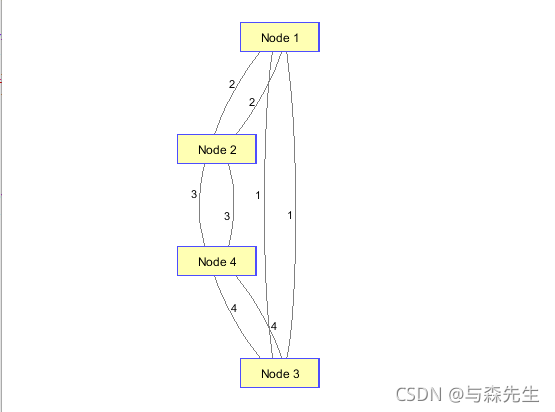
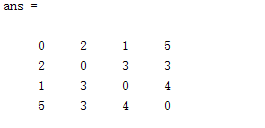节点一到节点四的最短距离为5