2021牛客寒假算法基础训练营补题

2021牛客寒假算法基础训练营1补题 - H

题目描述

输入描述

第一行输入一个正整数a。
第二行输入一个正整数n。
(1 <= a, n <= 10^100000)

输出描述

一个数字，代表幂塔的个位数

样例

输入

3
3

输出

7

说明

3³^³ = 3^27 = 7625597484987，个位数是7

解析

不要被实例骗到了，那么大的数，不可能先求出来再取个位数，所以必须要找规律。

规律

以0，1，5，6结尾的数的规律是最容易找的，因为无论多少个这种数相乘，得到的数的个位都为它本身。别的数规律也能慢慢找到。

例子

9结尾的数，1个9相乘个位为9，2个相乘个位为1，即奇数个的9相乘，个位为9，偶数个的9相乘，个位为1，又因为幂塔是a^a，所以必定是奇数个的9相乘，个位数为9，规律就找到了。
2结尾的数比较难推，我在这里说明一下，和9一样，先看1个2相乘为2，2个2相乘为4……可以发现，每4个2相乘，个位数就是一个循环，分别为2 4 8 6，所以只需要知道指数%4余数为几，就可以知道个位数是多少了，但是2有一个非常神奇的地方（8也是这个规律），我们假设以2结尾的数是a，a^a % 4结果必为0，证明如下：

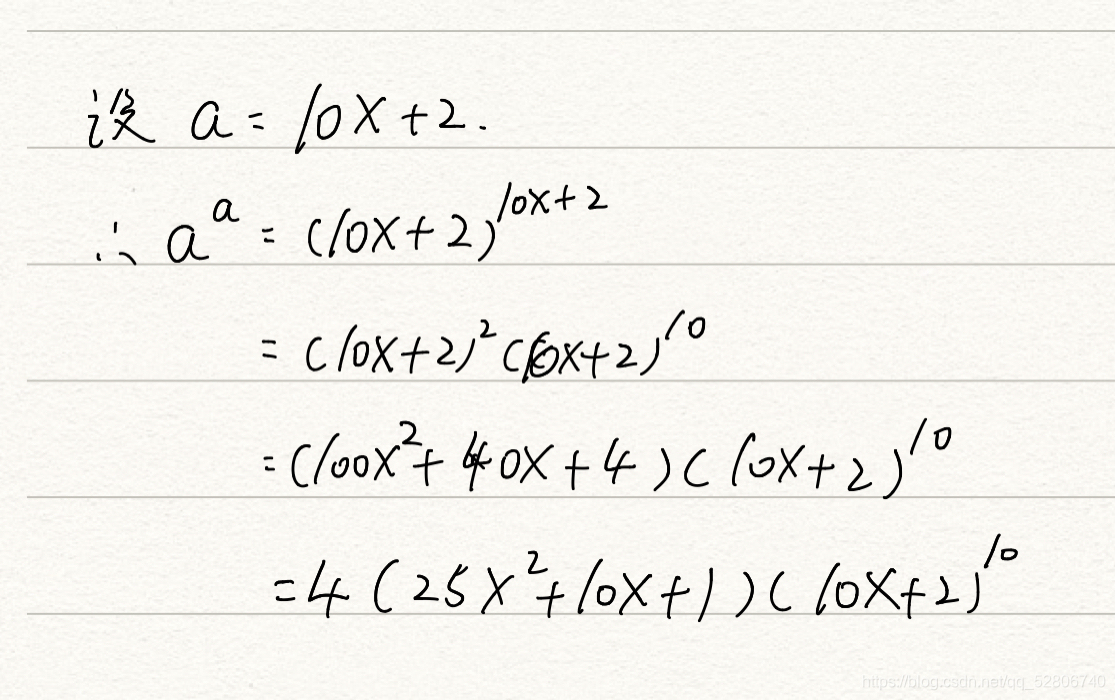
其余的数找规律只需要看这个数的最后两位%4的结果即可，至于为啥自己可以推一下。

注意

这道题目a, n的输入范围非常大，所以必须要用字符串的形式读入，不难搞错了，代码方面还是比较简单的，规律找到了就容易了。

代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int K = 1e9;
const int N = 100010;

char s1[N], s2[N];

int main()
{
	cin >> s1 >> s2;
	int l1 = strlen(s1);
	int l2 = strlen(s2);
	if (l2 == 1 && s2[0] == '1')
	{
		cout << s1[l1 - 1];
	}
	else
	{
		int x = s1[l1 - 1] - '0';//个位数
		int y = ((s1[l1 - 2] - '0') * 10 + s1[l1 - 1] - '0') % 4;//最后两位数 % 4的结果
		switch (x)
		{
		case(0):
		case(1):
		case(5):
		case(6):
		case(9):
			cout << x;
			break;
		case(2):
		case(8):
			if (l2 == 1 && s2[0] == '2' && y != 0)
				cout << 4;
			else
				cout << 6;
			break;
		case(3):
			if (y == 1)
				cout << 3;
			else
				cout << 7;
			break;
		case(4):
			cout << 6;
			break;
		case(7):
			if (y == 3)
				cout << 3;
			else
				cout << 7;
			break;
		}
	}
	return 0;
}