腐烂的橘子（leetcode994）

题目

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

• 值 0 代表空单元格；
• 值 1 代表新鲜橘子；
• 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

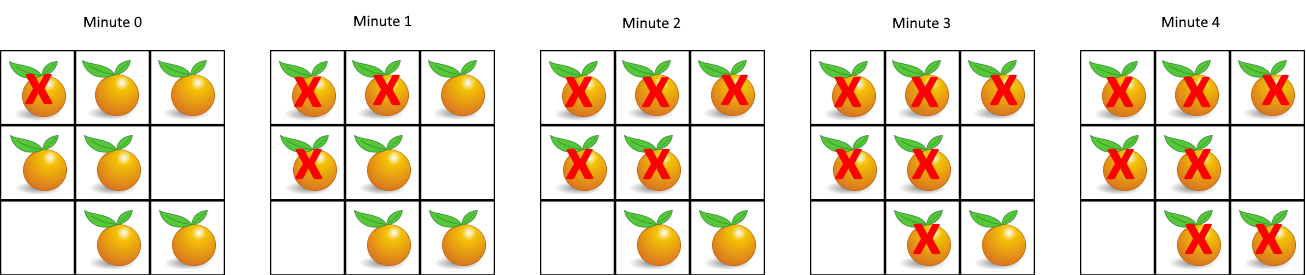
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

思路

多源广度优先遍历，与一般遍历相比，就只需要先遍历整个图找到多个腐烂的橘子（起点），然后加入队列即可。在腐烂时间问题的处理上：

第一次：（感觉不太好有点绕）

在求腐烂的时间问题上需要注意，若移动到某格，四个方向都不可移动，仍然会造成时间加一，找了好久发现这个地方，可以通过一个flag变量，来标记是否能够移动，能移动的话flag标记为1，四个方向都不能的话标记0，只有在flag为1的情况下，腐烂时间再进行+1。

例如 [ [0,2] ]；此时只有一个坏橘子，从坏橘子坐标开始遍历，发现四个方向都不可移动，但是变坏时间却会+1。

第二次：

加了time数据来存储每个坐标的腐烂时间，这样就避免了一些特殊情况的考虑

代码

第一种

class Solution {
public:
    typedef pair<int, int> PII;
    int dx[4] = {0, 1, -1, 0}, dy[4] = {1, 0, 0, -1};
    int ans = 0;
    int cnt = 0;
    int flag = 0;//用来标记四个方向是否能移动
    queue<PII> q;
    bool check(int x, int y, int n, int m) {
        return x >= 0 && y >= 0 && x < n && y < m;
    }
    int orangesRotting(vector<vector<int>>& grid) {
        int n = grid.size();
        int m = grid[0].size();
        for(int i = 0;i < n;i++)
            for(int j = 0;j < m;j++)
            {
                if(grid[i][j] == 2)
                    q.push({i,j});
                if(grid[i][j] == 1)
                    cnt++;
            }

        while(!q.empty())
        {
            int size = q.size();
            flag = 0;
            while(size--)
            {
                auto temp = q.front();
                q.pop();
                for(int i = 0;i < 4;i++)
                {
                    int x = temp.first + dx[i];
                    int y = temp.second + dy[i];
                    if(check(x,y,n,m) && grid[x][y] == 1)
                    {
                        grid[x][y] = 2;
                        cnt--;
                        flag = 1;
                        if(!cnt)
                            break;
                        q.push({x,y});
                    }
                }
            }
            if(flag)
                ans++;
        }
        return cnt ? -1 : ans;
    }   
};

第二种

class Solution {
public:
    typedef pair<int, int> PII;
    int dx[4] = {0, 1, -1, 0}, dy[4] = {1, 0, 0, -1};
    int ans = 0;
    int cnt = 0;
    int flag = 0;
    int time[11][11];
    queue<PII> q;
    bool check(int x, int y, int n, int m) {
        return x >= 0 && y >= 0 && x < n && y < m;
    }
    int orangesRotting(vector<vector<int>>& grid) {
        int n = grid.size();
        int m = grid[0].size();
        for(int i = 0;i < n;i++)
            for(int j = 0;j < m;j++)
            {
                if(grid[i][j] == 2)
                    q.push({i,j});
                if(grid[i][j] == 1)
                    cnt++;
            }

        while(!q.empty())
        {
            auto temp = q.front();
            q.pop();
            for(int i = 0;i < 4;i++)
            {
                int x = temp.first + dx[i];
                int y = temp.second + dy[i];
                if(check(x,y,n,m) && grid[x][y] == 1)
                {
                    //每次加入新坐标进队列就更新time时间
                    time[x][y] = time[temp.first][temp.second] + 1;
                    grid[x][y] = 2;
                    cnt--;
                    ans = time[x][y];
                    q.push({x,y});
                    if(!cnt) break;
                }
            }
        }
        return cnt ? -1 : ans;
    }   
};