文章讲述了平面图形在直角坐标系和极坐标系下的面积计算，包括弧长、旋转体体积的求解，以及函数平均值的计算。使用了微积分中的积分法，特别提到了换元法在解决复杂问题时的应用。同时涵盖了曲线绕轴旋转产生的体积问题。
第九讲 一元微分学的几何应用
重点
- 平面图形面积——极坐标系下的换元法
- 旋转体体积
- 函数平均值
- 弧长的计算问题
平面图形的面积
直角坐标系下
直接算
曲线包围
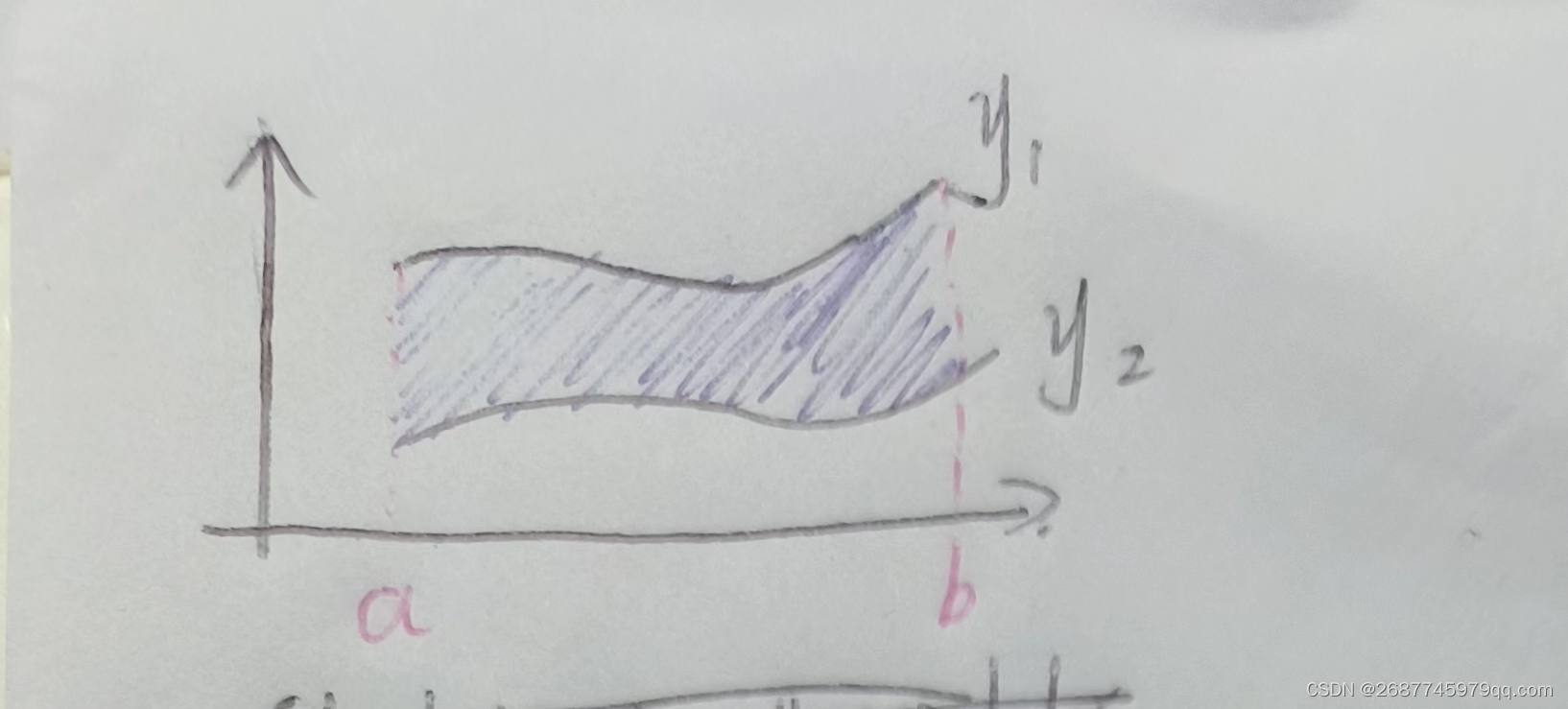
S
=
∫
a
b
∣
y
1
−
y
2
∣
d
x
S=\int_{a}^{b}\left|y_{1}-y_{2}\right| \mathrm{d} x
S=∫ab∣y1−y2∣dx
弧形面积
S
=
1
2
∫
a
β
∣
r
1
2
(
θ
)
−
r
2
2
(
θ
)
∣
d
θ
S=\frac{1}{2} \int_{a}^{\beta}\left|r_{1}^{2}(\theta)-r_{2}^{2}(\theta)\right| \mathrm{d} \theta
S=21∫aβ
r12(θ)−r22(θ)
dθ
所谓的底乘高
底是
r
(
θ
)
d
θ
r(\theta )d\theta
r(θ)dθ
高是
r
(
θ
)
r(\theta )
r(θ)
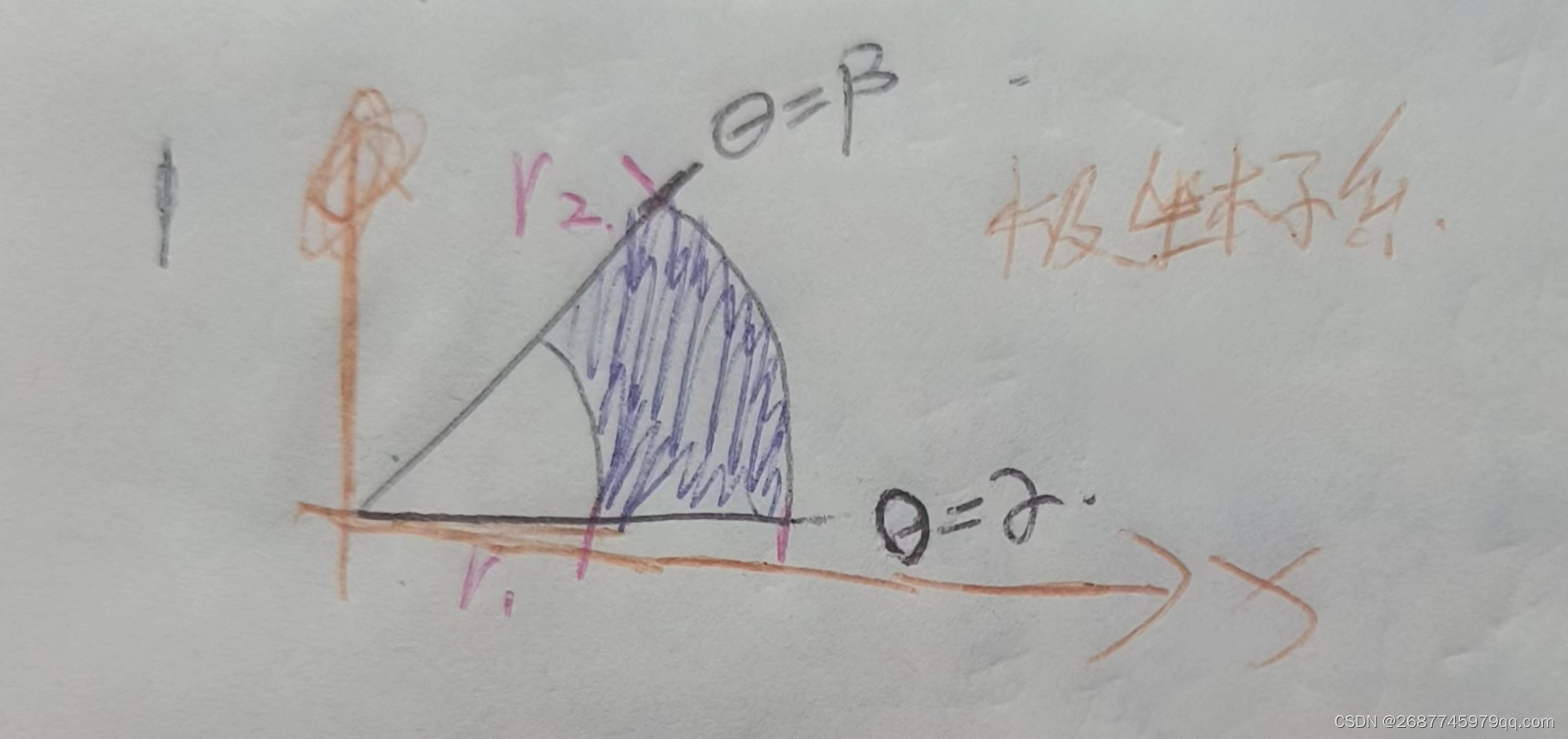
参数方程下
少数直接算
换元法
众所周知，换元要三换
- 上下限
- 被积函数
- d x dx dx
{ x = x ( t ) y = y ( t ) \left\{\begin{array}{l}x=x(t) \\y=y(t)\end{array}\right. {x=x(t)y=y(t)
旋转体体积
一条曲线绕 x x x
V = π ∫ a b y 2 d x V=\pi \int_{a}^{b}y^{2} \mathrm{d} x V=π∫aby2dx
两条曲线绕 x x x
V = π ∫ a b ∣ y 1 2 − y 2 2 ∣ d x V=\pi \int_{a}^{b}\left|y_{1}^{2}-y_{2}^{2}\right| \mathrm{d} x V=π∫ab y12−y22 dx
一条曲线绕 y y y
V y = 2 π ∫ a b x ∣ y ∣ d x V_{y}=2 \pi \int_{a}^{b} x|y| \mathrm{d} x Vy=2π∫abx∣y∣dx
两条曲线绕 y y y
V y = 2 π ∫ a b x ∣ y 1 − y 2 ∣ d x V_{y}=2 \pi \int_{a}^{b} x|y_{1}-y_{2}| \mathrm{d} x Vy=2π∫abx∣y1−y2∣dx
计算函数平均值
设 x ∈ [ a , b ] , 函数 y ( x ) 在 [ a , b ] 上的平均值为 \text { 设 } x \in[a, b] \text {, 函数 } y(x) \text { 在 }[a, b] \text { 上的平均值为 } 设 x∈[a,b], 函数 y(x) 在 [a,b] 上的平均值为
y ˉ = 1 b − a ∫ a b y d x \bar{y}=\frac{1}{b-a} \int_{a}^{b} y \mathrm{d} x yˉ=b−a1∫abydx
等价于积分中值定理
扫一扫
1390
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
