如何在未知iv值情况下如何进行手工破译ROT密文?

事件

在阅读到关于密码学加解密的时候,突然间想到是否在未知iv值的情况下手工破译ROT密文。
于是觉得利用频率分析来破解也许可行，以下是我的思路。

示例 “FRQJUDWXODWLRQVBRXJRWLW”

1.绘制索引表格

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26
A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z

2.频率分析

在英文中 E,T,A,O,N,R,I,S,H 这些字母使用频率是最高的

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26
A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z

1.统计字符串中出现的最高次数频率的字符
"FRQJUDWXODWLRQVBRXJRWLW"

字母	出现次数
B	1
D	2
F	1
J	2
L	2
O	1
Q	2
R	4
U	1
V	1
W	4
X	2

3.假定向量iv

定义一个iv向量,X为加密字符串中出现的最高次数频率的字符的索引

$$\mathbf{iv}=\left[\begin{array}{c}X-5\\ X-20\\ X-1\\ X-15\\ X-14\\ X-18\\ X-9\\ X-19\\ X-18\end{array}\right]$$

本次示例中R的索引(18)作为X
带入计算得
iv=[13,−2,17,3,4,0,9,−1,0]

4.连贯性猜解

密文:"FRQJUDWXODWLRQVBRXJRWLW"

F	R	Q	J	U	D	W	X	O	D	W	L	R	Q	V	B	X	J	R	W	L	W
6	18	17	10	21	4	23	24	15	4	23	12	18	17	22	2	24	10	18	23	12	23

将密文索引逐一带入Pi，并且每一个索引值都要减去假定iv值

$$S_{i,j}=(((P_i-i{v}_j)\mathrm{mod}26)+26)\mathrm{mod}26$$

---

先获取前三个字母

P_i (F=6)	6	6	6	6	6	6	6	6	6
iv_j	13	-2	17	3	4	0	9	-1	0
S_{0,j}	19	8	15	3	2	6	23	7	6
对应字母	S	H	O	C	B	F	W	G	F

---

P_i (R=18)	18	18	18	18	18	18	18	18	18
iv_j	13	-2	17	3	4	0	9	-1	0
S_{1,j}	5	20	1	15	14	18	9	19	18
对应字母	E	T	B	O	N	S	I	T	S

---

P_i (Q=17)	17	17	17	17	17	17	17	17	17
iv_j	13	-2	17	3	4	0	9	-1	0
S_{2,j}	4	19	0	14	13	17	8	18	17
对应字母	D	S	A	N	M	R	I	S	R

---

根据相同的 iv_j 进行整理，我们按照 iv_j 的顺序 逐列组合 得到最终字符串(寻找具有单词连贯性的字符)：

iv_j	第 1 行 (F=6)	第 2 行 (R=18)	第 3 行 (Q=17)
13	S	E	D
-2	H	T	S
17	O	B	A
3	C	O	N
4	B	N	M
0	F	S	R
9	W	I	I
-1	G	T	S
0	F	S	R

---

5.解密

仅仅取iv_j=3继续依次计算解密

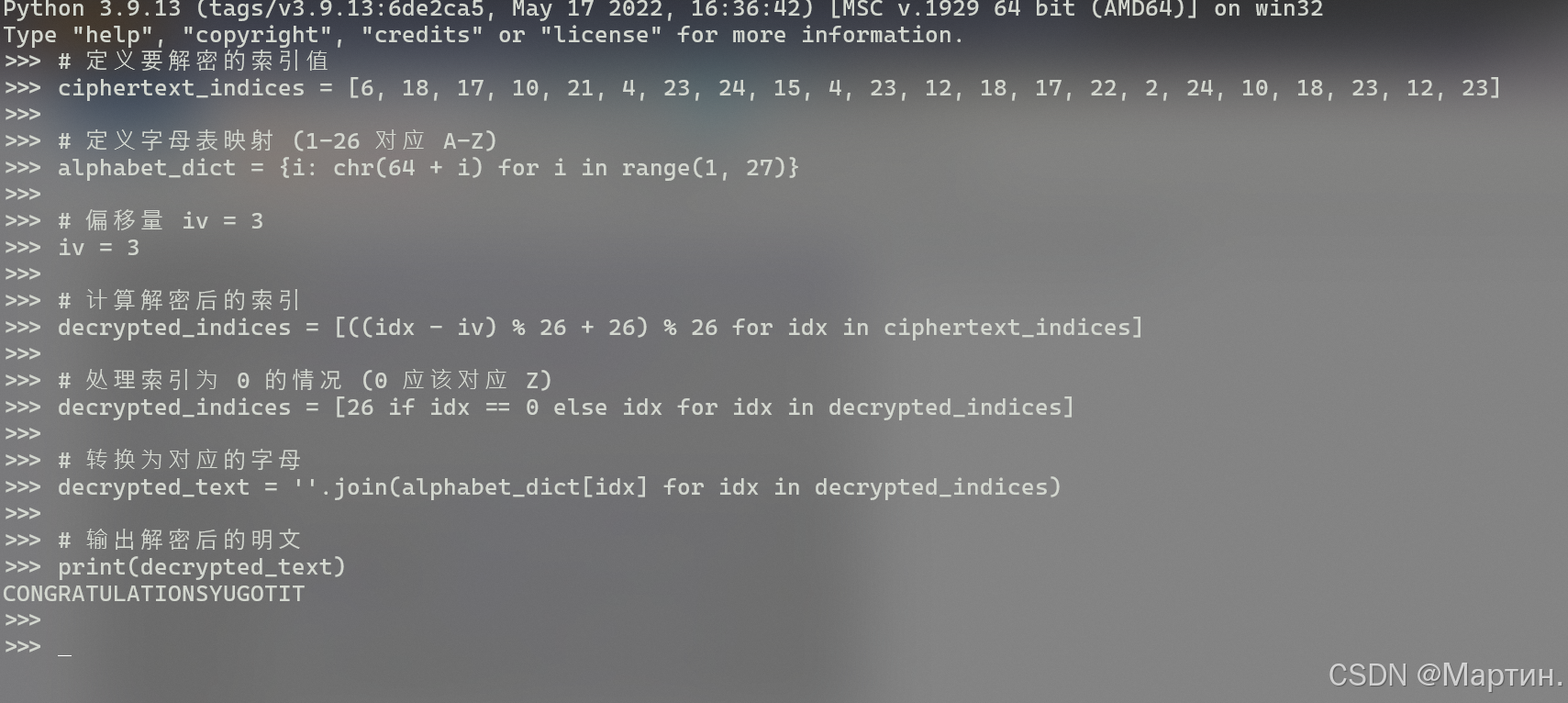
明文:CONGRATULATIONSYUGOTIT

"CONGRATULATIONS YOU GOT IT"

最终iv=3