机器学习与深度学习关键概念解析：数据集划分、优化算法与神经网络结构-优快云博客

本文概述了机器学习中的关键概念，包括训练、测试和验证数据集的区别，权重衰退现象，PyTorch中的基础操作，如梯度清除，以及深度学习中的卷积层、学习率、批量大小、池化层和全连接层的作用。重点讲解了LeNet和VGG网络结构。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

都是一些细碎的小小点，希望能给自己和大家带来一点启发

第八节线性回归 + 基础优化算法

第九节 softmax

第十一节模型选择 + 过拟合和欠拟合

一）机器学习的训练数据集，测试数据集和验证数据集分别是什么，有什么区别

一）强化学习中的学习率（learning rate）和批量大小（batch size）与学习曲线的抖动关系

一）卷积神经网络中，池化操作与维度数量的关系是怎么计算的

二）对于卷积神经网络的进一步理解

三）最后全连接层的作用

一、

在默认情况下，PyTorch会累积梯度，因此在进行另外一个函数之前需要清除之前的值

x.grad.zero_()

y = x.sum()

y.backward()

x.grad

PyTorch中下划线表示重写内容，zero_表示把所有的梯度清零

第八节线性回归 + 基础优化算法

第九节 softmax

这里的log应该都是以e为底数

第十一节模型选择 + 过拟合和欠拟合

一）机器学习的训练数据集，测试数据集和验证数据集分别是什么，有什么区别

在机器学习中，通常将数据集划分为三个主要部分：训练数据集（Training Dataset）、测试数据集（Test Dataset）、和验证数据集（Validation Dataset）。这三个数据集的目的和用途如下：

1、训练数据集（Training Dataset）：

训练数据集是用于训练机器学习模型的数据子集。
它包含了大部分或全部的标记（ground truth）数据，即特征和相应的正确标签或输出。
模型通过学习训练数据集来调整参数和权重，以适应数据的模式和关系。
训练数据集用于训练模型的过程，通过反复迭代和调整参数来减小模型的预测误差。

2、测试数据集（Test Dataset）：

测试数据集是用于评估训练后模型性能的数据子集。
它包含了特征数据，但不包含标签或输出，模型的目标是根据学到的模式进行预测。
测试数据集用于衡量模型在未见过的数据上的泛化能力，即模型对新数据的预测性能如何。
通过测试数据集，可以估计模型的性能，如准确度、精确度、召回率等。

3、验证数据集（Validation Dataset）：

验证数据集是用于调整模型超参数（如学习率、正则化参数等）的数据子集。
它类似于测试数据集，包含特征数据和对应的标签，但通常不同于训练和测试数据集。
验证数据集用于评估不同超参数设置下模型的性能，并帮助选择最佳的超参数配置。
这有助于防止模型对测试数据过度拟合，因为模型在训练过程中未看到验证数据。

区别总结：

训练数据集用于训练模型的参数，测试数据集用于评估模型的性能，而验证数据集用于调整模型的超参数。
训练数据集包含标签，测试数据集通常不包含标签，验证数据集也包含标签。
训练数据集是用来建立模型的，测试数据集是用来评估模型的泛化能力，验证数据集是用来选择超参数的。

二）测试数据集只能用一次吗

在标准的机器学习实验中，测试数据集通常只应该用一次来评估模型的性能。这是因为测试数据集的目的是模拟模型在未见过的新数据上的性能表现，用于衡量模型的泛化能力。

如果在训练过程中多次使用测试数据集来调整模型或超参数，那么模型可能会对测试数据过拟合，也就是说它会适应特定的测试数据，但在真实世界中的新数据上表现很差。这会导致对模型性能的不准确估计，因为模型已经过多次测试数据集的反复训练和调整。

因此，为了准确评估模型的泛化性能，测试数据集通常只在模型训练完毕之后使用一次。如果需要调整模型的超参数，通常会使用验证数据集，以确保测试数据集保持不受干扰，用于最终的性能评估。这种分离测试数据集和验证数据集的做法有助于更好地估计模型在真实环境中的性能。

第十二节权重衰退

为什么一个只包含20个样本的小训练集更容易过拟合

有限的样本多样性：小训练集中的样本数量有限，可能无法充分代表整个数据分布。这导致模型可能会过于依赖于这些有限的样本，而忽略了更广泛数据集的变化和多样性。过拟合就是模型在训练数据上表现得很好，但在未见过的数据上表现不佳的现象，这是因为模型过于适应了训练数据中的噪声和随机性。
噪声的影响：小训练集中的个别噪声点或异常值可能会对模型产生不适当的影响。模型可能会试图拟合这些噪声，而不是真正的数据模式。
参数数量较多：如果您的模型具有大量的参数，相对于小训练集的大小，模型将有更多的自由度来调整参数以适应训练数据。这使得模型更容易过拟合，因为它可以过度灵活地拟合训练数据中的噪声。
正则化的需求：小训练集更容易受到过拟合的影响，因此通常需要更强的正则化来限制模型的复杂度。正则化技术，如L1和L2正则化，可以帮助降低模型的复杂度，减少过拟合的风险。

第十六节 PyTorch 神经网络基础

一）关于就地操作

二）关于m.weight.data *= m.weight.data.abs() >= 5，即布尔掩码

第十九节卷积层

一）强化学习中的学习率（learning rate）和批量大小（batch size）与学习曲线的抖动关系

1、学习率（Learning Rate）：

学习率决定了每次参数更新的步长。较高的学习率会导致参数更新幅度较大，从而在训练过程中可能出现剧烈的参数波动。这种情况下，模型可能会难以稳定地收敛，甚至会发散。
较低的学习率可以使参数更新更加稳定，但需要更多的训练时间，因为每次更新的步长较小。这可以减小曲线的抖动，但可能需要更多的训练迭代才能获得良好的性能。
选择适当的学习率通常需要通过实验来确定，可以尝试不同的学习率值，观察模型的收敛情况以及性能。

2、批量大小（Batch Size）：

较大的批量大小可以带来更稳定的梯度估计，因为它们基于更多的样本数据。这通常会减小训练中的参数更新的方差，使训练过程更加平滑。
较小的批量大小可能会导致更大的参数更新方差，因为它们基于较少的样本数据，这可能会导致训练曲线的抖动。
批量大小的选择也需要根据具体问题和计算资源进行权衡。较大的批量大小可能需要更多的内存和计算资源。

第二十节卷积层里的填充和步幅

一）执行卷积前要增加一个一个批量大小和一个通道数的维度

在深度学习中，卷积神经网络（Convolutional Neural Networks，CNNs）通常是设计用于处理多个输入示例（批量数据）和多个通道（特征映射）的情况。这是因为卷积操作具有很好的参数共享性质，可以同时处理多个示例和多个特征映射，以提取图像或其他数据的特征。

批量大小（Batch Size）：深度学习中通常使用小批量（mini-batch）训练来加速模型训练过程。每个小批量包含多个输入示例，这有助于提高模型的泛化性能和收敛速度。因此，通常会将多个输入示例组成一个批量，这就是为什么要增加批量大小的维度。在卷积操作中，批量大小指示着你要同时处理多少个输入示例，每个示例都会通过相同的卷积核进行卷积操作，从而加速训练过程。
通道数（Channel/Feature Maps）：卷积神经网络通常包含多个卷积核（也称为滤波器），每个卷积核用于捕捉不同的特征。通道数指的是卷积核的数量，每个通道对输入数据执行卷积操作并生成一个特征映射。这些特征映射可以看作是对输入数据不同特征的提取。因此，在卷积操作中，需要指定要使用多少个卷积核（通道数）来提取不同的特征信息。

李沐老师的视频里面，都是只有一个卷积核和一个batch，所以添加的两个通道都是1

第二十二节池化层

一）padding参数相关

这里我一开始有点混乱

conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)

这里padding=1，也就是在外面“围一圈”

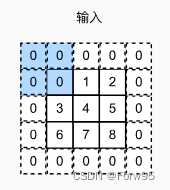也就是外面这一圈的0

pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))

这里padding=(0, 1)，也就是高度上增加零行，宽度上增加一行，也就是列数增加了

第二十三节经典卷积神经网络 LeNet

一）卷积神经网络中，池化操作与维度数量的关系是怎么计算的

在卷积神经网络（CNN）中，池化操作（如最大池化或平均池化）是用于减少特征图（feature map）维度的一种方法。这个操作有助于降低计算复杂度，并且能提取出更抽象级别的特征。池化操作通常会减少数据的空间大小，但保持深度（即通道数）不变。计算池化后的维度，需要考虑以下几个因素：

输入维度：输入特征图的宽度（W）、高度（H）和深度（D）（李沐的课一般讲宽度和高度）。
池化尺寸：池化操作的窗口大小，通常表示为宽度（F_W）和高度（F_H）。例如，2x2 或 3x3。
步长（Stride）：窗口移动的步长，通常表示为 S。这决定了池化窗口在特征图上的移动距离。
填充（Padding）：有时在输入特征图的边缘添加额外的零填充。在池化操作中，这种情况不太常见，但如果存在，则需要考虑（现在pooling也不常见了）。

计算池化后的维度时，通常使用以下公式：

输出宽度：(W - F_W) / S + 1
输出高度：(H - F_H) / S + 1
输出深度：D

请注意，输出深度保持不变，因为池化操作通常只影响宽度和高度。如果使用了填充，公式会稍有不同，需要将填充量考虑在内。

举个例子两个例子，

①举个例子，假设我们有一个 8x8的特征图（宽度8，高度8），使用2x2的池化窗口和步长为2，没有填充。

nn.AvgPool2d(kernel_size=2, stride=2)

那么池化后的输出维度将是：

输出宽度：(8 - 2) / 2 + 1 = 4
输出高度：(8 - 2) / 2 + 1 = 4
输出深度：3

因此，输出的维度将是 4x4。

这也是LeNet中图片28*28的维度变成14*14的原因

②假设我们有一个 8x8x3 的特征图（宽度8，高度8，深度3），使用2x2的池化窗口和步长为2，没有填充。那么池化后的输出维度将是：

输出宽度：(8 - 2) / 2 + 1 = 4
输出高度：(8 - 2) / 2 + 1 = 4
输出深度：3

因此，输出的维度将是 4x4x3。

二）对于卷积神经网络的进一步理解

整个思想就是对于初始的输入——>不断增加通道（卷积操作）与降低每一个通道的维度（pooling操作），这样子做的目的是分离出这个信息（图片等）的不同信息。直观地说，我们可以将每个通道看作对不同特征的响应。先把他分散开来——>展平，使用全连接层进行聚合，输出分类。

三）最后全连接层的作用

特征整合：在经过几层卷积和池化操作后，网络会产生多个高级别的特征图。全连接层的主要作用是将这些特征图整合成一个一维特征向量，这有助于对特征进行更加全面的分析和处理。也就是将局部信息转换为整体信息。
决策制定：卷积层和池化层主要负责从输入图像中提取特征。而全连接层则用于基于这些特征做出决策（如分类）。它们通过权重将这些特征转换为最终的输出，如分类标签。
网络深度和复杂度：在LeNet时代，计算资源相对有限。使用全连接层是一种有效的方式来构建较深的网络结构，同时保持计算和参数的可管理性。

最后随意补一个小知识点，隐藏层的节点数不能太大，这样子会导致overfitting，即网络的泛化性不好。这是由于网络的自由度更高了，这会让它去学习一些噪声的过多的细节，这样子就没有好的泛化性能了。

第二十五节使用块的网络 VGG

记录一个解包操作

return nn.Sequential(*layers)

layers 是一个包含一系列层的列表，其中每个层要么是卷积层 (nn.Conv2d)，要么是 ReLU 激活 (nn.ReLU)，要么是最大池化层 (nn.MaxPool2d)。
nn.Sequential(*layers) 创建了一个用于这些层的顺序容器。*layers 语法用于解包 layers 列表的元素，并将它们作为单独的参数传递给 nn.Sequential。这是一种简洁的方式，用于将列表中的所有层作为参数传递给 Sequential 构造函数。

因此，return nn.Sequential(*layers) 等同于使用指定的层创建一个 nn.Sequential 容器，这使得以顺序方式定义和组织神经网络的层变得更加简便。

源代码：

import torch
from torch import nn
from d2l import torch as d2l


def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels,
                                kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)