2021 MIT || 麻省理工机器学习导论(一)
YOUTube:MIT 6.S191: Introduction to Deep Learning(要梯子,可以去B站上找找,好像也有)
这些是我在学习一点机器学习后,回过头来重新学习相关的基础,内容主要包含了上课的笔记,以及一些见解。关于各个模块更详细的内容请另寻它处,这篇笔记主要是对机器学习框架的构建。
The Perceptron:Forward Propagation
单层感知机
先以一个神经元为例子(单个神经元为单层感知机,多个神经元为多层感知机)

- X i ∈ [ 1 , m ] X_{i∈[1,m]} Xi∈[1,m]为输入
- X i X_i Xi分别乘上对应的权重wi得到 z i z_i zi
- 对 z i z_i zi求和
- 最后输入一个非线性(不是直线)的激活函数,得到最后的值 y ^ \hat{y} y^

为了提升感知机的表达性,我们可以在其中加入偏置( W 0 ( B i a s ) W_0(Bias) W0(Bias)),可以让激活函数向左或向右移动。
为什么要用激活函数
- 可以使网络变得非线性化,让网络拥有更强的拟合能力(因为数据多是非线性的,就像你不能用直线分开下图的红点跟绿点,但是非线性可以)
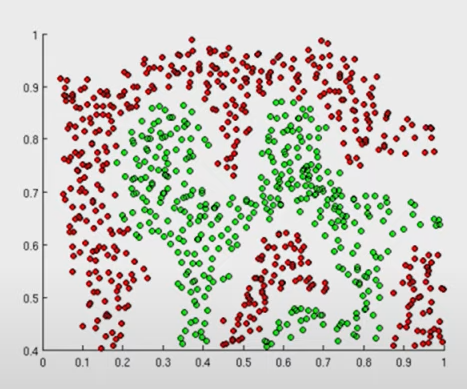

- 加快网络的训练
- 减少过拟合
两层感知机


多少个输出 y ^ \hat{y} y^就是多少层感知机。
图中的 z z z代表隐藏层,其输入激活函数sigmoid后就得到输出 y ^ \hat{y} y^
对于每一层的感知机都会有独立的偏置 w w w
其中的参数(权重,偏置),一开始都是随机初始化的(不能全部初始化为0),在后面的训练中不断更新改善参数。当然,也有初始化参数的方法,何凯明初始化等等,这里我就不一一赘述。
Loss 损失函数
然而,一开始搭建的网络并不能很好的用于预测的任务。因为它就像一个刚刚出生的孩子,对任何数据缺乏认识。所以我们应该指导这个孩子的学习,告诉他对错。而loss就是代表预测的错误程度。得到的loss越小,说明预测越接近真实。反之loss越大。
损失函数介绍的不是很详细,具体可以自行百度。
Empirical Loss

这是用于二元预测(是或不是)的一个损失函数。
这个损失函数输入的是预测(f(x))与真实(y)。最后算出每一层的loss,求和取平均得到 J ( W ) J(W) J(W)。

著名的交叉熵函数。

这个loss是用于预测多元的网络即输出的是考试的成绩而不是是否通过考试。
这个是计算预测与真实的距离(欧氏距离,类比一下二维中点的距离,以及三维中点距离的计算方式)
损失优化
对于网络参数的初始化,在没有规定的情况下都是随机初始化参数。
这里我们随机初始化了一个点。

然后我们基于loss对权重进行不断的迭代更新,直到找到最优的解(最低点)

利用loss优化
下面开始讲解如何利用损失进行优化。
我们知道,在二元函数中,我们可以通过计算出斜率(即函数的变化情况),进而知道接下来的函数的变化。故此,我们通过计算高维空间中的梯度(斜率),来更新到最优点。
- 初始化参数
- 计算梯度
- 更新权重(图中的 η η η是学习率,后面提到)
- 循环(第二步与第三步)
- 返回权重

我们来详细讲讲权重与最后的loss隔了那么远,是怎么通过梯度更新的(没学过高数的小伙伴,可以先了解一下偏导数,或者搜链式法则)。

由链式法则可以得 J ( w ) 与 w 1 J(w)与w_1 J(w)与w1的梯度。
带入梯度下降的公式:
W
⟵
W
−
η
∂
J
(
w
)
∂
w
W \longleftarrow W-\eta\frac{\partial J(w)}{\partial w}
W⟵W−η∂w∂J(w)
为了使梯度更新具有稳定性,防止梯度下降过快,所以引入了学习率η
学习率一般都设置的很小0.001之类的小数。
- 如果学习率太大,就会使梯度下降变得不可控,甚至无法是梯度进入最优点。
- 如果偏小,就会使网络更新的速度偏慢,训练过久。甚至陷入局部最优解。
局部最优解
下图是一个真实的loss降维后的可视化盆景:

我们可以看到,盆景中坑坑洼洼,凹陷处很多。那么我们在寻找最优解的时候很容易陷入局部最优。
目前有常见的两个方法解决这问题
idea 1
一个学习率不是适用于所有的网络
- 受梯度大小的影响
- 受学习发生的多快
- 权重的尺度大小
- 扥扥…
多次训练,尝试许多不同的学习率,找到最适合的那个。
idea 2
设计一种可以自动调整学习率的机制。
优化器变诞生了!!!

优化器也有许多种,我们应该了解不同优化器的利弊,已经其适用的条件环境。选择合适的优化器优化网络。
batch
训练网络要输入数据,如果一次只输入一份数据或一张图片,在梯度下降的时候,就充满不确定性。因为大量的数据集中总是存在着个例,梯度下降可能会受到特例的影响而偏离方向。为了保持网络的普遍性,所以我们要一次性输入一个批次的数据进行训练,在梯度下降的时候取均值。这样就具有了普遍的代表性。
W
⟵
W
−
1
B
∑
k
=
1
B
η
∂
J
(
w
)
∂
w
W \longleftarrow W-\frac{1}{B}\sum^B_{k=1}\eta\frac{\partial J(w)}{\partial w}
W⟵W−B1k=1∑Bη∂w∂J(w)
设置batch还可以让数据在多个设备,多个GPU上并行训练。
当然batch的尺寸大小也会影响网络,具体请自行百度。
过拟合
可以把网络理解为二维中的一个函数
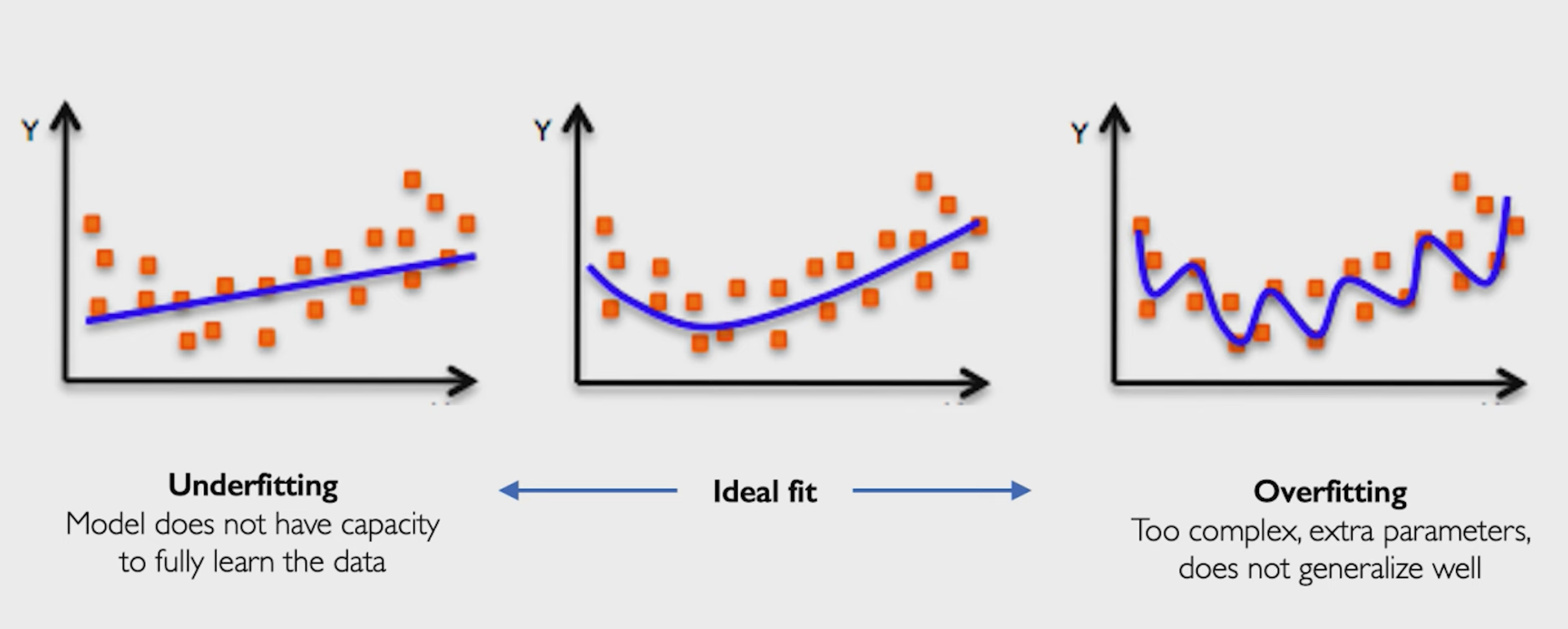
拟合,就是让这个函数可以表达出数据的特征

例如左边的图,就是训练不足,网络表达能力差。右边的图就拥有优秀的表达能力,曲线内的是绿类,外部是红类。
而过拟合就是这个网络在训练达到合适的阶段后继续多次训练,最后使函数的分布趋于训练集中数据。
但是训练集中的数据怎么能完全表达现实中的情况呢??
regularization
为了防止过拟合的出现,我们提出了正则化,让网络可以更好的拟合没有训练过的数据(提升鲁棒性)。
idea 1 Dropout
在训练的时候随机的使神经元断连(使其活性为0),在计算的时候不使用这个隐藏层。
认为,缺少神经元可以迫使网络更加努力的去学习数据的分布。
下图灰色的就是被断连的神经元。


假设我们使一半的神经断连,在训练一次后,我们就只训练另一半上传被断连的神经。为了使网络找到另一条寻找最优解的道路。
这个方法现在已经不用了,被Batch Normlization(Bn层)代替。
idea 2 早停法

用一个而外的test data 去验证网络的性能(计算loss),一直找到Testing Loss的最低点,那个时候的模型就是最好的。
已经不用了,被Batch Normlization(Bn层)代替。
idea 2 早停法

用一个而外的test data 去验证网络的性能(计算loss),一直找到Testing Loss的最低点,那个时候的模型就是最好的。
2021年8月7日18:16:05
持续更新……








 本文介绍了MIT的深度学习课程,重点讲解了单层和多层感知机的工作原理,包括激活函数的作用、损失函数及其优化。讨论了梯度下降法、局部最优解的问题以及解决策略,如学习率调整和优化器的选择。还提到了防止过拟合的正则化方法,如dropout和早停法,并简单探讨了批量训练的重要性。
本文介绍了MIT的深度学习课程,重点讲解了单层和多层感知机的工作原理,包括激活函数的作用、损失函数及其优化。讨论了梯度下降法、局部最优解的问题以及解决策略,如学习率调整和优化器的选择。还提到了防止过拟合的正则化方法,如dropout和早停法,并简单探讨了批量训练的重要性。
















 650
650

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








