无人机运动状态描述

坐标系

基本概念

直角坐标系

有X,Y,Z三个轴，相互正交（垂直）。

右手系

对直角坐标系X,Y,Z轴正方向的一种规定。右手拇指、食指、中指自然伸开呈相互正交。X轴，Y轴，Z轴反别为拇指、食指、中指方向。

惯性系

牛顿力学三定律在惯性系中成立。一般取地球面。

对地坐标系（GCS）

取地面一点为原点，取东方为X方向，北方为Y方向，右手系原则确定指向天空为Z轴方向（其实怎么选无所谓，只要是右手系就行，这里我就这么选）。设计这么一个坐标系的意义在于，可以假定地球是不动的，这样GCS就是固定的，其他变化的坐标系可以最后都转化到它这里进行融合。
这个坐标系下的坐标上标通常为E（earth）。

机体坐标系（BCS）

取机体一点为原点。右手系原则规定X,Y,Z轴方向（怎么方便怎么来）。设计这么一个坐标系的意义在于，方便进行受力分析。本项目采用B3坐标系。（根据怎么选X,Y,Z方向，坐标系分为B1,2,3。）

右手螺旋

右手四指握住一个坐标轴，大拇指指向坐标轴方向。则四指弯曲方向为绕该轴旋转的正方向。

旋转矩阵

$$\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right)$$
无人机的受力分析在机体坐标系进行，而最后的无人机姿态描述在对地坐标系进行。两个坐标系不统一，要怎么将一个坐标系的坐标向量转化为另一个坐标系的坐标向量呐？这就需要旋转矩阵了。他是这么用的：
$$r^B=C_E^B\times r^E$$
$$r^B=\left[\begin{array}{c}{x}^B\\ y^B\\ z^B\end{array}\right]$$
$$r^E=\left[\begin{array}{c}{x}^E\\ y^E\\ z^E\end{array}\right]$$
$C_E^B$呐，采用不同的旋转顺序会有不同。这里我采用航空次序欧拉角，即Z-Y-X次序欧拉角。这里你可能还不理解欧拉角还有这个旋转顺序，等一等。现让我把这个说完。航空次序欧拉角下， $C_E^B$为：
$$C_E^B=\left[\begin{array}{ccc}cos\theta cos\psi & cos\theta sin\psi & -sin\theta \\ sin\varphi sin\theta cos\psi -cos\varphi sin\psi & sin\varphi sin\theta sin\psi +cos\varphi cos\psi & sin\varphi cos\theta \\ cos\varphi sin\theta cos\psi +sin\varphi sin\psi & cos\varphi sin\theta sin\psi -sin\varphi cos\psi & cos\varphi cos\theta \end{array}\right]$$
$\psi$,$\theta$,$\varphi$分别为机体坐标系相当于对地坐标系绕Z轴旋转的角度、绕Y轴旋转的角度和绕X轴旋转的角度。
这样我们就实现了对地坐标系的坐标值向机体坐标系下的坐标值的映射。如果我们想反过来等式两边都左乘$C_E^B$的逆就好（我们把$C_E^B$的逆写为$C_B^E$）：
$$r^E=C_B^E\times r^B$$
如此，我们直接用这个旋转矩阵就可以了。但他是怎么来的呐？我们从二维的情况开始推导。

1. 首先我们假设有两个二维坐标系XOY和xoy。XOY不动，xoy绕他们共同的z轴转动。即刚开始连个坐标系是重合的，后来机体运动了，它俩就不重合了，找到两坐标系下坐标的关系就要找到两坐标系间的关系。
2. 如图，两坐标系间关系可以由转动角度$\theta$完全描述。
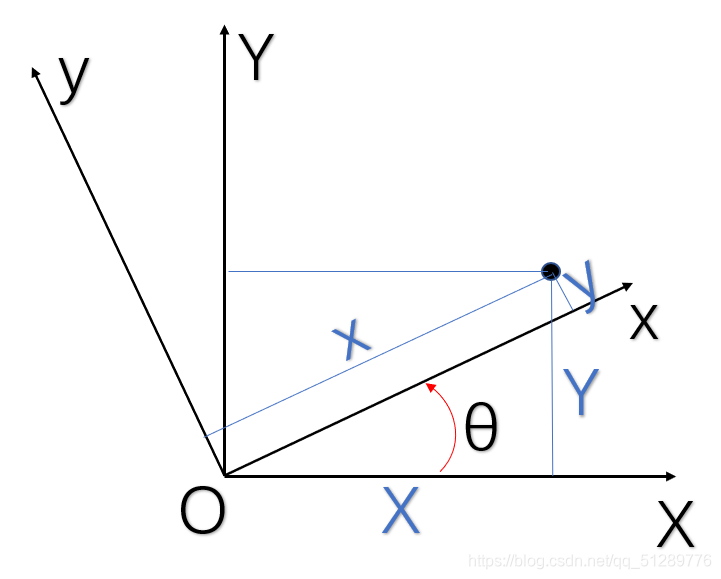
3. 简单推导可知：
   $$y=cos\theta \cdot (Y-X\cdot tan\theta )=-X\cdot sin\theta +Y\cdot cos\theta$$
   $$x=\frac{X}{cos\theta }+y\cdot tan\theta =X\cdot cos\theta +Y\cdot sin\theta$$
   矩阵形式：
   $$\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]\times \left[\begin{array}{c}X\\ Y\end{array}\right]$$
   二维情况下只需要一个旋转角就可以完全描述两个坐标系的关系。但三维情况下就需要三个旋转角了。我们称之为三个欧拉角，而这三个角改变的顺序的不同区分了不同的旋转矩阵。来看三维的情况：
4. 假设有两个二维坐标系OXYZ和Oxyz。OXYZ不动，Oxyz依次绕z,y,x轴转动（注意，此时绕的轴始终是机体坐标系的轴）。
5. 绕Z轴旋转$\psi$角。
   $$\left[\begin{array}{c}x1\\ y1\\ z1\end{array}\right]=\left[\begin{array}{ccc}cos\psi & sin\psi & 0\\ -sin\psi & cos\psi & 0\\ 0& 0& 1\end{array}\right]\times \left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$$
6. 绕Y轴旋转$\theta$角
   $$\left[\begin{array}{c}x2\\ y2\\ z2\end{array}\right]=\left[\begin{array}{ccc}cos\theta & 0& -sin\theta \\ 0& 0& 0\\ sin\theta & 0& cos\theta \end{array}\right]\times \left[\begin{array}{c}x1\\ y1\\ z1\end{array}\right]$$
7. 绕X轴旋转$\varphi$角
   $$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 0& cos\varphi & sin\varphi \\ 0& -sin\varphi & cos\varphi \end{array}\right]\times \left[\begin{array}{c}x2\\ y2\\ z2\end{array}\right]$$
8. 三个旋转矩阵相乘
   $$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 0& cos\varphi & sin\varphi \\ 0& -sin\varphi & cos\varphi \end{array}\right]\times \left[\begin{array}{ccc}0& 0& 0\\ 0& cos\varphi & sin\varphi \\ 0& -sin\varphi & cos\varphi \end{array}\right]\times \left[\begin{array}{ccc}cos\theta & 0& -sin\theta \\ 0& 0& 0\\ sin\theta & 0& cos\theta \end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=\left[\begin{array}{ccc}cos\theta cos\psi & cos\theta sin\psi & -sin\theta \\ sin\varphi sin\theta cos\psi -cos\varphi sin\psi & sin\varphi sin\theta sin\psi +cos\varphi cos\psi & sin\varphi cos\theta \\ cos\varphi sin\theta cos\psi +sin\varphi sin\psi & cos\varphi sin\theta sin\psi -sin\varphi cos\psi & cos\varphi cos\theta \end{array}\right]\times \left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$$

欧拉角

上问提到的三个角就是欧拉角，分别为$\psi$,$\theta$,$\varphi$。分别念psi,theta,phi。在无人机建模中，他们分别被称为偏航角YAW、俯仰角ROLL、滚转角（横滚角）PITCH。

补充

• 之前所提的航空次序欧拉角只是一种顺规而已。你可以发现很多种旋转次序都可以使一个坐标系旋转到任意位置。实际上只要满足这个条件就行：任何两次连续的旋转，必须绕着不同的旋转轴。共有12种合法顺规。而采取不同的顺规，对应的欧拉角肯定不同。只有欧拉角应用于惯性导航领域时，才称为偏航、俯仰、横滚角。
• 姿态除了可以用欧拉角表示，也可以用四元数表示。