文章介绍了如何利用位运算解决数组中的特定问题，如寻找唯一成对的数、找出落单的数、计算二进制中1的个数、判断整数是否为2的幂以及交换整数奇偶位等。通过多个实例展示了位运算在算法和编程中的巧妙应用。
目录
0.《算法很美》课程学习指导手册
略
1.1 课程介绍
略
1.2 题解：如何找数组中唯一成对的那个数
回顾：位运算奇巧淫技
/*位运算基础
* 位运算符
* 在处理整形数值时，可以直接对组成整形数值的各个位进行操作。这意味着
* 可以使用屏蔽技术获得整数中的各个位（? ?→)
* &(与)、|(或)、^(异或)、~(非/取反)
* >>和<<运算符将二进制位进行右移或者左移操作
* >>>运算符将用O填充高位;
* >>运算符用符号位填充高位，没有<<<运算符对于int型，1<<35与1<<3是相同的(35%32==3)
* 而左边的操作数是long型时需对右侧操作数模64
* 与:都为1结果为1，或:有一个为1结果为1，异或:二者不同时结果为1
*
* 位运算的奇巧淫技
* 判断奇偶数 x&1
* 获取二进制位是1还是0（两种解决方案) 移位 &1
* 交换两个整数变量的值
* 不用判断语句，求整数的绝对值
* 异或，可以理解为不进位加法∶1+1=0，0+0=0，1+0=1
* 性质
* 1、交换律可任意交换运算因子的位置，结果不变
* 2、结合律（即(a^b)^c == a^(b^c))
* 3、对于任何数x，都有x^x=0，x^0=x，同自己求异或为0，同0求异或为自己
* 4、自反性A^B^B=A^0=A，连续和同一个因子做异或运算，最终结果为自己
* */
//题解:如何找数组中唯─成对的那个数
/*题1:找出唯一成对的数
* 1-1000这1000个数放在含有1001个元素的数组中，
* 只有唯一的一个元素值重复，其它均只出现一次。
* 每个数组元素只能访问一次，设计一个算法，将它找出来;
* 不用辅助存储空间，能否设计一个算法实现?
* */
/*
* 思路：
* 利用异或的属性A^A=0;B^0=B;
* 将数组内所有数^(1^2...^1000)所得结果为重复的数
* */
package suanfahenmei;
import java.util.Random;
//1位运算
public class C1_2 {
public static void main(String[] args) {
// TODO 自动生成的方法存根
int N=1001;
int[] arr=new int[N];
for (int i = 0; i < arr.length-1; i++) {
arr[i]=i+1;
}
//前1000个数是1-1000不重复出现，最后一个数是随机数，范围是1到1000
arr[arr.length-1]=new Random().nextInt(N-1)+1;
//arr[arr.length-1]=new Random().nextInt(N);
//随机下标，然后与最后一个数交换顺序
int index=new Random().nextInt(N);
Util.swap(arr,index,arr.length-1);
Util.printArr(arr);
int x1=0;
for (int i = 1; i < N; i++) {
x1=x1^i;
}
for (int i = 0; i < N; i++) {
x1=x1^arr[i];
}
System.out.println(x1);
}
}
/*
* 还可以使用暴力破解法，
* 使用辅助数组,遍历原数组，
* 遇到几就在新数组相同下标加1，
* 元素值变为2的下标即为所求
* */
System.out.println("*****************");
int[] helper=new int[N];
for(int i=0;i<N;i++) {
helper[arr[i]]++;
if (helper[arr[i]]==2) {
System.out.println(arr[i]);
break;
}
} 1.3 找出落单的数，这样编程就对了
/*题2:找出落单的那个数
* 一个数组里除了某一个数字之外，
* 其他的数字都出现了两次。
* 请写程序找出这个只出现一次的数字。
* */
/*思路：基于1.2
* 全部异或，即可得出结果
* */
1.4 一题三解：二进制中1的个数
/*
* 题3:二进制中1的个数
* 请实现一个函数，输入一个整数，
* 输出该数二进制表示中1的个数。
* 例:9的二进制表示为1001，有2位是1
* 输出2
* */
/*思路1：
* 若32位二进制数，则循环32次，把1移位然后相与，再移回去，
* 把每次结果加起来。
* */
//思路1
Scanner sc=new Scanner(System.in);
int N=sc.nextInt();
System.out.println(Integer.toString(N,2));
int count=0;
//比对每一位
for (int i = 0; i < 32; i++) {
if ((N&(1<<i))==(1<<i)) {
count++;
}
}
System.out.println(count);思路2：也可以把原数字往后移，与1
/*思路3：
* 每次消除一个1，直到全部位为0，消除次数就是1的个数。
* 方法是不断减1再做&
* (x-1)&x可以消除最低位的1
* */
package suanfahenmei;
import java.util.Scanner;
public class C1_4 {
/*
* 题3:二进制中1的个数
* 请实现一个函数，输入一个整数，
* 输出该数二进制表示中1的个数。
* 例:9的二进制表示为1001，有2位是1
* */
//思路3
Scanner sc=new Scanner(System.in);
int N=sc.nextInt();
System.out.println(Integer.toString(N,2));
int count=0;
while (N!=0) {
N=(N-1)&N;
count++;
}
System.out.println(count);
}
}
1.5 一条语句判断整数是不是2的整数次方
/*
* 题4:是不是2的非负整数次方
* 用一条语句判断一个整数是不是2的整数次方。
* */
/*
* 思路：
* 2的整数次方的二进制只有一位是1其他全是0
* 基于上一个题，解此题即可
* */
package suanfahenmei;
import java.util.Scanner;
public class C1_5 {
public static void main(String[] args) {
// TODO 自动生成的方法存根
Scanner sc=new Scanner(System.in);
int N=sc.nextInt();
System.out.println(Integer.toString(N,2));
if (((N-1)&N)==0) {
System.out.println("是");
}
else {
System.out.println("否");
}
}
}
1.6 位运算思维：将整数的奇偶位互换
//题5:将整数的奇偶位互换
/*
* 思路1：for循环，i每次加2
* */
/*
* 思路2：
* 用1做&运算叫保留，用0做&叫消除
* */
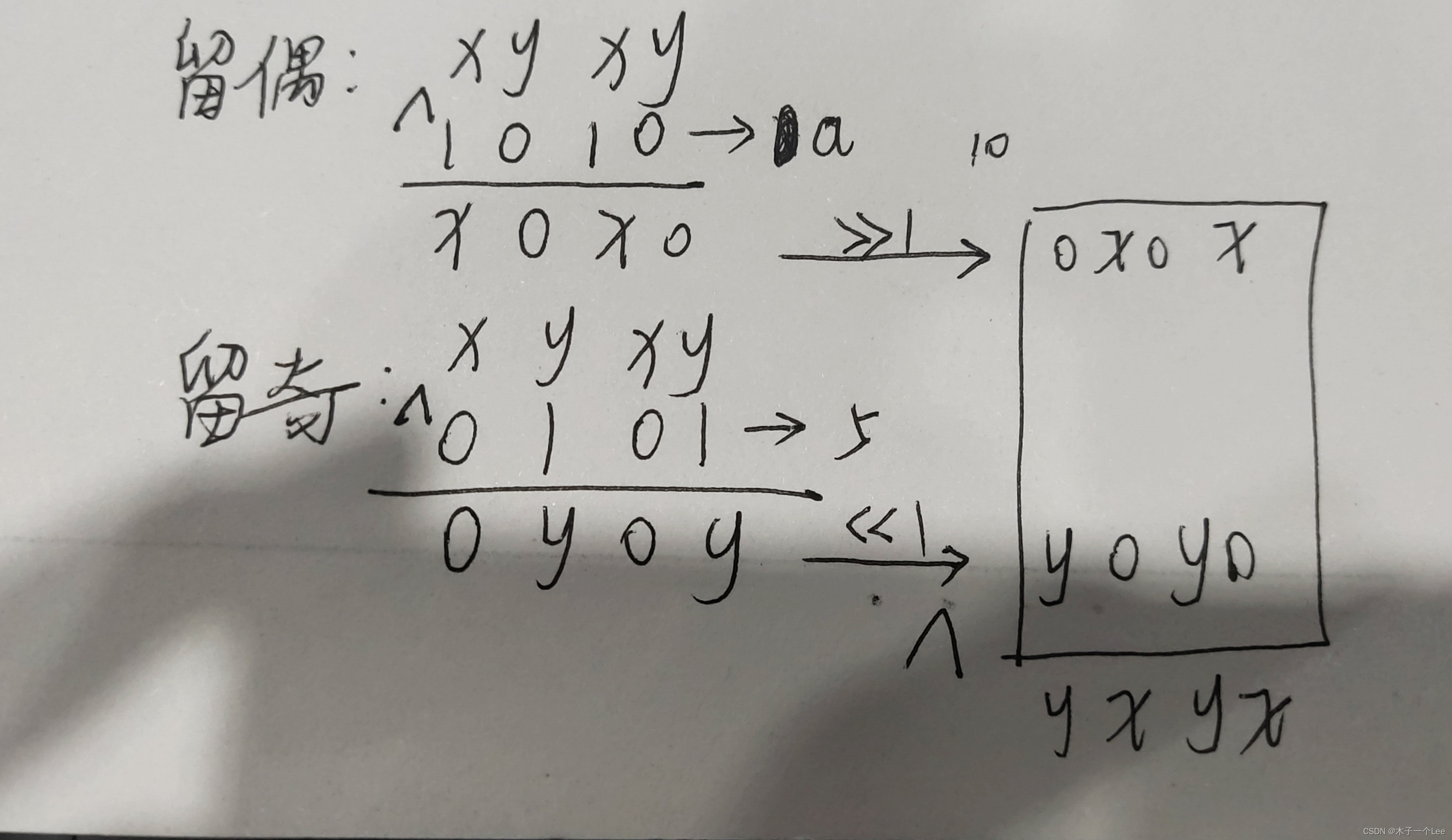这里只用思路2：
package suanfahenmei;
//import org.assertj.core.api.Assertions;
public class C1_6 {
public static void main(String[] args) {
// TODO 自动生成的方法存根
int a=6;
int b=m(9);
System.out.println(a==b);
//边界值
int c=0b01000000_00000000_00000000_00000000;//java8之后可以用_分隔二进制
int d=m(c);
System.out.println(d==0b10000000_00000000_00000000_00000000);
}
private static int m(int i) {//记从右往左第一位为第1个奇数位
int ou=i&0xaaaaaaaa;//和1010 1010 1010。。。做&运算取出偶数位
int ji=i&0x55555555;//和0101 0101 0101。。。做&运算取出奇数位
return (ou>>1)^(ji<<1);//连起来
}
}
1.7 乘2挪整：二进制表示浮点实数
/*
* 题6: O~1间浮点实数的二进制表示
* 给定一个介于O和1之间的实数，（如0.625)，类型为double,
* 打印它的二进制表示(0.101，
* 因为小数点后的二进制分别表示0.5,0.25.0.125......) 。
* 如果该数字无法精确地用32位以内的二进制表示，则打印“ERROR”
* */
/*
* 思路：不断乘2
* */
package suanfahenmei;
public class C1_7 {
public static void main(String[] args) {
// TODO 自动生成的方法存根
double num=0.625;
StringBuilder sb=new StringBuilder("0.");//一个可变的字符序列
while (num>0) {
double r=num*2;
//判断整数部分
if (r>1) {
sb.append("1");
//消除整数部分
num-=r-1;
}
else {
sb.append("0");
num=r;
}
if (sb.length()>34) {//小数点以及小数点前的0加上32位就是34位
System.out.println("ERROR");
return;
}
}
System.out.println(sb.toString());
}
}
1.8、1.9 编程实践：出现k次与出现1次
/*
* 题7:出现k次与出现1次
* 数组中只有一个数出现了1次，
* 其他的数都出现了k次，
* 请输出只出现了1次的数。
* */
/*
* 思路1：利用数组计数
* */
/*
* 思路2：
* 不进位加法
* 2个相同的2进制数做不进位加法，结果为0
* 10个相同的10进制数做不进位加法，结果为0
* k个相同的k进制数做不进位加法，结果为0
*
* 1.把所有数转换为k进制：
* ·手工取余法
* ·Integer.toString(i.radix);
* 2.然后做k进制不进位加法，
* ·取余
* ·逢k-k
* 3.把最后结果还原为原来的数
* */
这里使用思路2：
package suanfahenmei;
public class C1_8and9 {
public static void main(String[] args) {
// TODO 自动生成的方法存根
int[] arr= {2,2,2,9,7,7,7,3,3,3,6,6,6,0,0,0};
int len=arr.length;
char[][] kRadix=new char[len][];
int k=3;
//转换成k进制字符串数组
int maxlen=0;
//对于每个数字
for (int i = 0; i < len; i++) {
//求每个数字的三进制字符串并翻转(为了从低位对齐)，然后转换为字符数组
kRadix[i]=new StringBuilder(Integer.toString(arr[i], k)).reverse().toString().toCharArray();
if (kRadix[i].length>maxlen) {
maxlen=kRadix[i].length;//记录最长三进制的位数，为了逐位相加
}
}
int[] resArr=new int[maxlen];
for (int i = 0; i < len; i++) {//遍历每一行
//不进位加法：按位相加再取余
for (int j = 0; j < maxlen; j++) {//遍历每一列
if (j>=kRadix[i].length) {
resArr[j]+=0;
}
else {
resArr[j]+=(kRadix[i][j]-'0');
}
}
}
int res=0;
for (int i = 0; i < maxlen; i++) {//resArr存每一位加起来的和
res+=(resArr[i]%k)*(int)(Math.pow(k,i));
}
System.out.println(res);
}
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
