课堂练习(一)

1.计算真正率和真假率

法一(不放心就用这种方法，一步一步来)：
先画出混淆矩阵：

再利用公式求解：

 

得出真正例率TPR=7/(7+3)=0.7，假例率TPR=4/(4+6)=0.4

法二(一眼丁真法)：直接看图中的结局

真正率是截断点以及以上的1除以所有1
假正率是截断点以及以上的0除以所有0

2.求支持度和置信度

计算示例：

本题解法：

求支持度找面包和牛奶同时出现的次数，求置信度还需要前者(面包)的出现次数
则支持度=3/5=0.6

置信度=0.6/(4/5)=0.75

3.Apriori算法求频繁项集

 步骤：

 ​​​​

 原理与特点：

项集（水果）是频繁的（对身体有益）

子集（苹果，梨）是频繁的（对身体有益）

公鸡不是鸟，鸡肯定不是鸟

 

 

 

4.基于Hash(散列)的计数求解频繁二项集 

大致步骤：

 

基本原理与特点、举例：

 

 

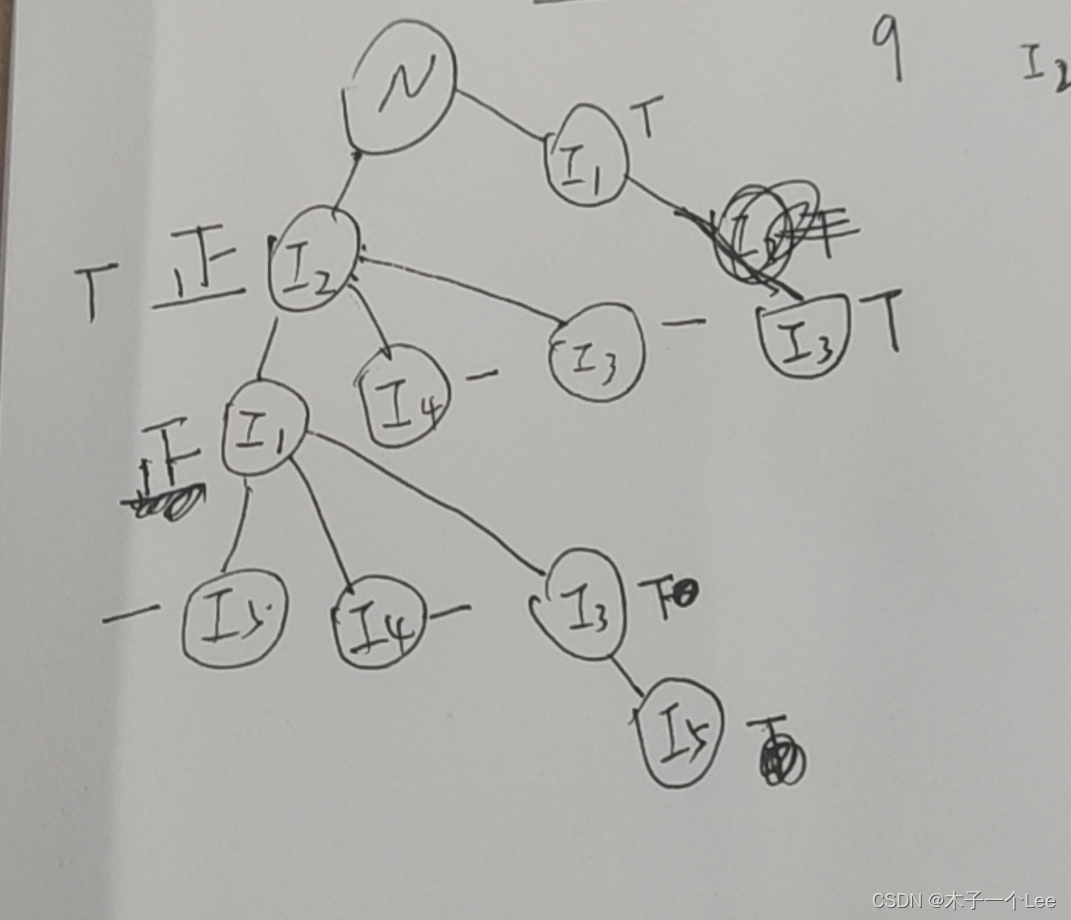
5.构造FP树：

1. 支持度排序： 扫描一次数据集，确定每个项的支持度计数。丢弃非频繁项， 而将频繁项按照支持度的递减排序。 L = {a:8, b:7, c:6, d:5, e:3}

2. 构建 FP 树： 第二次扫描数据集，读入第一个事务 {a, b} 之后，创建标记为 a 和 b 的结点。然后形成

       null->a->b路径。该路径所有结点的频度计数为1。

    

     读入第二个事务{b,c,d}之后，为项b,c和d创建新的结点集。然后，连接结点null->b->c->d，形成一条代表该事务的路径。该路径上的每个结点的频度计数也等于1.

      注意：尽管前两个事务具有一个共同项b，但是它们的路径不相交，因为这两个事务没有共同的前缀.

 

 

 

 

也可以画正字