排序算法：堆排序，快速排序，归并排序。内附完整代码和算法思路详解。

目录

一：堆排序

1.1：堆的数据结构

1.2：大小根堆

1.3：向下调整算法构建小根堆

1.4：堆排序思想

二：快速排序

2.1：快排单趟思想

三：归并排序

3.1：分组过程

3.2：归并过程

---

一：堆排序

1.1：堆的数据结构

堆必须是一颗完全二叉树。逻辑结构如下：（当然它也可以是一颗满二叉树）

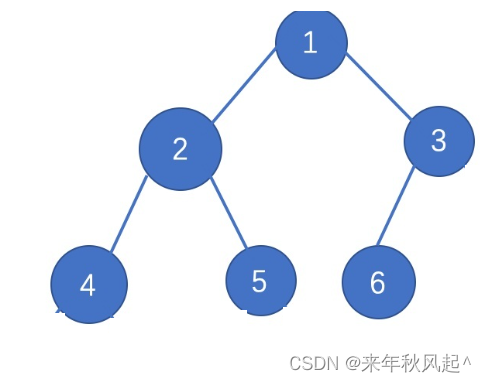
实际的存储结构如下：

 

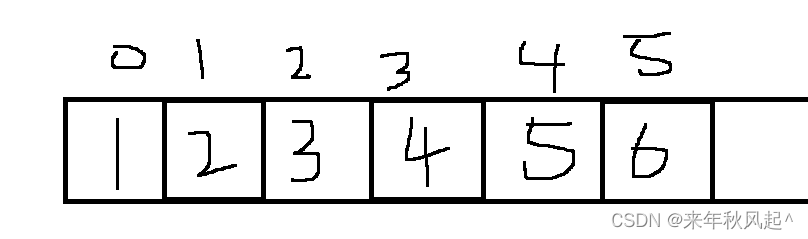
那我们在数组中去表示这颗完全二叉树时，有两个基本公式，

根据自身下标位置，推导孩子的下标位置。

当本身的下标为 i 时，那么这个节点的左孩子下标为 i*2+1，右孩子的下标节点为 i*2+2;

根据自身下标位置，推导父亲的下标位置。

当本身的下标为 i 时，父亲的下标为 （i - 1）/ 2；

这两个公式是非常重要的，可以说堆排序就是依托着这两个公式存在的。

1.2：大小根堆

大根堆：每一颗子二叉树都必须满足 ：根值大于等于左孩子值，根值大于等于右孩子值

小根堆：每一颗子二叉树都必须满足 ：根值小于等于左孩子值，根值小于等于右孩子值

上面的图正好是一个小根堆。

1.3：向下调整算法构建小根堆

void ADjustDowld(int* a, int n, int root)
{
	int parent = root;
	int child = parent * 2 + 1;

	while (child < n)
	{
		if (child + 1 < n && a[child + 1] < a[child]) {
            //当右孩子值比左孩子还要小，那就让child+1.保证处理后child指向最小的那个孩子
			child++;
		}

		if (a[child] < a[parent]) {
			int tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}

}

思想：我们单看一颗二叉树来说，先找出它左右两个孩子中较小的那个值的下标，然后呢，我们让较小的那个孩子与他的父亲的值进行比较，让较小的那个值去当根。这里就把这一颗二叉树构建成小根堆了。

所以为了构建整棵树的小根堆，我们从最下面的那个根节点开始。

通过数组下标我们可以得到最后一个数据的下标为 i = n -1 ，那么他的根节点的下标就是 （n-1）/ 2；

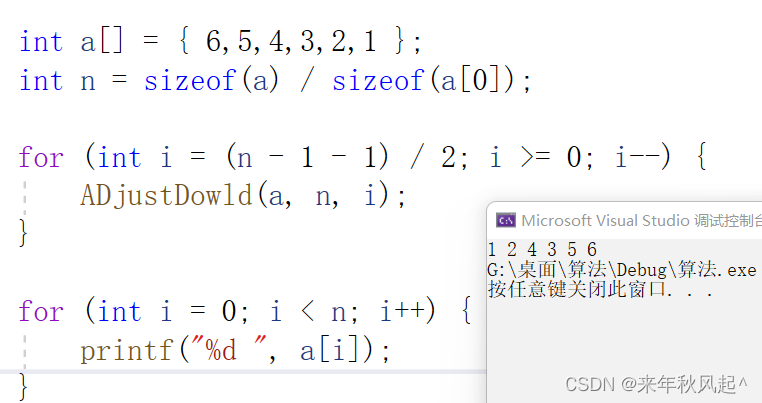
可以看到，经过我们的向下调整算法后，我们以及把这个堆构建成一个小根堆了， 

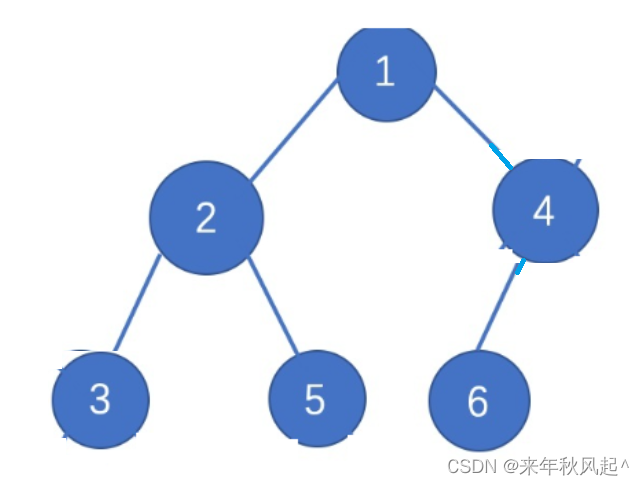
对于每一个子二叉树来说，它们都满足小根堆的定义，根值小于等于左孩子值，根值小于等于右孩子值

1.4：堆排序思想

有了前面的先导知识，我们就知道了，堆呢每次只可以选出一个极值，那我们要怎么使用这个算法对数组进行排序呢，这里我们又有了两个定义：

排升序，定义大根堆（每次选出最大值，和最后一位数据进行交换，然后让数组的长度减一）

排降序，定义小根堆（每次选出最小值，和最后一位数据进行交换，然后让数组的长度减一）

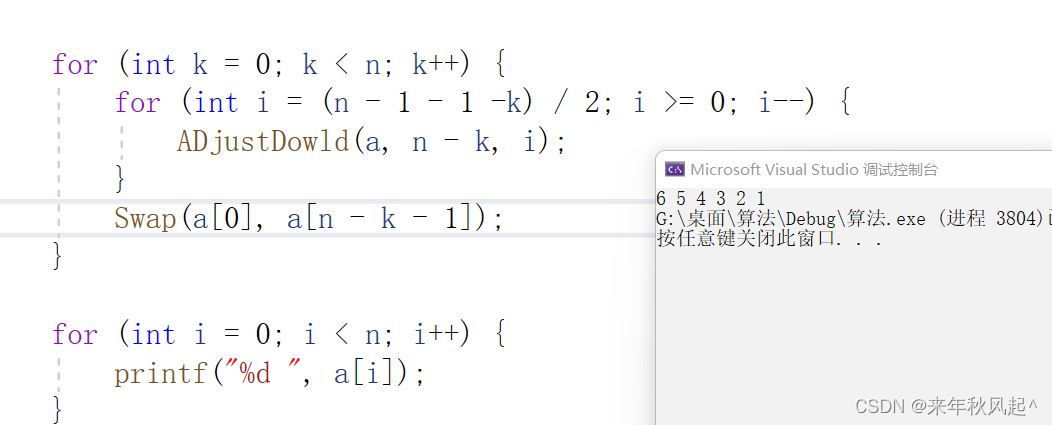
这里呢只对排降序进行了实现，如果要使用堆排升序，也是一样的。只需要修改一下向下调整算数中的条件即可。

二：快速排序

2.1：快排单趟思想

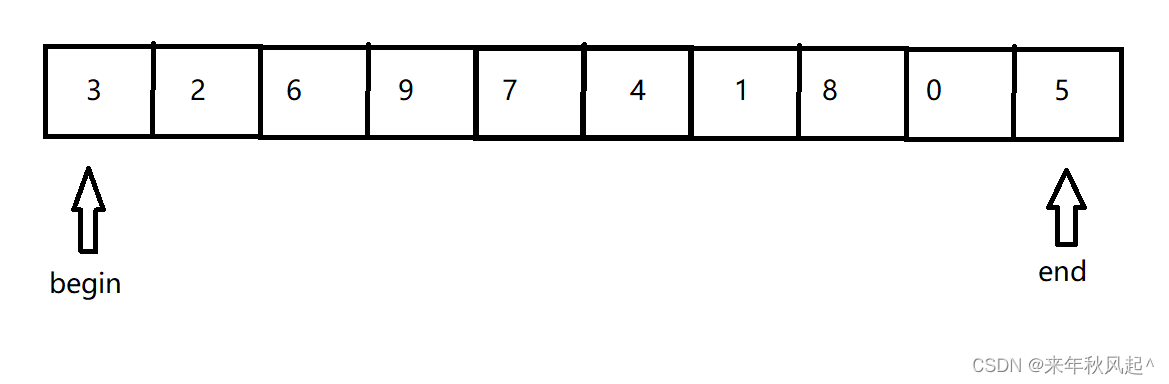
 我们使用两个指针，分别指向数组的第一个节点和最后一个节点，然后我们选择一个来当起始点，（这里我们选择end作为起始点），我们记录下end节点的下标，然后让begin指针先走（如果我们选择的是begin为起始点，那么就得让end指针先走）

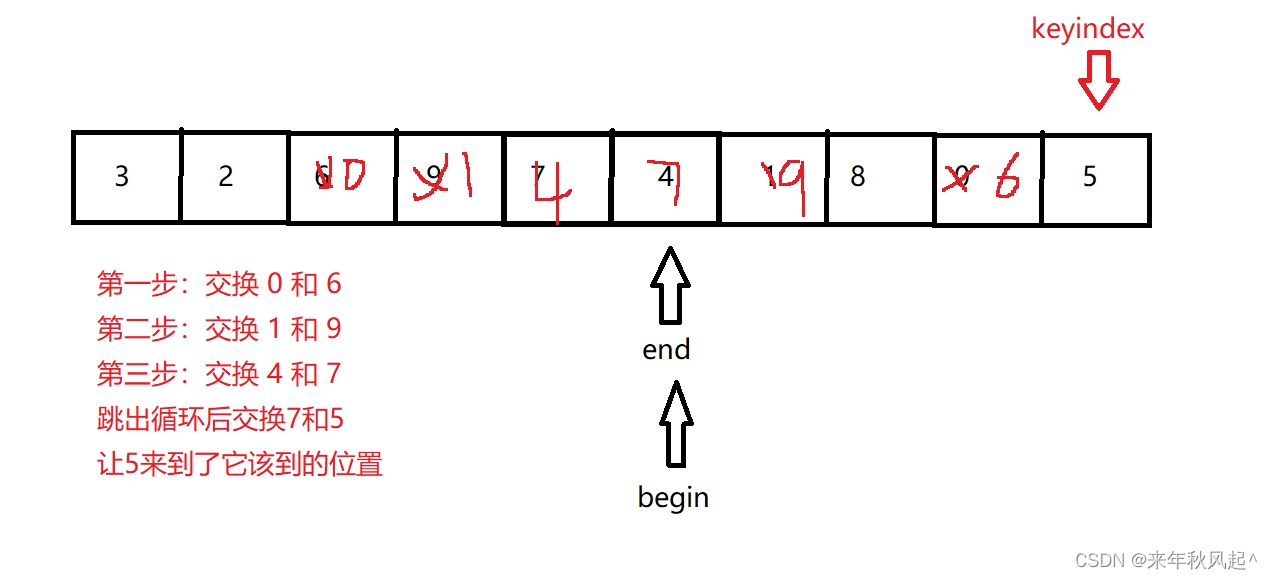
这里我们就能让每次选出的keyindex的值来到它该到的下标位置，并且左边都是比a[keyindex]要小的，右边都是比a[keyindex]要大的。

那么我们只需要不断递归，就能完成排序。实现代码如下：

int parentSort(int* a, int begin, int end)
{
	int keyindex = end;
	while (begin < end) {
		while (begin < end && a[begin] <= a[keyindex]) {
			++begin;
		} //出来后，a[begin] > temp

		while (begin < end && a[end] >= a[keyindex]) {
			--end;
		} // 出来后，a[end] < temp;
		Swap(a[begin], a[end]);
	}
	Swap(a[end], a[keyindex]);
	return end;
}

void qSort(int* a, int left, int right)
{
	if (left >= right) {
		return;
	}

	int div = parentSort(a, left, right);
	qSort(a, left, div - 1); //排自己左边
	qSort(a, div + 1, right);//排自己右边
}

void test02()
{
	int a[] = { 6,5,4,3,2,1 };
	int n = sizeof(a) / sizeof(a[0]);
    
	qSort(a, 0, n - 1);

	for (int i = 0; i < n; i++) {
		printf("%d ", a[i]);
	}
}

三：归并排序

归并排序的中心思想就是通过不断的分组，分组到最后每个组只有一个数据，那么就可以开始归并排序了。

3.1：分组过程

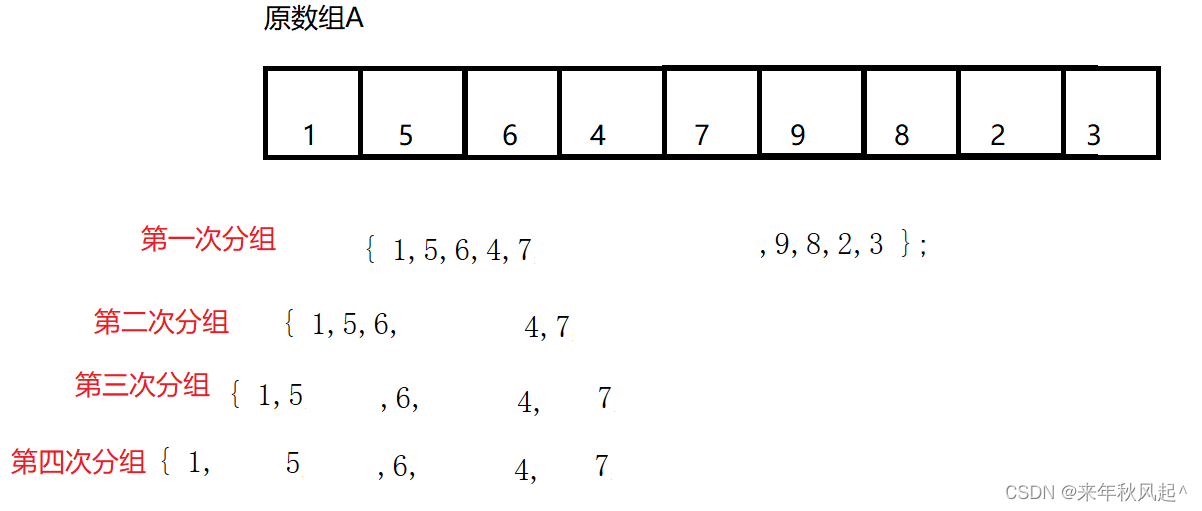
他会通过递归将数据不断分组，分到最后数据不能再分割的时候，就开始进行归并了。 

3.2：归并过程

 第一次归并1和5，使得1，5有序，

第二趟归并1，5，6，使得1，5，6，有序。

第三趟归并4，7，使得4，7，有序。

第二趟归并1，5，6，和4，7使得1，4，5，6，7，有序。

（这里只列举了左边的归并过程，右边的也同理，当然这个顺序是归并到临时数组中，最后有序了，再拷贝回原数组中）

/* 归并排序 */
void _MergeSort(int* a, int left, int right, int* tmp)
{
	if (left >= right) { //不能再进行分组了
		return;
	}

	int mid = left + (right - left) / 2;
	//[left, mid] [mid+1, right]分组,有序即可排序，无序，分出子问题

	_MergeSort(a, left, mid, tmp);
	_MergeSort(a, mid + 1, right, tmp);

	//归并[left, mid][mid+1, right]有序
	int begin1 = left; int end1 = mid;
	int begin2 = mid + 1; int end2 = right;
	int index = begin1;

	while (begin1 <= end1 && begin2 <= end2) {
		if (a[begin1] <= a[begin2])
			tmp[index++] = a[begin1++];
		else
			tmp[index++] = a[begin2++];
	}

	while (begin1 <= end1)//begin2走完了
		tmp[index++] = a[begin1++];

	while (begin2 <= end2)//begin1走完了
		tmp[index++] = a[begin2++];

	//将归并好顺序的tmp中的数据都拷贝回a中。
	for (int i = left; i <= right; i++) {
		a[i] = tmp[i];
	}
}

void MergeSort(int *a, int n)
{
	if (a == NULL) {
		return;
	}

	int* tmp = (int*)malloc(sizeof(int) * n);
	_MergeSort(a, 0, n - 1, tmp);

	free(tmp);
}