【第一章】-MATLAB Simulink概述
【例 1-1】
计算 y=3cos(π/3)+1235+29 y = \frac{3\cos (\pi /3) + 12^3}{5 + \sqrt{29}} y=5+293cos(π/3)+123
clc; % 清除屏幕
y = (3 * cos(pi / 3) + 12^3) / (5 + sqrt(29)) % 公式转换为函数
输出结果为:
y =
166.5356
其中pi表示π\piπ,sqrt()是求平方根函数,^表示求幂运算
【例 1-2】
保存命令save和导入命令load的使用
x = [0:0.1:5];
y = cos(x);
save filexy x y % 把变量x, y存入filexy.mat文件中
z = 'Hello World' % 把字符串赋值给z变量
% 把变量追加存入filexy.mat文件中
save filexy z -append
clear
load filexy
save filexy -ascii
【例 1-3】
针对二阶系统被控对象的状态控件传递函数:
A=[−3−10010],B=[10],C=[0100],D=0 A = \begin{bmatrix} -3 & -100 \\ 1 & 0 \end{bmatrix}, B = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, C = \begin{bmatrix} 0 & 100 \end{bmatrix}, D = \bold{0} A=[−31−1000],B=[10],C=[0100],D=0
要求:输出原系统的阶跃响应曲线,并搭建PID负反馈控制系统,通过试凑KpK_pKp、KiK_iKi、KdK_dKd参数,分别在示波器和工作控件输出阶跃响应曲线和数据
如下图所示为原系统的仿真结构
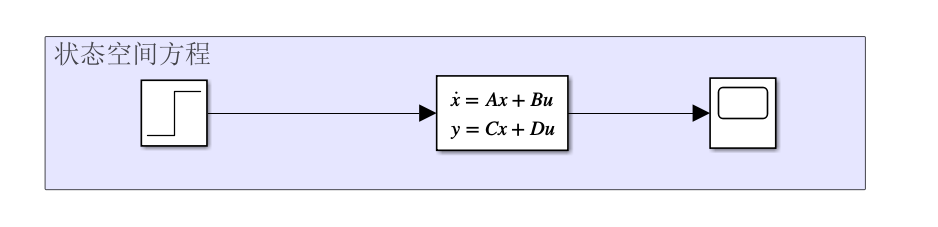
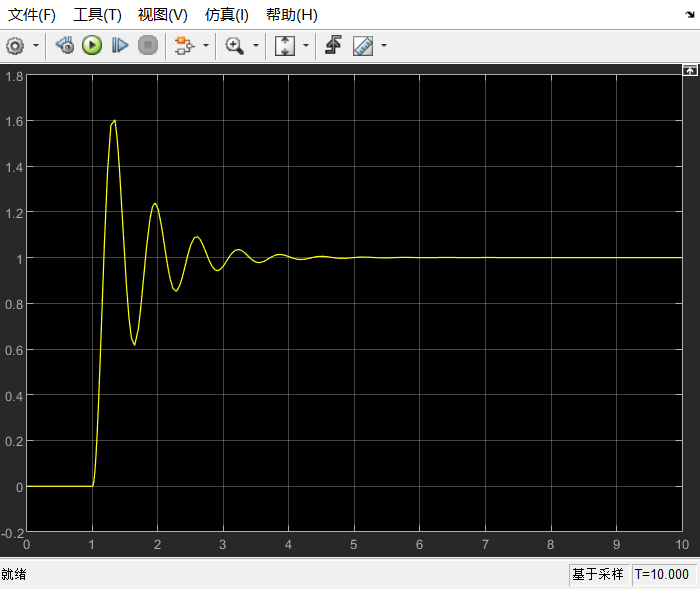
原二阶系统的仿真曲线为
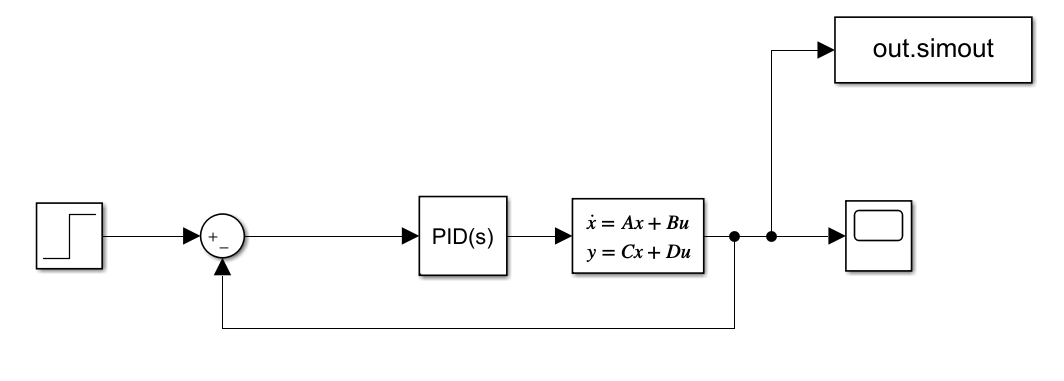
加入PID控制后,Simulink仿真结构为
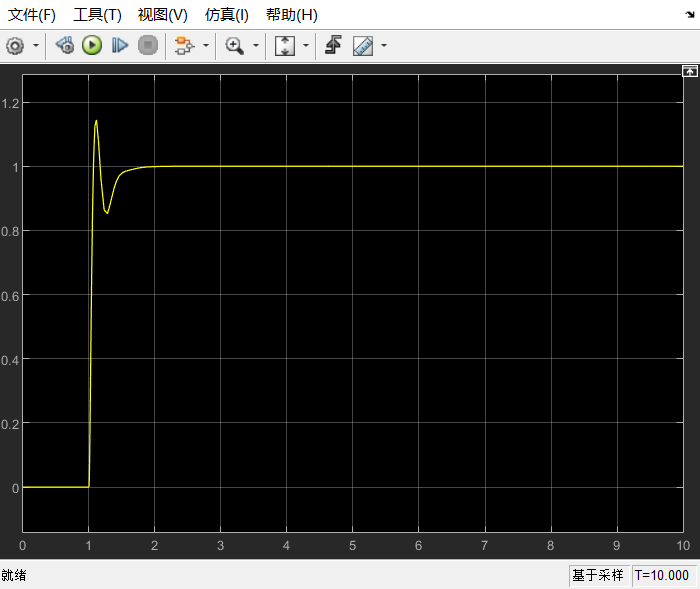
仿真曲线为
【例 1-4】
使用Simulink创建微分方程模型
x¨=2u(t)+3x+4x˙\ddot{x} = 2u(t) + 3x + 4\dot{x} x¨=2u(t)+3x+4x˙
通过仿真观察输出结果
如下图所示为微分方程结构图
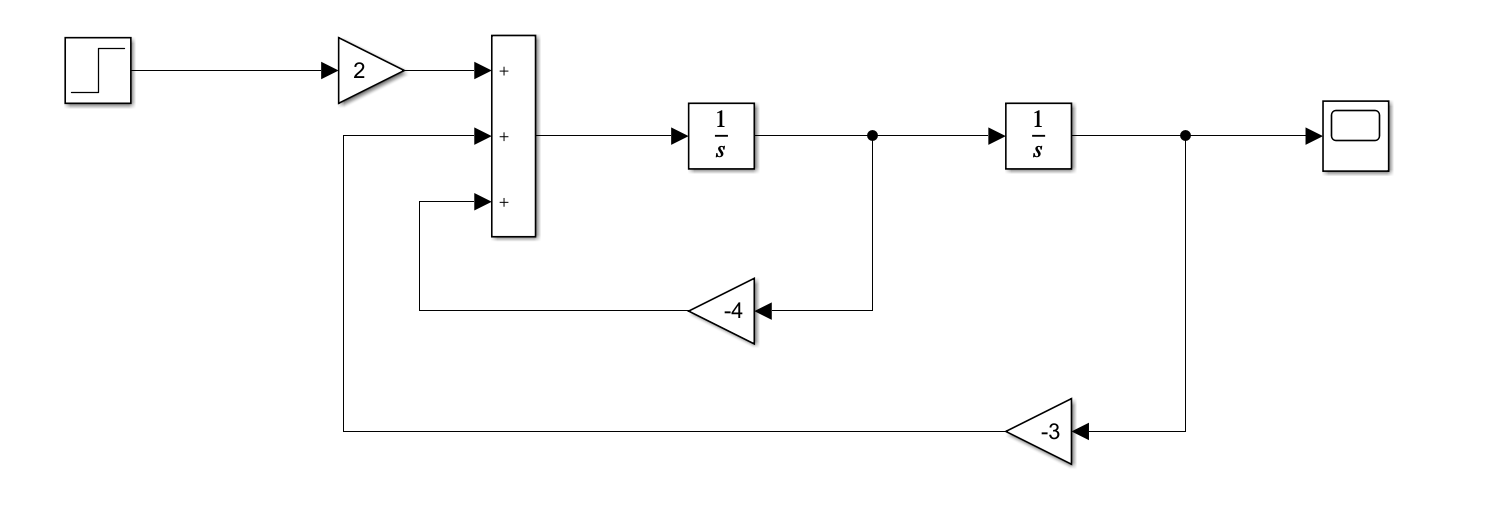
点击运行(Run)按钮后双击示波器即可观察到该模型的输出结果
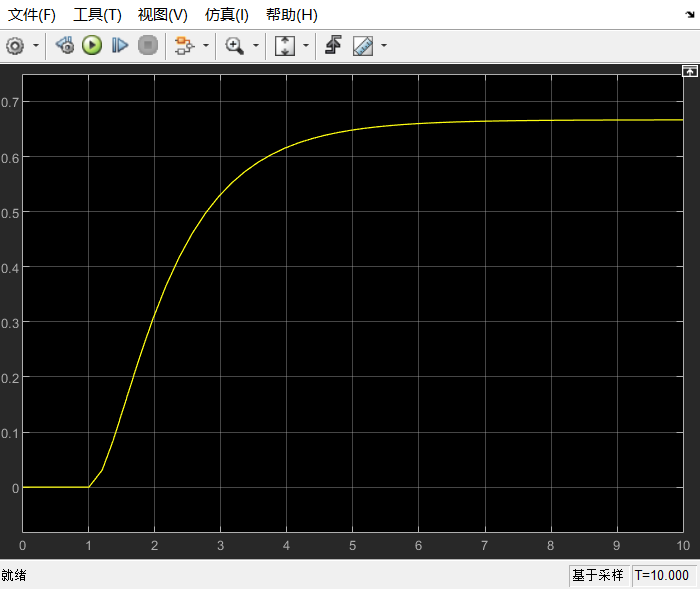
从图像上可以得到,该系统是个稳定系统具有较好的动态特性
参考链接
控制系统建模与仿真 基于MATLAB/Simulink的分析与实现 姜增如 清华大学出版社





















 3630
3630

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








