03变换（二维与三维）

GAMES101: 现代计算机图形学入门

GAMES101_Lecture_03

缩放：

反转:

切变：

x'=x+ay

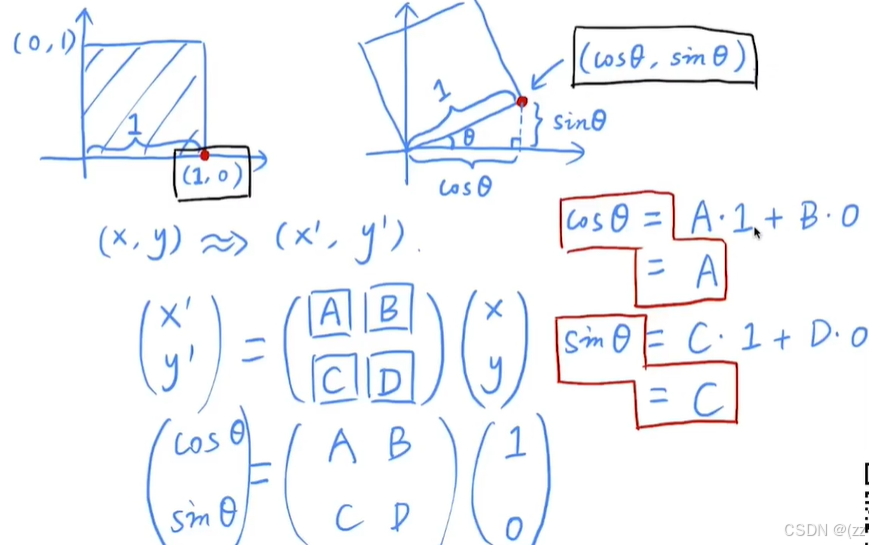
旋转：

以（0，0）为中心，默认逆时针

边长为1，（1，0）（cosθ，sinθ）

引入齐次坐标：

因为平移要加减，所以引入齐次坐标

点+1，向量+0

平移：

为什么向量是0：向量具有平移不变性

向量(x,y,0)经过平移变换矩阵（如上图左矩阵）后应还是(x,y,0)

点（x，y，1）-点（u，v，1）=（x-u，y-v，0）是一个向量

点+点=这两个点的中点

点+点后除w（如上图所示）

齐次下总结：

分解，注意旋转是以原点为中心，矩阵是从右往左相乘

理解：矩阵乘法不能改变顺序

任意点为中心旋转分解：

3维空间：

顺序：先线性再平移

下图是先线性再平移

 

矩阵结构，矩阵中的平移分量位于第四列，当执行矩阵乘法时，这相当于在应用线性变换后加上平移量。例如，矩阵中的tx会乘以齐次坐标的1，然后加上到x'的计算中，即x' = ax + by + c*z + tx。这说明线性变换（a,b,c作用于x,y,z）之后再加上tx，所以顺序是先线性变换，再平移。

当计算新坐标时，线性变换部分先作用于原坐标 (x, y, z)，随后平移分量 (t_x, t_y, t_z) 被直接叠加到结果上。例如：

x' = a·x + b·y + c·z + t_x
y' = d·x + e·y + f·z + t_y
z' = g·x + h·y + i·z + t_z