基础 DP 之硬币问题

最新推荐文章于 2025-04-13 08:35:58 发布

不负她所期

最新推荐文章于 2025-04-13 08:35:58 发布

阅读量963

点赞数 3

分类专栏：基于Java的代码及算法文章标签：算法动态规划 java

本文链接：https://blog.youkuaiyun.com/qq_50811909/article/details/109118731

版权

基于Java的代码及算法专栏收录该内容

15 篇文章

订阅专栏

动态规划

动态规划（Dynamic Programming），简称 DP

算法思想： DP 问题一般是多阶段决策问题，把一个复杂的问题分解为相对简单的子问题，再一个个解决，最后得到复杂问题的最优解；这些子问题是前后相关的，并且非常相似，处理方法几乎一样。把前面子问题的计算结果记录为“状态”，并存储在“状态表”中，后面子问题可以直接查找前面得到的状态表，（即用前面子问题的结果推导后续子问题的解）避免了重复计算，极大地减少了计算复杂度

求解 DP 问题有 3 步，即 定义状态、状态转移、算法实现。核心是 状态、状态转移方程（递推方程）。用状态转移方程求解状态，状态往往就是问题的解。

DP 是一种常用的算法思想，时间效率高，代码量少

最少硬币问题

问题描述

有 n 种硬币，面值分别为 v1,v2,……vn，数量无限。输入非负整数 s ，选用硬币，使其和为 s，要求输出最少硬币组合的数量

解题思路

定义一个数组 int Min[MONEY]，其中 Min[i] 是金额 i 对应的最少硬币数量。如果程序能计算出 Min[i],0< i <MONEY，那么对输入的某个金额 i，只要查 Min[i] 就得到了答案
如何计算 Min[i]? Min[i] 和 Min[i-1] 是否有关系？

下面以 5 种面值（1、5、10、25、50）的硬币为例讲解递推的过程
（1）只使用最小面值的 1 分硬币。初始值 Min[0] = 0，其他的 Min[i] 为无穷大，如下图所示。下面计算 Min[1]。

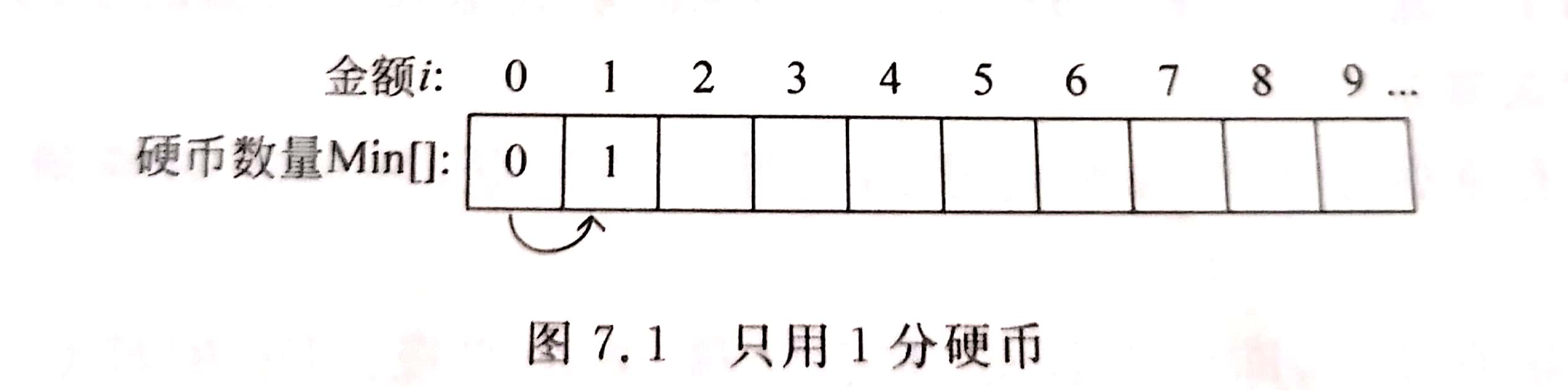
i=0, Min[0] = 0, 表示金额为 0。在这个基础上加一个 1 分硬币，就前进到金额 i=1、硬币数量 Min[1] = Min[0] + 1 = Min[1-1] + 1 = 1 的情况。
同理，i=2 时，相当于在 Min[1] 的基础上加一个硬币，得到 Min[2] = Min[2-1] + 1 = 2。继续这个过程，结果如下图所示。

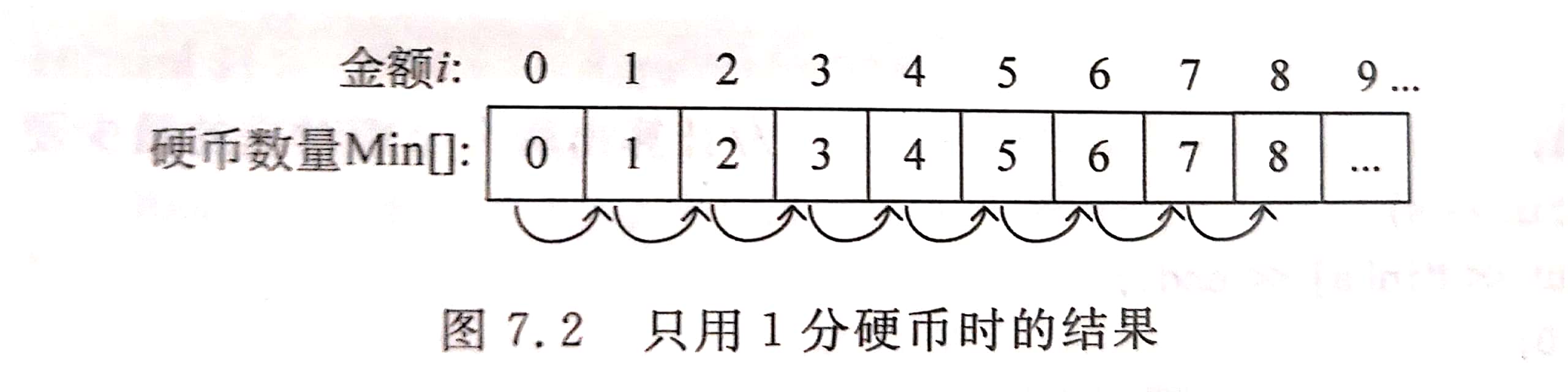
分析上述过程，得到递推关系 Min[i] = min( Min[i], Min[i-1]]+1)
（2）在使用 1 分硬币的基础上增加使用第二大面值的 5 分硬币，如下图所示。此时，应该从 Min[5] 开始，因为比 5 分小的硬币金额不可能用 5 分硬币实现。

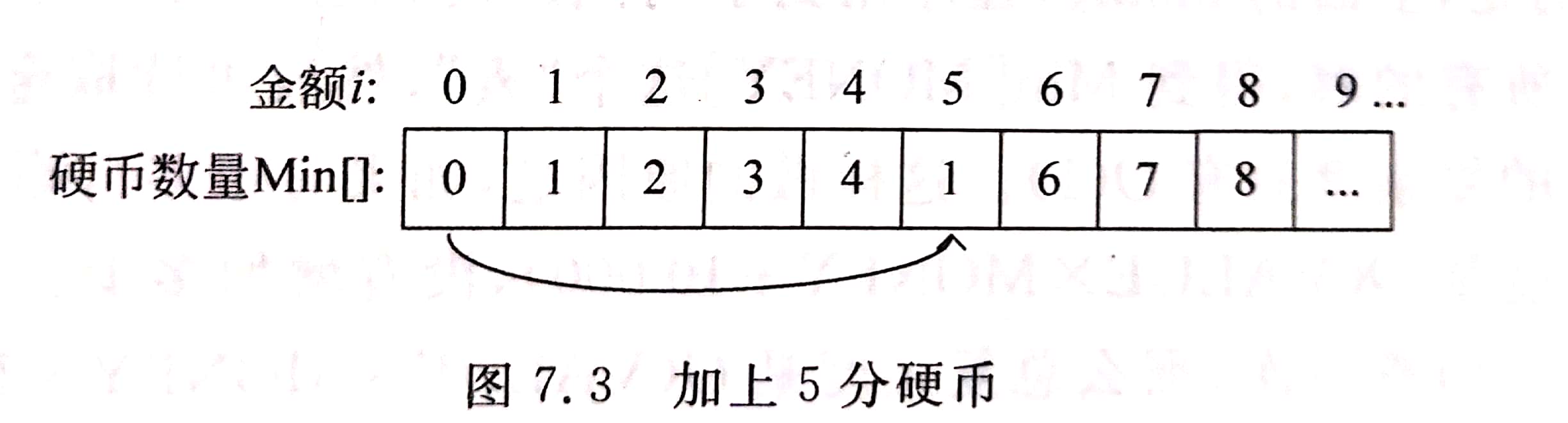
    i=5 时，相当于在 i=0 的基础上加一个 5 分硬币，得到 Min[5] = Min[5-5] + 1 = 1。上一步用 1 分硬币的方案有 MIn[5] = 5。取最小值，得 Min[5] = 1
    同理，i=6 时，有 Min[6] = Min[6-5] + 1 = 2, 对比原来的 Min[6] = 6, 取最小值。
    继续这个过程，结果如下图所示

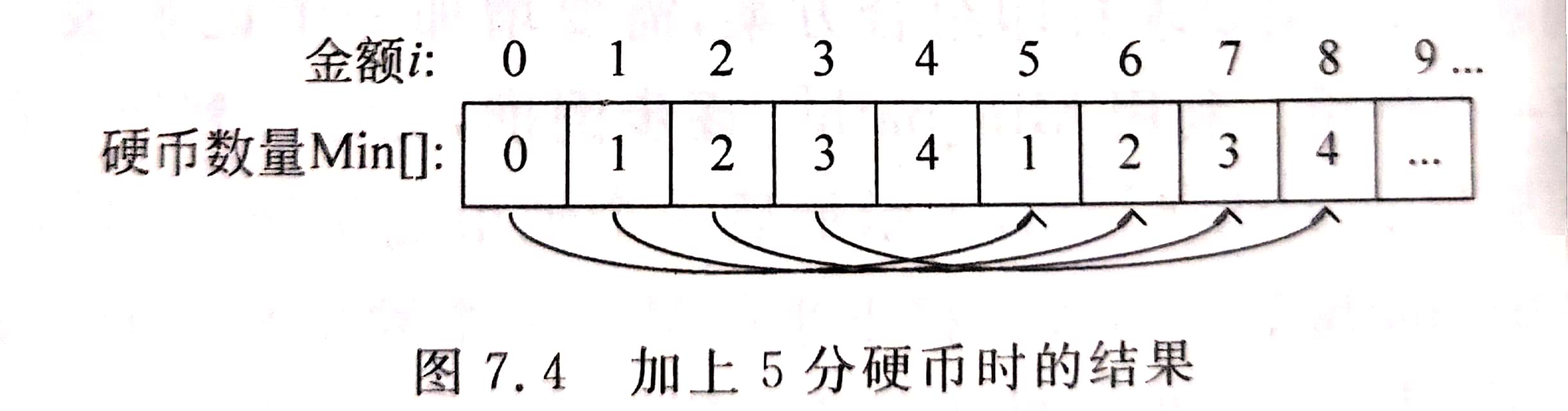
（3）继续处理其他面值的硬币

上述思路的 代码如下（Java）

import java.util.*;

public class Main
{
    final int MONEY = 251;   //定义最大金额
    final int VALUE = 5;   //举例 5 种硬币
    int[] type = {1, 5, 10, 25, 50};   //5 种面值
    int[] Min = new int[MONEY];  //每个金额对应最少的硬币数量

    private void solve(){
        for(int i=0; i<MONEY; i++)   //初始值为无穷大
            Min[i] = Integer.MAX_VALUE;
        Min[0] = 0;
        for(int j=0; j<VALUE; j++){
            for(int i=type[j]; i<MONEY; i++){
                Min[i] = Math.min(Min[i], Min[i-type[j]]+1);   //递推式
            }
        }
    }

    public static void main(String args[]){
        int s;
        Main m = new Main();
        m.solve();  //计算出所有金额对应的最少硬币数量，打表
        Scanner sc = new Scanner(System.in);
        while (!sc.hasNext("#")){ //以 # 字符串结束输入
           s = Integer.valueOf(sc.nextLine());
           System.out.println(m.Min[s]);
        }
    }
}

注意：上面的程序用到了“打表”的处理方法，即在输入金额之前提前用 solve() 算出所有的解，得到 Min[MONEY] 这个表，然后再读取金额 s ，查表直接输出结果，查一次表的复杂度只有 O(1) 。这样做的原因：如果有很多测试数据，例如 10000 个，那么总复杂度是 O(VALUE * MONEY + 10000)，（solve() 的复杂度是O(VALUE * MONEY），没有增加多少。如果不打表，每次读一个 s，就用 solve() 算一次，那么总复杂度是 O(VALUE * MONEY * 10000)，时间几乎多了 1 万倍

打印最少硬币的组合

解题思路

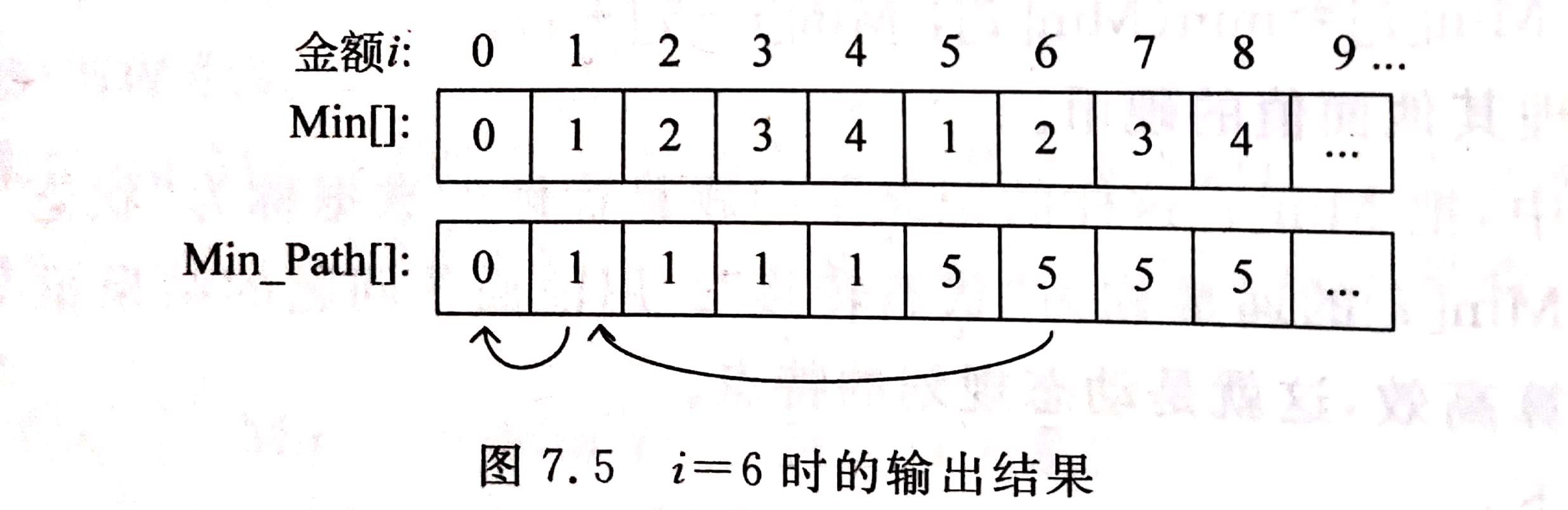
在最少硬币问题中，如果要求打印组合方案，需要增加一个记录表 Min_path[i]，记录金额 i 需要的最后一个硬币。利用 Min_path[] 逐步倒退，就能得到所有的硬币
例如，金额 i=6 ，Min_path[6]=5，表示最后一个硬币是 5 分；然后，Min_path[6-5]=Min_path[1]，查 Min_path[1]=1，表示接下来的最后一个硬币是 1 分；继续 Min_path[1-1]=0，不需要硬币了，结束。输出结果如下图所示，硬币组合是“ 5分+ 1分”

代码如下（Java）

public class Main
{
    final int MONEY = 251;   //定义最大金额
    final int VALUE = 5;   //举例 5 种硬币
    int[] type = {1, 5, 10, 25, 50};   //5 种面值
    int[] Min = new int[MONEY];   //每个金额对应的最少的硬币数量
    int[] Min_path = new int[MONEY];   //记录最小硬币的路径

    private void solve(){
        for(int i=0; i<MONEY; i++)
            Min[i] = Integer.MAX_VALUE;
        Min[0] = 0;
        for(int j=0; j<VALUE; j++){
            for(int i=type[j]; i<MONEY; i++){
                if(Min[i] > Min[i-type[j]]+1) {
                    Min_path[i] = type[j];   //在每个金额上记录路径，即每个硬币的面值
                    Min[i] = Min[i - type[j]] + 1;   //递推式
                }
            }
        }
    }

    private void print_ans(int s){   //打印硬币组合
        while (s !=0){
            System.out.print(Min_path[s]+" ");
            s -= Min_path[s];
        }
        System.out.print('\n');
    }

    public static void main(String args[]){
        int s;
        Main m = new Main();
        m.solve();
        Scanner sc = new Scanner(System.in);
        while (!sc.hasNext("#")){ //以 # 字符串结束输入
           s = Integer.valueOf(sc.nextLine());  
           System.out.println(m.Min[s]);   //输出最少硬币个数
           m.print_ans(s);   //打印硬币组合
        }
    }
}

所有硬币组合

问题描述

解题思路

（1）不完全解决方案
假设硬币数量不限，即题中没有 num<=100 的限制
定义一个记录状态的数组 int dp[251]。dp[i] 表示金额 i 所对应的组合方案数，即解空间。找到 dp[i] 和 dp[i-1] 的递推关系，就能高效地解决问题。

    第一步：只用 1 分硬币进行组合
    dp[0] = 1 为初始值
    dp[1] 可以从 dp[0] 推导出来：当金额 s=1 时，如果用一个 1 分硬币，等价于从 s 中减少 1 分钱，并且硬币数量也减少一个的情况。此时退到 i=0；如果 i=0 存在组合方案，那么 i=1 的组合方案也存在。dp[1] = dp[1] + dp[0]
    对于其他的 dp[i] ，同样有 dp[i] = dp[i] + dp[i-1]。（理解：右边的 dp[i] 是不使用 1 分硬币时的前一种状态，dp[i-1] 是总额减少 1 分时的前一种状态，左边即是得到一种新状态）
    在上述中，dp[i] 是“状态”，dp[i] = dp[i] + dp[i-1] 是状态转移方程。前面子问题的状态 dp[i-1] 和 dp[i]，用状态转移方程计算后，得到后面子问题的状态 dp[i]
    计算可得下表（只用 1 分硬币时）

i	0	1	2	3	4	5	6	7	8	…
dp[i]	1	1	1	1	1	1	1	1	1	…

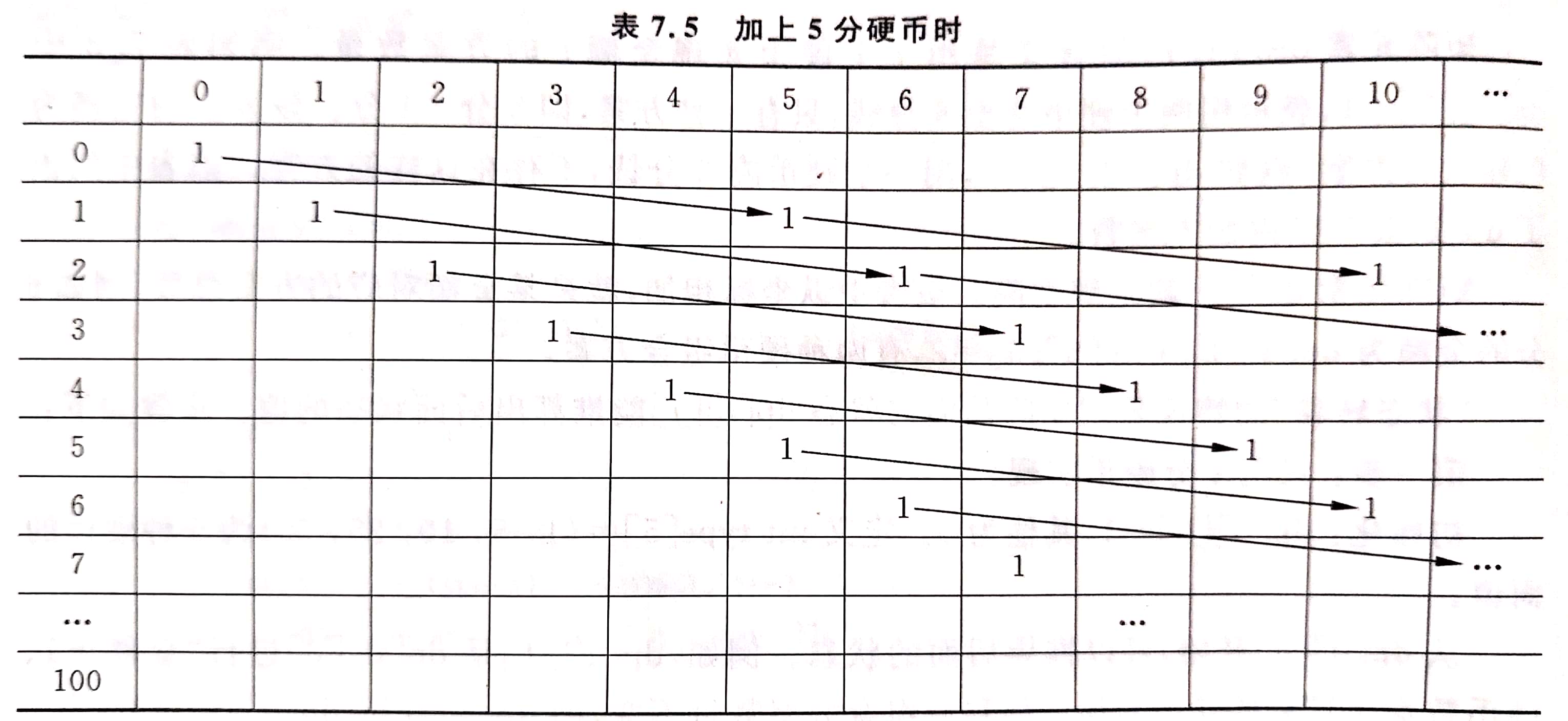
    第二步：加上 5 分硬币，继续进行组合
    当 i<5 时，组合中不可能有 5 分硬币
    当 i>=5 时，金额为 s 时的组合数量等价于从 s 中减去 5，而且硬币数量减去 1 个的情况
    dp[i] = dp[i] + dp[i-5]（理解：右边的 dp[i] 是不使用 5 分硬币时的前一种状态，dp[i-5] 是总额减少 5 分时的前一种状态，左边即是得到一种新状态）
    计算可得下表（加上 5 分硬币时）

i	0	1	2	3	4	5	6	7	8	…
dp[i]	1	1	1	1	1	2	2	2	2	…

第三步：继续处理 10 分、25 分、50 分硬币的情况，同理有 dp[i] = dp[i] + dp[i-10]、dp[i] = dp[i] + dp[i-25]、dp[i] = dp[i] + dp[i-50]

在上述步骤中，一次计算的复杂度只有 O(1)，全部计算的复杂度只有 O(ks)，k 是不同面值硬币的个数，s 是最大金额

代码如下（Java）

import java.util.*;

public class Main
{
    final int MONEY = 251;   //定义最大金额
    int[] type = {1, 5, 10, 25, 50};  //5 种面值
    int[] dp = new int[MONEY];

    private void solve(){
        dp[0] = 1;
        for(int i=0; i<5; i++)
            for(int j=type[i]; j<MONEY; j++){
                dp[j] = dp[j] + dp[j-type[i]];   //递推式
            }
    }

    public static void main(String args[]){
        int s;
        Main m = new Main();
        m.solve();   //提前计算出所有金额对应的组合数量，打表
        Scanner sc = new Scanner(System.in);
        while (!sc.hasNext("#")){ //以 # 字符串结束输入
           s = Integer.valueOf(sc.nextLine());
           System.out.println(m.dp[s]);
        }
    }
}

（2）完全解决方案
考虑到 num<=100，重新定义状态为 dp[i][j]，建立一个“转移矩阵”，如下表所示。其中横向是金额（题中 i<=250）,纵向是硬币数（题中最多用 100 个硬币，j<=100）

j/i	0	1	2	3	4	5	6	7	8	9	10	…
0	1
1		1				1
2			1				1				1
3				1				1				…
4					1				1
5						1				1
6							1				1
7								1				…
…									…
100

矩阵元素 dp[i][j] 的含义是用 j 个硬币实现金额 i 的方案数量。例如上表格中 dp[6][2] = 1，表示用两个硬币凑出 6 分钱，只有一种方案，即 5分+ 1分。该表格中的空格为 0，即表示没有方案。
矩阵 dp[][] 就是解空间。该表中纵坐标相加，就是某金额对应的方案总数，例如 6 分的金额为 dp[6][2] + dp[6][6] = 2，有两种硬币组合方案

    第一步：只用 1 分硬币实现
    初始化： dp[0][0] = 1, 其他为 0。定义 int type[5] = { 1, 5, 10, 25, 50 }为 5 种硬币的面值
    从 dp[0][0] 开始，可以推导后面的状态。例如，dp[1][1] 是 dp[0][0] 进行“金额+1、硬币数量+1”后的状态转移
    考虑到 dp[1][1] 原有的方案数，递推关系修正为：
dp[1][1] = dp[1][1] + dp[0][0] = dp[1][1] + dp[1-1][1-1] = 0+1 =1

dp[1-1][1-1] 的意思是从 1 分金额中减去 1分硬币的钱，原来 1 个硬币的数量也减少 1 个。

    在操作中，上述操作写成：
    dp[1][1] = dp[1][1] + dp[ 1-type[0] ][1-1]
    对所有 dp[i][j] 进行上述操作，结果如下图所示

    第二步：加上 5 分硬币，继续进行组合
    dp[i][j] ,当 i<5 时，组合中不可能有 5 分硬币
    当 i>=5 时，金额为 i、硬币为 j 个的组合数量等价于 从 i 中减去 5 分钱，而硬币数量也减去 1 个（即这个面值 5 的硬币） 的情况。dp[i][j] = dp[i][j] + dp[i-5][j-1] (= dp[i][j] + dp[ i-type[1] ][j-1])。对所有 dp[i][j] 进行上述操作，结果如下所示

第三步：陆续加上 10 分、25 分、50 分硬币，同理得到以下关系：
dp[i][j] = dp[i][j] + dp[ i-type[k] ][j-1], k=2, 3, 4

总结上述过程，算法的总复杂度为 O(kmn)，k 是不同面值硬币的个数，m 和 n 是矩阵的大小

代码如下（Java）

import java.util.*;

public class Main
{
    final int COIN = 101;   //题目要求不超过 100 个硬币
    final int MONEY = 251;   //题目给定的钱数不超过 250
    int[] type = {1, 5, 10, 25, 50};   //5 种面值
    int[][] dp = new int[MONEY][COIN];   //DP 转移矩阵

    private void solve(){   //DP
        dp[0][0] = 1;
        for(int i=0; i<5; i++)
            for(int j=1; j<COIN; j++)
                for(int k=type[i]; k<MONEY; k++){
                dp[k][j] += dp[k-type[i]][j-1];
            }
    }

    public static void main(String args[]){
        int s;
        Main m = new Main();
        Scanner sc = new Scanner(System.in);
        int[] ans = new int[m.MONEY];
        m.solve();   //用 DP 计算完整的转移矩阵
        for(int i=0; i<m.MONEY; i++)  //对每个金额计算有多少种方案，打表
            for(int j=0; j<m.COIN; j++)   //从 0 开始，注意 dp[0][0]=1
                ans[i] += m.dp[i][j];
        while (!sc.hasNext("#")){ //以 # 字符串结束输入
           s = Integer.valueOf(sc.nextLine());
           System.out.println(ans[s]);
        }
    }
}