Jansen 2020 Machine Learning for Al Chapter 9代码复现（二）

四、绘制移动平均值和标准差

        定义函数TestStationaryPlot来检验序列的平稳性。

def TestStationaryPlot(ts):
    rol_mean = ts.rolling(window = 12, center = False).mean()
    rol_std = ts.rolling(window = 12, center = False).std()
    plt.plot(ts, color = 'blue',label = u'原始数据')
    plt.plot(rol_mean, color = 'red', linestyle='-.', label = u'移动平均')
    plt.plot(rol_std, color ='black', linestyle='--', label = u'标准差')
    plt.xticks(fontsize = 25)
    plt.yticks(fontsize = 25)
    plt.xlabel(u'时间（年）', fontsize = 25)
    plt.ylabel(u'价格', fontsize = 25)
    plt.legend(loc='best', fontsize = 18)
    plt.title(u'移动平均和标准差', fontsize = 27)
    plt.show(block= True)

 五、ADF检验

       

定义TestStationaryAdfuller函数，对序列进行ADF检验。 

def TestStationaryAdfuller(ts, cutoff = 0.01):
    ts_test = adfuller(ts, autolag = 'AIC')
    ts_test_output = pd.Series(ts_test[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
    for key,value in ts_test[4].items():
        ts_test_output['Critical Value (%s)'%key] = value
    print(ts_test_output)
    if ts_test[1] <= cutoff:
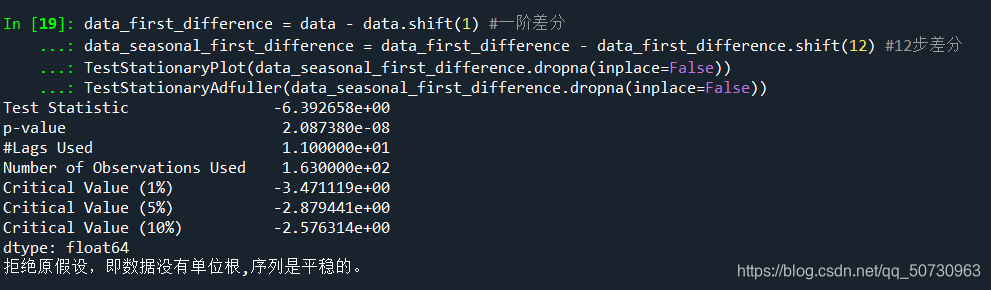
        print(u"拒绝原假设，即数据没有单位根,序列是平稳的。")
    else:
        print(u"不能拒绝原假设，即数据存在单位根,数据是非平稳序列。")

 结果为：

六、序列平稳化

        对原始的序列作1阶12步差分来提取原序列的趋势效应和季节效应

data_first_difference = data - data.shift(1) #一阶差分
data_seasonal_first_difference = data_first_difference - data_first_difference.shift(12) #12步差分  
TestStationaryPlot(data_seasonal_first_difference.dropna(inplace=False))
TestStationaryAdfuller(data_seasonal_first_difference.dropna(inplace=False))

差分后的序列图及检验结果如下

 

 七、白噪声检验

#白噪声检验
data_seasonal_first_difference.dropna(inplace = True)
r,q,p = sm.tsa.acf(data_seasonal_first_difference.values.squeeze(), qstat=True) 
data = np.c_[range(1,41), r[1:], q, p] 
table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"]) 
print(table.set_index('lag'))

             AC          Q  Prob(>Q)
lag                                
1.0   0.134548   3.222653  0.072626
2.0  -0.057476   3.814125  0.148516
3.0  -0.084782   5.108603  0.164015
4.0   0.020234   5.182766  0.269053
5.0  -0.030606   5.353444  0.374284
6.0  -0.050748   5.825469  0.443023
7.0  -0.036542   6.071665  0.531407
8.0  -0.088600   7.527678  0.480911
9.0   0.024161   7.636606  0.571141
10.0  0.060250   8.318058  0.597800
11.0  0.021679   8.406821  0.676464
12.0 -0.451548  47.153245  0.000004
13.0 -0.141176  50.964087  0.000002
14.0 -0.032962  51.173120  0.000004
15.0  0.032890  51.382538  0.000007
16.0  0.088978  52.924864  0.000008
17.0  0.026148  53.058906  0.000014
18.0  0.068606  53.987511  0.000018
19.0  0.067750  54.898894  0.000024
20.0 -0.008665  54.913899  0.000042
21.0  0.051037  55.437822  0.000061
22.0 -0.050116  55.946305  0.000087
23.0 -0.068516  56.902939  0.000106
24.0 -0.114977  59.614739  0.000072
25.0  0.077896  60.867741  0.000079
26.0  0.092983  62.665093  0.000073
27.0  0.021314  62.760171  0.000113
28.0 -0.083681  64.235713  0.000114
29.0  0.011723  64.264871  0.000177
30.0 -0.011195  64.291645  0.000270
31.0 -0.077984  65.599812  0.000281
32.0  0.028559  65.776476  0.000401
33.0 -0.003386  65.778978  0.000594
34.0  0.110049  68.439499  0.000419
35.0 -0.004910  68.444834  0.000614
36.0  0.100167  70.680700  0.000488
37.0 -0.044029  71.115823  0.000628
38.0 -0.082991  72.673049  0.000598
39.0 -0.016350  72.733935  0.000840
40.0  0.021184  72.836899  0.001153

白噪声检验结果可知，1阶12步差分后的序列延迟1-12期时，Q统计量的P值均小于0.01，所以在0.01的显著性水平下，拒绝原假设，即1阶12步差分后的序列是非白噪声序列