树的数据结构详解-优快云博客

本文详细介绍了树的概念，包括树的定义、结点类型、结点之间的关系，如根结点、子树、叶子结点、分支结点、双亲、孩子、堂兄弟和祖先等。此外，还阐述了树的层次、深度、有序树以及森林的定义。通过对这些概念的解析，读者可以深入理解树这一重要的数据结构。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在这里插入图片描述

树的定义：
什么是一棵树？
树(Tree)是n(≥0)个结点的有限集合。n = 0时，称为空树。在任意一棵非空树中：
(1) 有且仅有一个特定的称为根(Root)的结点；(2)当n > 1时, 其余n-1个结点
可分为m(m>0)个互不相交的有限集T1、T2、T3……Tm，其中每一个集合本身又是一棵树，并且是根的子树

    总结：（1）树的每一个结点是一个有序集合，每一个集合也是一棵树，称为子树
         （2）当结点数量为0时，那么称为空树
         （3）对于任何非空树中，任何树只能存在一个根结点

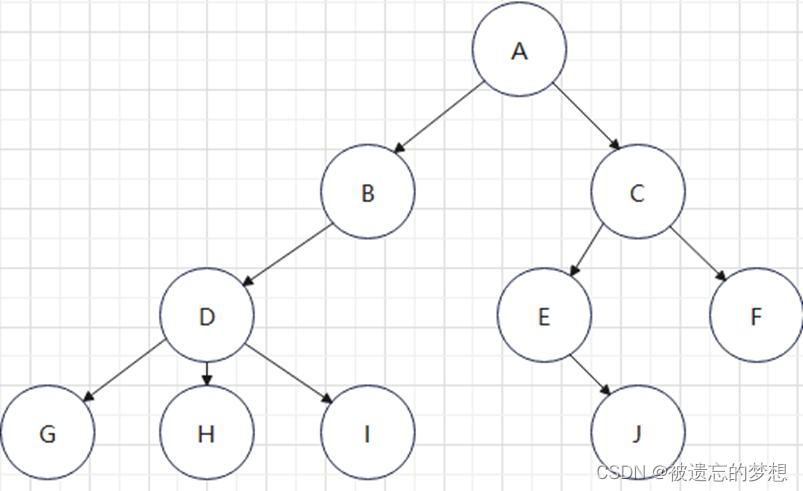
结点：树的每一个数据，如结点A，结点B……结点J，每一个数据称为结点
结点的度:结点拥有子树的数量例如结点D拥有3个子树分别是GHI，所以结点D的度是3
树的度：树中所有结点度的最大值，如D的度是3，是所有结点的度最大值，树的度是3
叶子结点：度为0，没有后继的结点，如GHIJ都是叶子结点，也称为终端结点
分支结点：不是叶子结点称为分支结点，如BCDE，也就是存在后继的结点
孩子：一个结点的直接后继，如B是A的孩子，C是A的孩子
双亲：一个结点的前驱，如A是B的双亲，A也是C的双亲
堂兄弟：双亲在同一层的结点互为堂兄弟；
兄弟：同一双亲的孩子之间称为兄弟，如B和C是兄弟，他们都是A的孩子，同时A是B结点和C结点的双亲

祖先：从根结点到达该结点所走的路，中途遇到的每一个结点称为该节点祖先，如结点H，我从根结点出发，途中经过BD然后才到达H，所以，H的祖先有ABD

子孙：以某结点为根的所有子树中的任意结点都称为该结点的子孙，例如对于B来说，每一个结点也是一个集合，同时也表示一棵树，如果吧B结点当作树根，那么他的子树有DGHI，所以他的所有子树组成的集合就是该结点的子孙

树的层次：第一层是根结点，第二层是BC，第三层是DEF，第四层是GHIJ
树的深度(高度)：树有几层就是他的最大高度
有序树：树中的结点的各子树看成从左往右是有次序的。
森林：对树中的每一个结点来说，该结点的子树的集合称为森林，如根结点A，他有两个子树分别是BC