二叉树的5种性质、5种分类、如何定义并创建二叉树、4种遍历方式和完整代码

最新推荐文章于 2025-03-16 12:27:29 发布

itmengge

最新推荐文章于 2025-03-16 12:27:29 发布

阅读量3.2k

点赞数 3

分类专栏：数据结构与算法文章标签： java 数据结构算法排序算法

本文链接：https://blog.youkuaiyun.com/qq_49432338/article/details/123262629

版权

数据结构与算法专栏收录该内容

1 篇文章

订阅专栏

二叉树的5种性质、5种分类、如何定义并创建二叉树、4种遍历方式和完整代码

一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根节点加上两棵分别称为左子树和右子树的二叉树组成。

1、二叉树的性质

性质一：在二叉树的第 i 个点上至多有 2*i-1 各基地单个节点。
性质二：深度为 k 的节点上至多有 2*k-1 个节点（k≥1）。
性质三：对任何一棵二叉树T，如果其终端结点数为 n0 ，度为2的结点数为 n2 ，则 n0=n2+1 。
性质四：具有 n 个结点的完全二叉树的深度为 ⌊log2n⌋+1 。
性质五：如果对一棵有n个结点的完全二叉树（其深度为 ⌊log2n⌋+1 ）的结点按层序编号（从第1层到第 ⌊log2n⌋+1 层，每层从左到右），则对任一结点i（1≤i≤n），有：
（1）如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲PARENT(i)是结点 ⌊i/2⌋
（2）如果2*i>n，则结点n无左孩子（结点i为叶子结点）；否则其左孩子LCHILD(i)是结点 2*i
（3）如果2*i+1>n，则结点i无右孩子，否则其右孩子RCHILD(i)是结点 2i+1

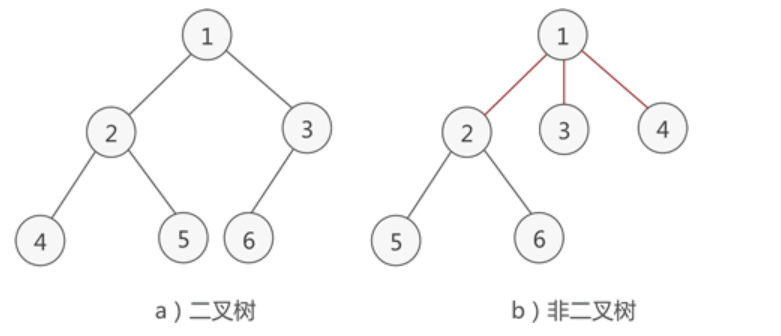
2、二叉树的分类

二叉树

每个结点最多有两棵子树，即二叉树不存在度大于2的结点
二叉树的子树有左右之分，其子树的次序不能颠倒

满二叉树

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点二叉树。
国内教程定义：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。

完全二叉树

完全二叉树是一种特殊的二叉树，满足以下要求：
所有叶子节点都出现在 k 或者 k-1 层，而且从 1 到 k-1 层必须达到最大节点数；
第 k 层可以不是满的，但是第 k 层的所有节点必须集中在最左边。
需要注意的是不要把完全二叉树和“满二叉树”搞混了，完全二叉树不要求所有树都有左右子树，
但它要求：任何一个节点不能只有左子树没有右子树。
叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。

4、二叉查找树/二叉搜索树/二叉排序树

二叉查找树（又叫二叉排序树），它是是一个有序树，具有下列性质的二叉树：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

它的左、右子树也分别为二叉搜索树/二叉排序树。

二叉查找树中，左子树都比节点小，右子树都比节点大，递归定义。

根据二叉排序树这个特点我们可以知道：二叉排序树的中序遍历一定是从小到大的。

这就决定了，二叉搜索树，递归遍历和迭代遍历和普通二叉树都不一样。

平衡二叉树

平衡二叉树的提出就是为了保证树不至于太倾斜，尽量保证两边平衡。因此它的定义如下：
平衡二叉树要么是一棵空树
要么保证左右子树的高度之差不大于 1
子树也必须是一颗平衡二叉树

3、树的遍历

3.1 树的遍历分类

树的遍历分为两类：

深度优先（DFS）
前序遍历
中序遍历
后序遍历

广度优先（BFS）
层次遍历

（1）通过前中序、和中后序确定一个唯一的二叉树

通过前序和中序、或者中序和后序，能够确定一个确定的二叉排序树。
但是前序和后序搭配在一起，是无法确定唯一的二叉树的。

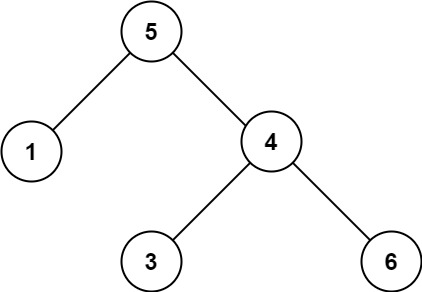
（2）二叉排序树（二叉查找树/二叉搜索树）的中序遍历是有序数组

二叉排序树的中序遍历是有序的，且为升序（参考下面的图）

3.2 定义并创建二叉树

定义二叉树

//定义二叉树
class TreeNode {
	
	String value;     //根节点的值
	TreeNode leftChild;    //左子树
	TreeNode rightChild;    //右子树

	//构造函数
	public TreeNode() {

	}
	public TreeNode(String value) {
		this.value = value;  
	}
	public TreeNode(String value, TreeNode leftChild, TreeNode rightChild) {
		this.value = value;
		this.leftChild = leftChild;
		this.rightChild = rightChild;
	}
	
	
}

创建二叉树

// 创建一个二叉树
public static TreeNode createTree(String[] strs) {

    //创建列表datas用以存储二叉树的所有节点
    List<TreeNode> datas = new ArrayList<>();

    //按循序为每一个数据都添加相应的节点
    for (String str : strs) {
        datas.add(new TreeNode(str));
    }

    // 将第一个节点作为根节点
    TreeNode root = datas.get(0);

    //为每一个节点赋值
    for (int i = 0; i < strs.length / 2; i++) {

        datas.get(i).leftChild = datas.get(i * 2 + 1);    //i位置节点的左子树位置为：i*2+1

        // 避免偶数的时候 下标越界
        if (i * 2 + 2 < datas.size()) {
            datas.get(i).rightChild = datas.get(i * 2 + 2);    //i位置节点的左子树位置为：i*2+2
        }

    }

    //将根节点返回
    return root;

}

//或
//	public static TreeNode createTree() {
//		// 叶子节点
//		TreeNode G = new TreeNode("G");
//		TreeNode D = new TreeNode("D");
//		TreeNode E = new TreeNode("E", G, null);
//		TreeNode B = new TreeNode("B", D, E);
//		TreeNode H = new TreeNode("H");
//		TreeNode I = new TreeNode("I");
//		TreeNode F = new TreeNode("F", H, I);
//		TreeNode C = new TreeNode("C", null, F);
//		// 构造根节点
//		TreeNode root = new TreeNode("A", B, C);
//		return root;
//	}

3.3 深度优先（DFS）

3.3.1 前序遍历

// 前序遍历
public static void preOrder(TreeNode root) {

    if(root == null) {  //当前节点不存在
        return;
    }

    if(root.value!=null) {   //不输出值为null的节点（节点存在，但值可能为null）
        System.out.print(root.value+" ");
    }
    preOrder(root.leftChild);
    preOrder(root.rightChild);

}

3.3.2 中序遍历

// 中序遍历
public static void inOrder(TreeNode root) {

    if(root == null) {  //当前节点不存在
        return;
    }

    inOrder(root.leftChild);
    if(root.value!=null) {    //不输出值为null的节点（节点存在，但值可能为null）
        System.out.print(root.value+" ");
    }
    inOrder(root.rightChild);

}

3.3.3 后序遍历

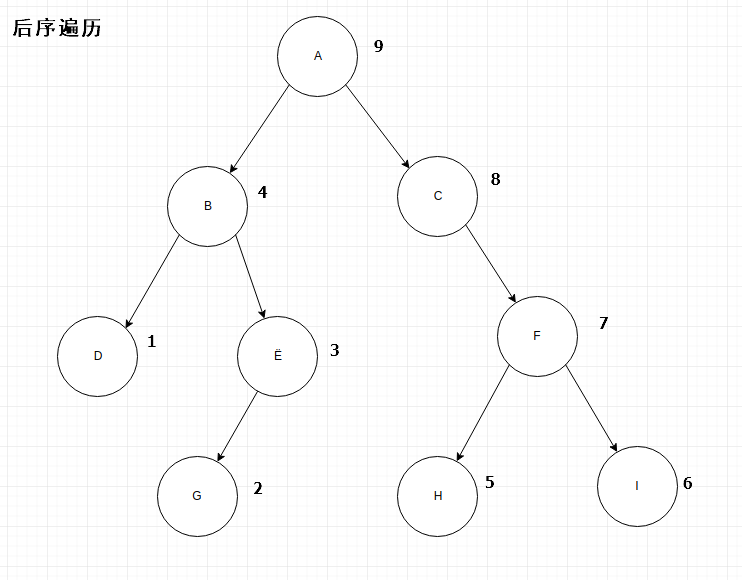
// 后序遍历
public static void postOrder(TreeNode root) {

    if(root == null) {  //当前节点不存在
        return;
    }

    postOrder(root.leftChild);
    postOrder(root.rightChild);
    if(root.value!=null) {      //不输出值为null的节点（节点存在，但值可能为null）
        System.out.print(root.value+" ");
    }

}

3.4 广度优先（层次遍历）（BFS）

//层次遍历
public static void levelOrder(TreeNode root) {

    if(root == null) {  //当前节点不存在
        return;
    }

    //存储所有节点
    LinkedList<TreeNode> nodes=new LinkedList<>();
    nodes.add(root);
    TreeNode node;

    while(nodes.isEmpty()==false) {

        node=nodes.poll();    //获取并移除此列表的头
        if(node.value != null) {      //不输出值为null的节点（节点存在，但值可能为null）
            System.out.print(node.value+" ");
        }

        if(node.leftChild != null) {
            nodes.add(node.leftChild);
        }
        if(node.rightChild != null) {
            nodes.add(node.rightChild);
        }

    }

}

4、完整代码

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

public class Main {
	
	public static void main(String[] args) {
		
		// 二叉树的顺序节点
		String[] strs={"A","B","C","D","E",null,"F",null,null,"G",null,null,null,"H","I"};

		// 构造根节点
		TreeNode root=new TreeNode();
//		
		// 创建一个二叉树
		root=createTree(strs);
		
		TreeNode tree=new TreeNode();
		
		System.out.print("前序遍历:");   
		preOrder(root);   //前序遍历:A B D E G C F H I 
		System.out.println();
		
		System.out.print("中序遍历:");   
		inOrder(root);    //中序遍历:D B G E A C H F I 
		System.out.println();
		
		System.out.print("后序遍历:");   
		postOrder(root);  //后序遍历:D G E B H I F C A 
		System.out.println();
		
		System.out.print("循序遍历:");  //循序遍历:A B C D E F G H I 
		levelOrder(root);
		
		
	}
	
	
	// 创建一个二叉树
	public static TreeNode createTree(String[] strs) {
		
		//创建列表datas用以存储二叉树的所有节点
		List<TreeNode> datas = new ArrayList<>();
		
		//按循序为每一个数据都添加相应的节点
		for (String str : strs) {
			datas.add(new TreeNode(str));
		}
		
		// 将第一个节点作为根节点
		TreeNode root = datas.get(0);
		
		//为每一个节点赋值
		for (int i = 0; i < strs.length / 2; i++) {
			
			datas.get(i).leftChild = datas.get(i * 2 + 1);    //i位置节点的左子树位置为：i*2+1
			
			// 避免偶数的时候 下标越界
			if (i * 2 + 2 < datas.size()) {
				datas.get(i).rightChild = datas.get(i * 2 + 2);    //i位置节点的左子树位置为：i*2+2
			}
			
		}
		
		//将根节点返回
		return root;
		
	}
	
	//或
	//	public static TreeNode createTree() {
	//		// 叶子节点
	//		TreeNode G = new TreeNode("G");
	//		TreeNode D = new TreeNode("D");
	//		TreeNode E = new TreeNode("E", G, null);
	//		TreeNode B = new TreeNode("B", D, E);
	//		TreeNode H = new TreeNode("H");
	//		TreeNode I = new TreeNode("I");
	//		TreeNode F = new TreeNode("F", H, I);
	//		TreeNode C = new TreeNode("C", null, F);
	//		// 构造根节点
	//		TreeNode root = new TreeNode("A", B, C);
	//		return root;
	//	}

	
	// 前序遍历
	public static void preOrder(TreeNode root) {

		if(root == null) {  //当前节点不存在
			return;
		}
	
		if(root.value!=null) {   //不输出值为null的节点（节点存在，但值可能为null）
			System.out.print(root.value+" ");
		}
		preOrder(root.leftChild);
		preOrder(root.rightChild);

	}

	// 中序遍历
	public static void inOrder(TreeNode root) {

		if(root == null) {  //当前节点不存在
			return;
		}
		
		inOrder(root.leftChild);
		if(root.value!=null) {    //不输出值为null的节点（节点存在，但值可能为null）
			System.out.print(root.value+" ");
		}
		inOrder(root.rightChild);

	}
 
	// 后序遍历
	public static void postOrder(TreeNode root) {

		if(root == null) {  //当前节点不存在
			return;
		}
		
		postOrder(root.leftChild);
		postOrder(root.rightChild);
		if(root.value!=null) {      //不输出值为null的节点（节点存在，但值可能为null）
			System.out.print(root.value+" ");
		}

	}
	
	//层次遍历
	public static void levelOrder(TreeNode root) {
		
		if(root == null) {  //当前节点不存在
			return;
		}
			
		//存储所有节点
		LinkedList<TreeNode> nodes=new LinkedList<>();
		nodes.add(root);
		TreeNode node;
		
		while(nodes.isEmpty()==false) {
			
			node=nodes.poll();    //获取并移除此列表的头
			if(node.value != null) {      //不输出值为null的节点（节点存在，但值可能为null）
				System.out.print(node.value+" ");
			}
			
			if(node.leftChild != null) {
				nodes.add(node.leftChild);
			}
			if(node.rightChild != null) {
				nodes.add(node.rightChild);
			}
			
		}
		
	}
	

}


//定义二叉树
class TreeNode {
	
	String value;   //根节点的值
	TreeNode leftChild;    //左子树
	TreeNode rightChild;    //右子树

	
	//构造函数
	public TreeNode() {

	}
	public TreeNode(String value) {
		this.value = value;  
	}
	public TreeNode(String value, TreeNode leftChild, TreeNode rightChild) {
		this.value = value;
		this.leftChild = leftChild;
		this.rightChild = rightChild;
	}
	
	
}