球谐函数（环境光照）

原创

已于 2022-10-04 15:20:12 修改 · 1.5k 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#图形渲染 #游戏引擎 #ue4 #虚幻 #unity

于 2022-10-03 15:01:48 首次发布

球谐函数，源自物理学，用于分解球面上的函数，类似傅里叶变换。在游戏开发和图形渲染中，它被用于环境光的参数化，通过有限数量的球谐系数来近似表示低频光照。这种表示方式具有标准正交性和旋转不变性，当环境光或模型旋转时，仅需对球谐系数进行矩阵变换即可。通常，3到5阶的球谐系数足以应对大多数场景。

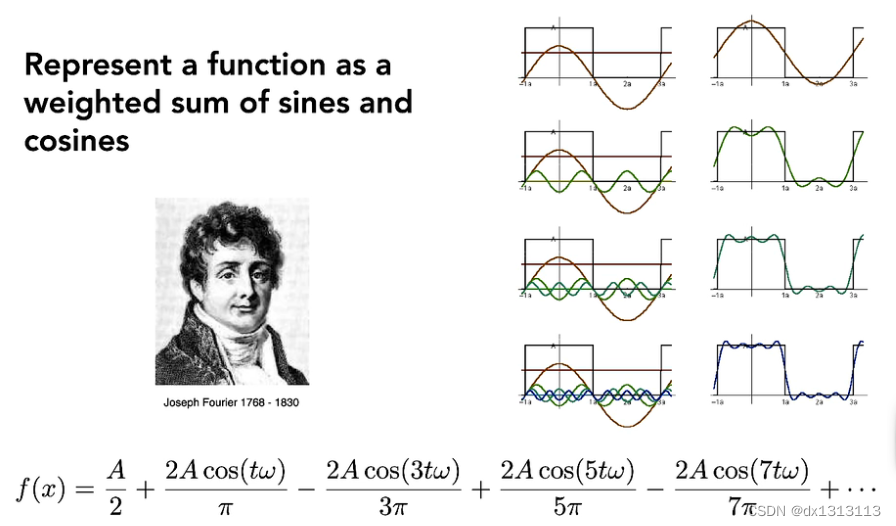
球谐函数（spherical harmonics）本身是来自物理学的一个概念，是对定义在球面上的函数的分解，类似于傅里叶变换是对一维函数的分解一样。傅里叶变换将一维函数分解为不同频率的正弦函数的累加，而球谐函数将球面上的函数分解为一组（无穷多个）标准正交的基底的累加，适用于直接分析球面上一些函数的性质。

傅里叶变换分解

类比傅里叶变换，球谐函数是将球面上的函数分解为一组基函数的累加：

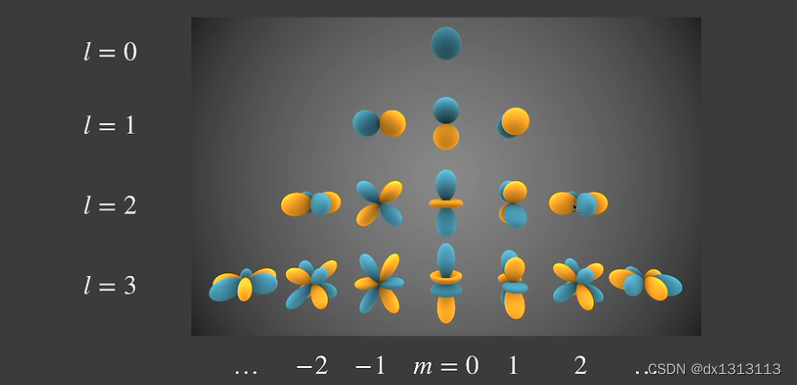
基函数如下图所示（黄色为负，蓝色为正，具有旋转不变性：每一组的某一个可以由同一组的其他的基函数线性组合表示）

其中的每一个基函数都是由勒让德多项式得到（我们不需要了解，太复杂）

那为什么会突然提到球谐函数呢？因为环境光表示的是三维空间中各个方向上的光线，刚好可以看做是定义在球面上的函数，有了这一层“关系”，我们就可以利用球谐函数，将环境光参数化，既方便存储也方便使用。参数化的时候会有一个近似，因为如果完整地表示环境光，需要无穷多个球谐参数。这很明显是不可能的。好在绝大部分参数表示的都是高频光照，作用不是很大，可以忽略掉。对于常用的低频光照，3 ~ 5阶（9 ~ 25个)球谐系数就足够了。

球谐函数有很多优良特性<