计算机基础知识：信息的表示与进制转换-优快云博客

本文详细介绍了计算机中信息表示的基础知识，包括数制的概念、进位计数制的要素（基数、数位、位权和按权展开表达式），以及不同进制之间的转换方法。特别强调了二进制的重要性，如计算机采用二进制的原因、二进制运算（加法、减法、乘法和除法）以及逻辑运算。还涵盖了数值型数据在计算机中的表示，如真值、机器数（定点数和浮点数）、原码、反码和补码的概念，以及非数值型数据的编码，如BCD码、ASCII字符编码和中文字符编码（GB2312）。

一、数制的概念

二、进位计数制

计算机的主要功能是进行数值运算、信息处理和信息存储。

在计算机中对表示数值、文字、声音、图形、图像等各类信息的数据所进行的运算、处理与存储，是由复杂的数字逻辑电路完成的。数字逻辑电路只能接收、处理二进制数据代码，因此，计算机中数值和信息的表示方法，存储方式与我们日常使用的方法是不同的。

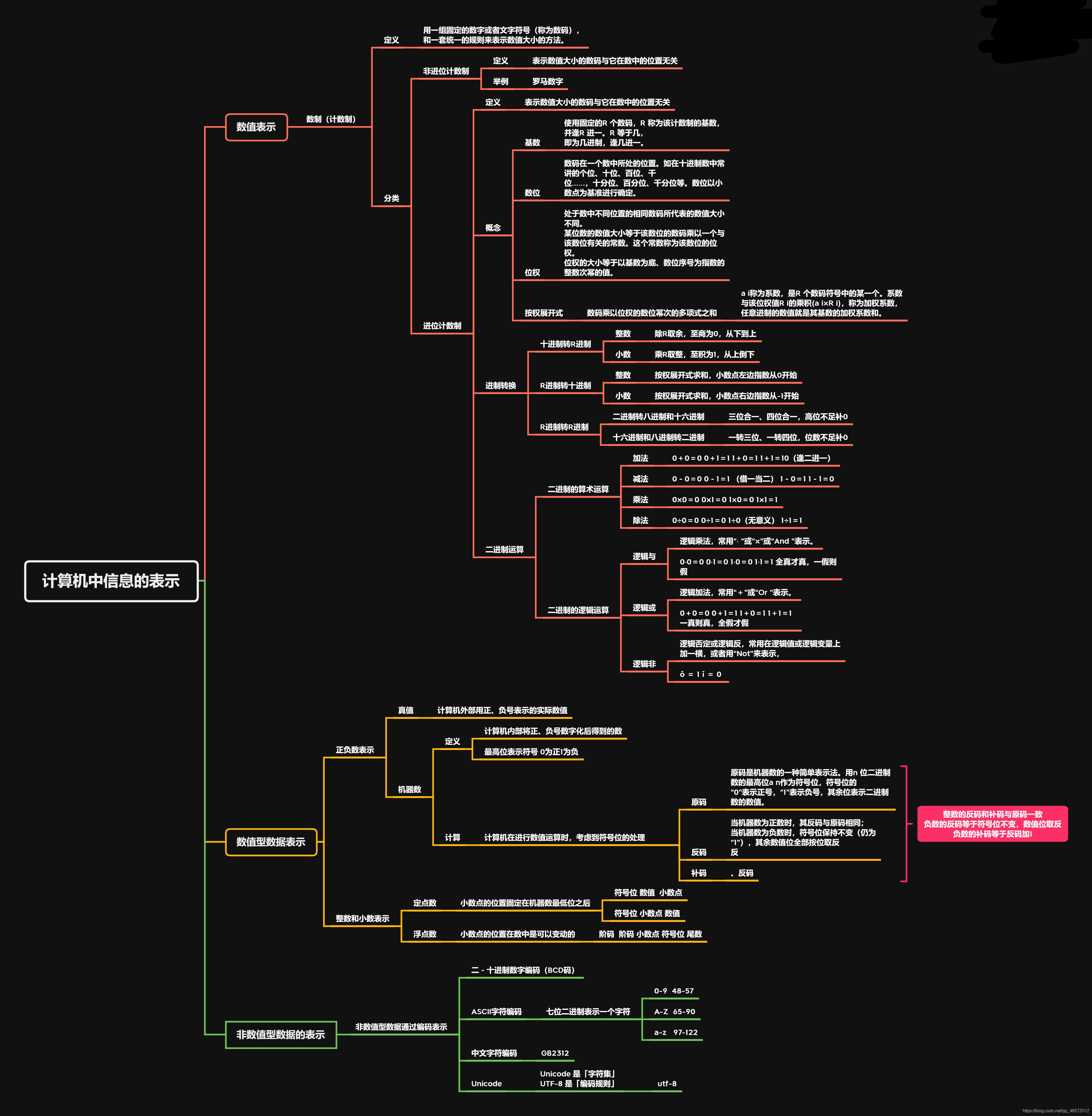
一、数制的概念

数制又称为计数制，

用一组固定的数字或者文字符号（称为数码），和一套统一的规则来表示数值大小的方法。

根据计数规则和特点的不同，数制可以分为非进位计数制和进位计数制两类。

1.非进位制：表示数值大小的数码与它在数中的位置无关的计数体制称之为非进位计数制。

罗马数字就是一种非进位计数制。

最常见的罗马数字(1-12)：Ⅰ-1、Ⅱ-2、Ⅲ-3、Ⅳ-4、Ⅴ-5、Ⅵ-6、Ⅶ-7、Ⅷ-8、Ⅸ-9、Ⅹ-10、Ⅺ－11、Ⅻ－12

罗马数字：XIII－13、XIV－14、XV－15、XVI－16、XVII－17、XVIII－18、XIX－19、XX－20、XXI－21、XXII－22、XXIX－29、XXX－30、XXXIV－34、XXXV－35、XXXIX－39、XL－40、L－50、LI－51、LV－55、LX－60、LXV－65、LXXX－80、XC－90、XCIII－93、XCV－95、XCVIII－98、XCIX－99

2.进位制：表示数值大小的数码与它在数中的位置有关，采用进位原则的计数体制称为进位计数制。

我们日常生活中使用的通常都是进位计数制，常见的一些进位计数制有：
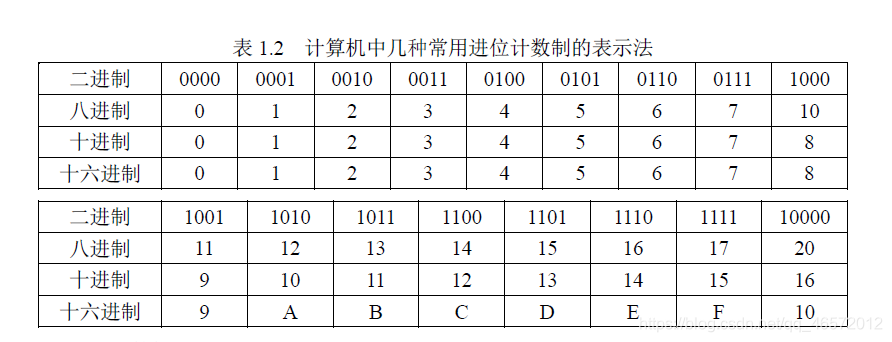
① 十进制(Decimal)：十个数码，0，1，2，3，4，5，6，7，8，9。逢十进一。
②二进制(Binary)：两个数码：0，1。逢二进一。
③八进制(Octal): 八个数码：0，1，2，3，4，5，6，7。逢八进一。通常以0开头
④十六进制(Hexadecimal):十六个数码：0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F。逢十六进一。通常以0X开头。
⑤ 六十进制：计量时间的时、分、秒；计量角度的度、分、秒，均为逢六十进一。
⑥ 二十四进制：计量时间的每日二十四小时，逢二十四进一。
⑦十二进制：计量时间的年、月；十二小时计时制；英制计量单位，均为逢十二进一。

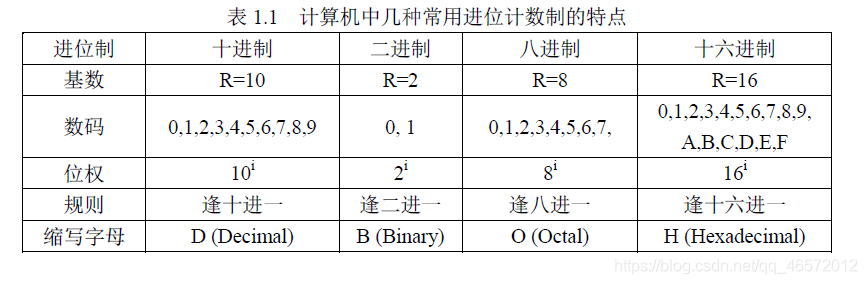
二、进位计数制

各种进位计数制都具有一些共同特点：使用了固定数量的若干个数码；在一个数中，同
一个数码处在不同的位置上表示的数值的大小不同。因此，可以得到构成进位计数制的三个
要素，它们是：

1. 基数

进位计数制使用固定的R 个数码，R 称为该计数制的基数，并逢R 进一。R 等于几，
即为几进制，逢几进一。
例如十进制数，有十个数码：0、1、2、3、4、5、6、7、8、9，基数为十，逢十进一；
二进制数，只有0和1 两个数码，基数为二，逢二进一。

2.数位

数位指的是数码在一个数中所处的位置。如在十进制数中常讲的个位、十位、百位、千
位……，十分位、百分位、千分位等。数位以小数点为基准进行确定。

3. 位权

在进位计数制中，处于数中不同位置的相同数码所代表的数值大小不同。某位数的数值
大小等于该数位的数码乘以一个与该数位有关的常数。这个常数称为该数位的位权。
位权的大小等于以基数为底、数位序号为指数的整数次幂的值。

4.按权展开表达式

十进制数666.66 表示为
(666.66) 10 ＝ 6×10 2＋6×10 1＋6×10 0＋6×10 -1＋6×10 -2
＝ 6×100＋6×10＋6×1＋6×0.1＋6×0.01
＝ 600＋60＋6＋0.6＋0.06
由上式可以看出，位权值的大小等于基数的某次幂，而幂的值取决于数位。因此，各种进位计数制所表示的数值都可以写成按其位权展开的多项式之和。

对任意一个R进制数M可表示为：

其中的a i称为系数，是R 个数码符号中的某一个。系数与该位权值R i的乘积(a i×R i)
称为加权系数，任意进制的数值就是其基数的加权系数和。

三、进制转换

不同进位计数制之间的转换，其实质是基数间的转换。任何有理数都可以写成某种进位
计数制的按权展开表达式。如果两个有理数相等，则这两个数的整数部分和小数部分一定分
别相等。根据这个转换原则，在不同数制间进行转换时，通常对整数部分和小数部分分别进
行转换。

1.十进制转R进制

将十进制数转换成R进制数时，需要对整数部分和小数部分分别进行，然后将各自得到
的结果组合，以获得最后结果。转换步骤如下：

① 整数的转换：采用除R取余法，得到的余数，其高低位顺序由后(下)向前(上)取；
② 小数的转换：采用乘R取整法，得到的整数，其高低位顺序由前(上)向后(下)取；
③ 将转换获得的整数和小数部分组合起来，即得转换后的R进制数。

示例：

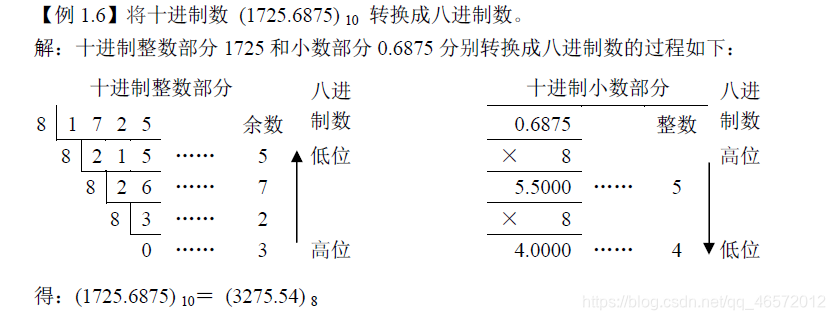
2.R进制转十进制

写出以该进制数的基数为底的按权展开式，乘幂求和算出该多项式的结果即可。

3.R进制转R进制

①以十进制为中介转换

先将R进制转换为十进制，在将转换后的十进制转换为R进制

②按位转换

二进制<=>R进制

因为八进制的基数为8，十六进制的基数为16，分别为二进制的基数2 的3 次方和4
次方，即1 位八进制数可以用3 位二进制数表示，1 位十六进制数可以用4位二进制数表示。
因此二进制数与八进制数、十六进制数之间的相互转换直接而又简便。

① 二进制数转换成八进制数
将二进制数转换成八进制数的方法是：以小数点为界，整数部分向左，小数部分向右，
每三位一组，用相应的八进制数表示，到左端最高位或右端最低位不足三位时，用0 补足。
② 二进制数转换成十六进制数
将二进制数转换成十六进制数的方法是：以小数点为界，整数部分向左，小数部分向右，
每四位一组，用相应的十六进制数表示，到左端最高位或右端最低位不足四位时，用0 补足。

R进制<=>二进制

将八进制数、十六进制数转换成二进制数的方法是上述转换方法的逆操作。只要将每位
八进制数或十六进制数分别用相应的三位或四位二进制数表示即可。

八进制<=>十六进制

先转化为二进制或十进制再进行转换

四、二进制

1.计算机与二进制

在计算机中采用二进制数表示各种信息数据，进行运算，主要是因为二进制本身具有一
些独特的优点：
① 表示方便
二进制数只有0和1两个数码，在计算机中非常容易用电子元器件、电子线路、磁芯等
物理部件的两种不同的物理状态来表示。如晶体管的导通与截止，电容的充电和放电，开关
的接通与断开，电流的有与无，灯的亮与灭，磁芯磁化极性的不同等两个截然不同的对立状
态都可用于表示二进制数。将多个器件排列起来，就可表示多位二进制数。
如果采用十进制，则需要在硬件上实现十个稳定的物理状态，来表示从0～9的10个数
码，这是非常困难的。
② 运算简单
二进制的运算法则比较简单，如二进制的加法运算法则只有四条：
0＋0＝0 0＋1＝1 1＋0＝1 1＋1＝10（逢二进一）
而十进制的加法运算法则有100条。另外，二进制数的乘、除法运算只需要通过加法运
算和移位操作就可以完成，这比十进制数的乘、除法运算要简便得多，据此设计的计算机运
算器硬件结构大为简化，也为计算机软件的设计带来很大方便。
③ 逻辑运算
逻辑代数又称布尔代数，是计算机逻辑电路设计的重要理论工具和二值逻辑运算的理论
基础。二进制的两个数码0和1正好与逻辑代数中的真（True）和假（False）相对应，所以
采用二进制，既便于使用逻辑代数的方法去设计和简化计算机的各种逻辑电路，也可以在计
算机中根据二值逻辑进行逻辑运算。
④ 可靠性高
二进制数只有0和1两个基本数码，在存储、传输和处理时不容易出错，可靠性高。
⑤ 转换方便
计算机使用二进制，人们习惯于使用十进制。而二进制与十进制间的转换很方便，二进
制与八进制、十六进制的转换也很简单，因此使人与计算机间的信息交流既简便又容易。

2.二进制的运算

二进制数的运算包括通常的算术运算和特有的逻辑运算两类。

（1）算术运算

二进制数的算术运算与十进制算术运算类似，包括加法、减法、乘法和除法四种运算。
基本运算是加法和减法运算。

①加法运算

0＋0＝0 0＋1＝1 1＋0＝1 1＋1＝10（逢二进一）

② 减法运算

0－0＝0 0－1＝1 （借一当二） 1－0＝1 1－1＝0

③ 乘法运算

0×0＝0 0×1＝0 1×0＝0 1×1＝1

【例1.10】求(10101.11) 2 × (11.01) 2 ＝？

④ 除法运算

0÷0＝0 0÷1＝0 1÷0（无意义） 1÷1＝1

【例1.11】求(101110.01) 2 ÷ (101) 2 ＝？

（2）逻辑运算

如果把二进制数码“0”和“1”表示成“真”和“假”、“是”和“非”、“有”和“无”
等相对立的两种变量值，这种变量称为逻辑变量。描述逻辑变量关系的函数称为逻辑函数。
实现逻辑函数的电路称为逻辑电路。实现逻辑变量之间的运算称为逻辑运算。逻辑运算是逻
辑代数的研究内容。
逻辑运算是一种研究因果关系的运算，在计算机中其运算结果不表示数值的大小，而是
表示一种二元逻辑值：真（True）或假（False）。二进制的逻辑运算与算术运算的主要区别
是：逻辑运算是按位进行的，各位之间互相独立，位与位之间不存在进位和借位的关系。
基本逻辑运算有三个：逻辑与运算（逻辑乘）、逻辑或运算（逻辑加）、逻辑非运算（逻
辑否定）。此外，还有由三种基本逻辑运算组合构成的一些复合逻辑运算，如异或运算、同
或运算、与非运算、或非运算、与或非运算、或与非运算等。在这里只介绍三种基本逻辑运
算。
⑴

①逻辑与

又称逻辑乘法，常用“· ”或“×”或“And ”表示。

0·0＝0 0·1＝0 1·0＝0 1·1＝1 全真才真，一假则假

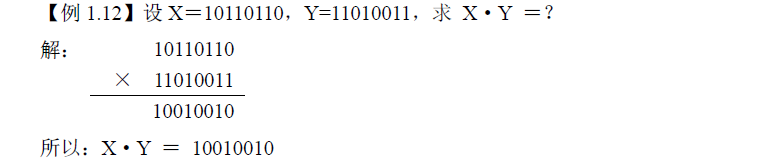
②逻辑或

逻辑加法，常用“＋”或“Or ”表示。

0＋0＝0 0＋1＝1 1＋0＝1 1＋1＝1 一真则真，全假才假

③逻辑非

又称逻辑否定或逻辑反，常用在逻辑值或逻辑变量上加一横，或者用“Not”来表示，

ō ＝ 1 ī ＝ 0

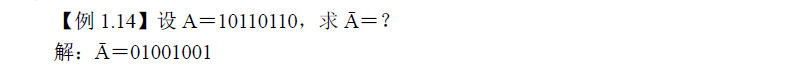
五、数值型数据在计算机中的表示

1．真值与机器数

将计算机使用的二进制数的最高位作为符号位，用“0”表示正号，“1”表示负号。用其余位表示数值的大小。这种在计算机内部将正、负号数字化后得到的数称为机器数，而在计算机外部用正、负号表示的实际数值，称为该机器数所表示的真值。

例如：机器数1101 所表示的真值是－5，而不是13。
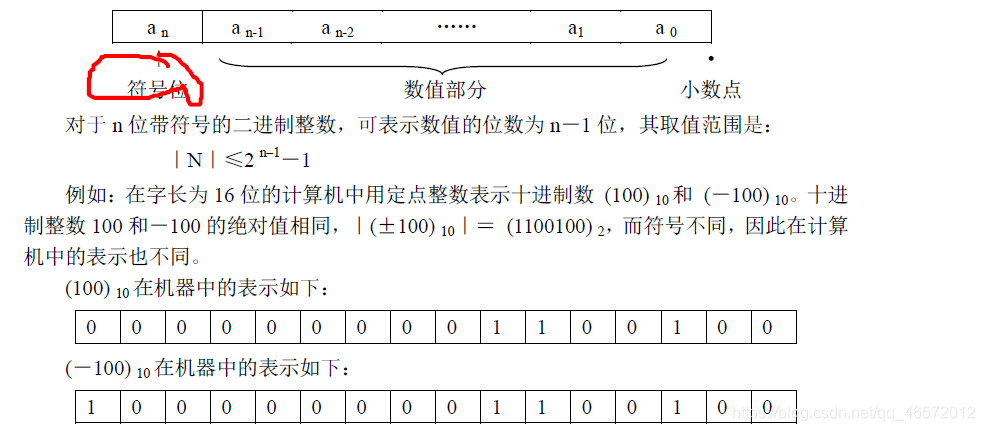
机器数表示的数值范围受到字长和数据类型的限制。计算机的字长和数据类型确定后，
机器数能够表示的数值范围也就确定了。例如对字长为8位的计算机，因为最高位作为符号
位，所以八位二进制机器数在计算机中所能表示的最大值是(01111111) 2，对应十进制数为
＋127；最小值为(11111111) 2，对应十进制数为－127，超出这个取值范围的称为溢出。

2．定点数与浮点数

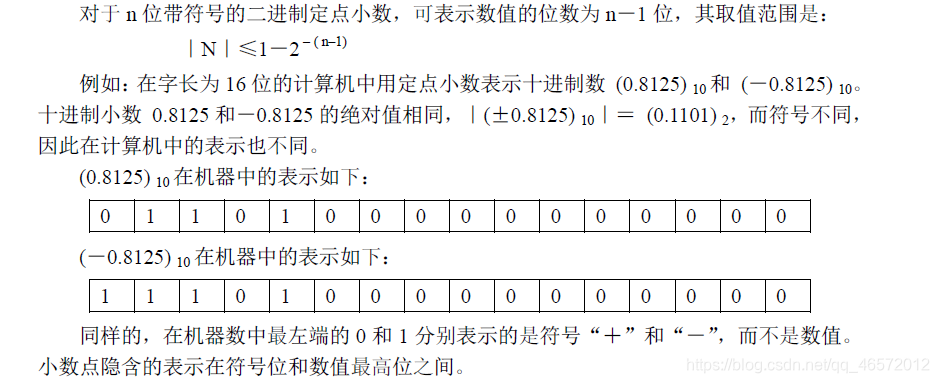
数值不仅有正、负之分，还有整数、小数之分。在计算机中小数点并不占用二进制位，
但是规定了小数点的位置。根据对小数点位置的规定，机器数有整数、定点小数和浮点小数
之分。整数和定点小数都是定点数。

⑴ 定点数

在机器数中，小数点的位置固定不变分为定点定点整数和定点小数

1、定点小数(纯小数)：小数点隐含固定在最高数据位的左边，所以整数位就是最高位用来表示符号位

计算机中存储为 1010111（第一位1为符号位，表示负数）
实际含义：-0.010111
2、定点整数(纯整数)：小数点隐含固定在最低数据位的后边，最高位用来表示符号位

计算机中表示： 10101110
实际含义： -0101110.

(2) 浮点数

小数点的位置在数中是可以变动的。

浮点数将任意二进制数表示成阶码和尾数

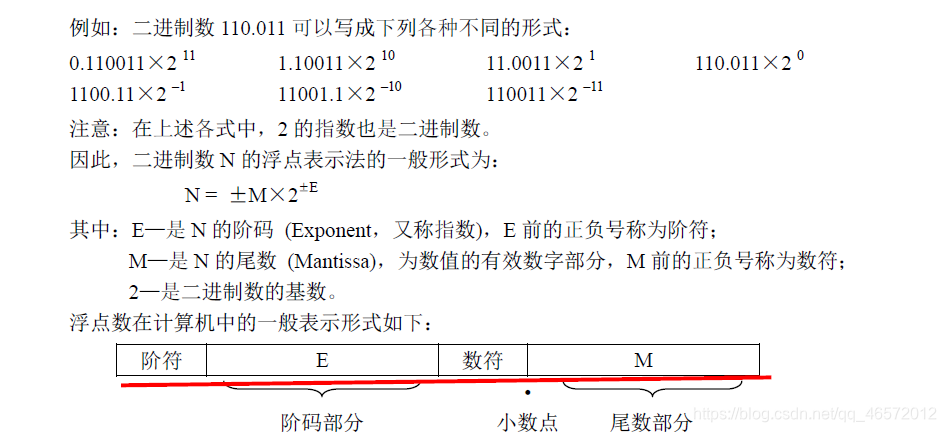由上述表示形式可见，小数点的位置隐含在数符与尾数之间，即尾数总是一个小于 1的数。数符占一位，用于确定该浮点数的正负。阶码总为整数，用于确定小数点浮动的位数。阶符也占一位，用于确定小数点浮动的方向。若阶符为正，小数点向左浮动；若阶符为负，小数点则向右浮动。
为了保证精度，通常需要对浮点小数进行规格化处理，所谓规格化处理指的是要保证尾数部分的最高位为1。

3．原码、反码和补码

从上面对机器数的介绍可以看出，二进制数在计算机中以机器数形式存放时，由符号位
和数值两部分组成，符号和数值全部数字化。符号位占一位，用“0”表示正数，“1”表示
负数，因此，计算机在进行数值运算时，也应考虑到符号位的处理。为了便于计算，机器数
一般有三种表示方法：原码、反码和补码。

⑴ 原码

原码是机器数的一种简单表示法。用n 位二进制数的最高位a n作为符号位，符号位的
“0”表示正号，“1”表示负号，其余位表示二进制数的数值。

设有一个数N 的绝对值是｜N｜＝a n-1 a n-2 …a 1 a 0，则数N的机器数的原码可表示为：

因为在原码中，最高位是符号位，从次高位开始的其余位才是有效数值位，所以n位原码能够表示的数值范围是：。

如字长8位的原码能够表示的整数范围是：

⑵ 反码

机器数的反码表示可以很容易地从原码得到。当机器数为正数时，其反码与原码相同；
当机器数为负数时，符号位保持不变（仍为“1”），其余数值位全部按位取反，得到的就是
反码。

⑶ 补码

机器数的补码表示也同样可以通过原码得到。当机器数为正数时，其补码与原码相同；
当机器数为负数时，符号位保持不变（仍为“1”），其余数值位全部按位取反后再加1，得
到的就是补码。简单地说，负数的补码就等于该数的反码加1。

使用补码表示法的优点是：不仅可以使符号位和有效数值位同时参与数值运算，而且还
可以使减法运算转换成加法运算，从而简化计算机运算器的电路设计。所以，在计算机中，
带符号的数一般都用补码表示。

由上述4个例子可以看出，补码的减法运算实际上是通过对减数求补的方法把减法运算
转换成了加法运算，得到的计算结果也都是正确的。在(3)和(4)两个例子中，与补码加法运
算中一样，作为符号位的最高位参加运算后向高位的进位虽然因机器字长的限制而自动丢
失，但同样未影响运算结果的正确性。

六、非数值型数据在计算机中的表示

计算机中的数据可以分为数值数据和非数值型数据两大类。数值数据用于表示数量的多
少，可以参与数值计算。非数值型数据则包括英文字母、阿拉伯数字、各种标点符号、专用
符号、汉字符，以及表示声音、图形、图像等音频、视频信息的数据。所有这些数据，在计
算机中也都只能采用二进制数的编码形式来表示，所以必须对各种数据进行编码。

所谓编码，指的是使用某种符号的组合，表示特定对象信息的过程。例如邮电部门使用
的电报明码、邮政编码，以及车辆牌号，路牌号码，运动员号码等。

1. 二－十进制数字编码（BCD码）

在日常的工作、生活中人们习惯于使用十进制，但因为二进制的优点，在计算机内部都
使用二进制进行数值运算和信息处理。所以数据在输入计算机前应将十进制转换成二进制，
计算机的运算、处理结果也应转换成十进制再输出。在计算机输入、输出数据，对二进制和
十进制进行转换时，常使用二－十进制编码。
所谓二－十进制编码（Binary Coded Decimal 简称BCD 码）指的是将每一位十进制数
用四位二进制数来表示。因为4位二进制数共有十六种状态组合，取其中的十种状态组合即
可表示十进制数的10 个数码，所以BCD 的编码方案很多。如有8421 码、2421 码、5211 码、余3码、格雷码、余3循环码、右移码等。最常用的是8421码。
8421BCD 码的编码方式最简单，每一位十进制数用四位二进制数表示，自左向右每一
位二进制数对应的位权分别是8、4、2、1，

2. ASCII字符编码

字符数据主要指大小写的英文字母、数字、各种标点符号、控制符号、汉字符等。在计
算机中，它们都被转换成能被计算机识别和接受的二进制编码的形式。除了汉字符，在字符
编码中使用最多、最普遍的是ASCII 字符编码。其全称是American Standard Code for
Information Interchange（美国信息交换标准代码）。ASCII 码现在已经成为西文字符编码的
国际通用标准。
标准ASCII码用7位二进制数表示一个字符。因为27＝128，所以可以表示128 个不同
的字符。在这128 个字符中有95 个编码，对应着使用计算机终端设备（如标准键盘）能够
输入并且可以显示，也可以在打印机上打印出来的95 个字符。

0-9 48-57

A-Z 65-90

a-z 97-122

3．中文字符编码 GB2312

英文和其它西文都是拼音文字，其基本符号比较少，编码较为容易，如上面介绍的ASCII
代码，仅用了一个字节中的低7位即可表示出来。而且在一个计算机系统中，字符的输入、
内部处理、存储、输出等都可以使用同一代码。
用计算机系统处理中文字符，同样需要将中文字符代码化。但由于汉字是一种象形表意
文字，字的数量巨大，不可能像英文那样使用字母拼写出来，也难以用少量的符号表示出来。
而且在一个计算机的汉字处理系统中，中文字符的输入、内部处理、存储和输出等的要求不
尽相同，使用的代码也不尽相同，因此中文字符必须有自己特殊的编码方式。根据汉字在计
算机处理过程中的不同要求，汉字的编码主要分为四类：汉字交换码、汉字机内码、汉字输
入码和汉字字形码。
⑴ 汉字交换码
汉字交换码又简称国标码（GB）。它是由国家制定的用于汉字信息交换的标准汉字编码。
1980 年国家标准局公布了GB2312-80 标准，其全称是“信息交换用汉字编码字符集—基本
集”。该基本集中包含了一、二级汉字6763 个，其它各种字母、标点、图形符号682个，共
计7445 个字符。其中一级汉字3755 个，按拼音字母顺序排序；二级汉字3008 个，按部首
顺序排序

交换码规定：每个汉字符采用两个字节表示，故称之为双字节字符。为了与ASCII 码
兼容，交换码只使用了两个字节的低7 位，各字节的最高位也为0。前一个字节称为区码，
后一个字节称为位码。

GB2312 是简体中文的码

4. Unicode编码

英语用 128 个字符来编码完全是足够的，但是用来表示其他语言，128 个字符是远远不够的。于是，一些欧洲的国家就决定，将 ASCII 码中闲置的最高位利用起来，这样一来就能表示 256 个字符。但是，这里又有了一个问题，那就是不同的国家的字符集可能不同，就算它们都能用 256 个字符表示全，但是同一个码点（也就是 8 位二进制数）表示的字符可能可能不同。例如，144 在阿拉伯人的 ASCII 码中是 گ，而在俄罗斯的 ASCII 码中是 ђ。

因此，ASCII 码的问题在于尽管所有人都在 0 - 127 号字符上达成了一致，但对于 128 - 255 号字符上却有很多种不同的解释。与此同时，亚洲语言有更多的字符需要被存储，一个字节已经不够用了。于是，人们开始使用两个字节来存储字符。

各种各样的编码方式成了系统开发者的噩梦，因为他们想把软件卖到国外。于是，他们提出了一个“内码表”的概念，可以切换到相应语言的一个内码表，这样才能显示相应语言的字母。在这种情况下，如果使用多语种，那么就需要频繁的在内码表内进行切换。

Unicode
最终，美国人意识到他们应该提出一种标准方案来展示世界上所有语言中的所有字符，出于这个目的，Unicode诞生了。

Unicode 当然是一本很厚的字典，记录着世界上所有字符对应的一个数字。具体是怎样的对应关系，又或者说是如何进行划分的，就不是我们考虑的问题了，我们只用知道 Unicode 给所有的字符指定了一个数字用来表示该字符。

对于 Unicode 有一些误解，它仅仅只是一个字符集，规定了符合对应的二进制代码，至于这个二进制代码如何存储则没有任何规定。它的想法很简单，就是为每个字符规定一个用来表示该字符的数字，仅此而已。

Unicode 编码方案
之前提到，Unicode 没有规定字符对应的二进制码如何存储。以汉字“汉”为例，它的 Unicode 码点是 0x6c49，对应的二进制数是 110110001001001，二进制数有 15 位，这也就说明了它至少需要 2 个字节来表示。可以想象，在 Unicode 字典中往后的字符可能就需要 3 个字节或者 4 个字节，甚至更多字节来表示了。

这就导致了一些问题，计算机怎么知道你这个 2 个字节表示的是一个字符，而不是分别表示两个字符呢？这里我们可能会想到，那就取个最大的，假如 Unicode 中最大的字符用 4 字节就可以表示了，那么我们就将所有的字符都用 4 个字节来表示，不够的就往前面补 0。这样确实可以解决编码问题，但是却造成了空间的极大浪费，如果是一个英文文档，那文件大小就大出了 3 倍，这显然是无法接受的。

于是，为了较好的解决 Unicode 的编码问题， UTF-8 和 UTF-16 两种当前比较流行的编码方式诞生了。当然还有一个 UTF-32 的编码方式，也就是上述那种定长编码，字符统一使用 4 个字节，虽然看似方便，但是却不如另外两种编码方式使用广泛。

UTF-8
UTF-8 是一个非常惊艳的编码方式，漂亮的实现了对 ASCII 码的向后兼容，以保证 Unicode 可以被大众接受。

UTF-8 是目前互联网上使用最广泛的一种 Unicode 编码方式，它的最大特点就是可变长。它可以使用 1 - 4 个字节表示一个字符，根据字符的不同变换长度。编码规则如下：

对于单个字节的字符，第一位设为 0，后面的 7 位对应这个字符的 Unicode 码点。因此，对于英文中的 0 - 127 号字符，与 ASCII 码完全相同。这意味着 ASCII 码那个年代的文档用 UTF-8 编码打开完全没有问题。

对于需要使用 N 个字节来表示的字符（N > 1），第一个字节的前 N 位都设为 1，第 N + 1 位设为0，剩余的 N - 1 个字节的前两位都设位 10，剩下的二进制位则使用这个字符的 Unicode 码点来填充。