1.JS排序算法之冒泡排序

冒泡排序（Bubble Sort），顾名思义类似于水中冒泡,较大的数沉下去,较小的数慢慢冒起来。通过交换元素位置，达到排序目的，是一种交换排序。

目录

一、冒泡算法原理

二、冒泡算法分析

三、冒泡算法应用实例

四、冒泡排序适用场景

---

一、冒泡排序算法原理

1.思路

冒泡排序的实现思路是比较任意两个相邻的项, 如果前者比后者大, 则将它们互换位置.

2.流程描述：（以非递减为例）

从第一个元素开始比较相邻的元素。如果第一个比第二个大，就交换他们两个。交换后的第二个元素与第三个元素比较，以此类推直到比较到最后一个元素（实际是倒数第二个元素），称为一趟排序。
n个元素的冒泡排序趟数最多为n-1
每一趟排序都可以得到该趟最大的元素

3.举例：

例：35, 33, 42, 10, 14, 19, 27, 44,

第一趟排序：33,35,10,14,19,27,42

第二趟排序：33,10,14,19,27,35,42

第三趟排序:  10,14,19,27,33,35,42

第四趟排序:  10,14,19,27,33,35,42

······

4.动画演示：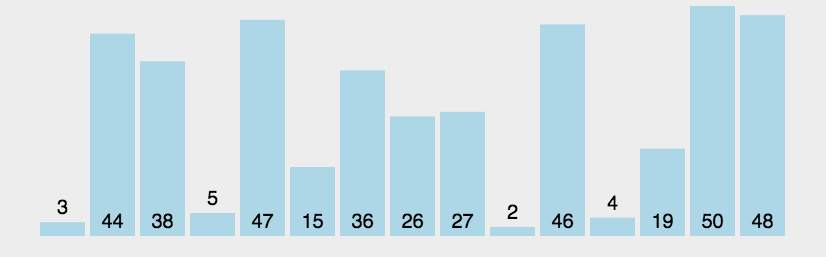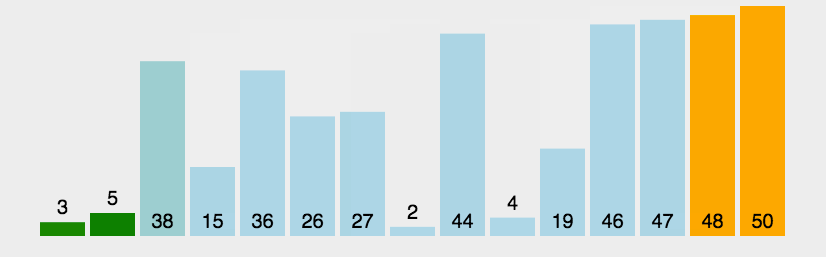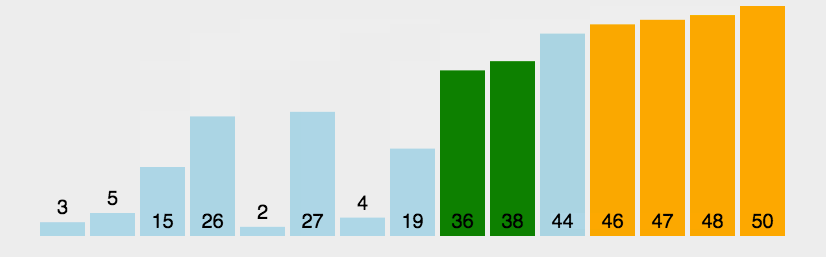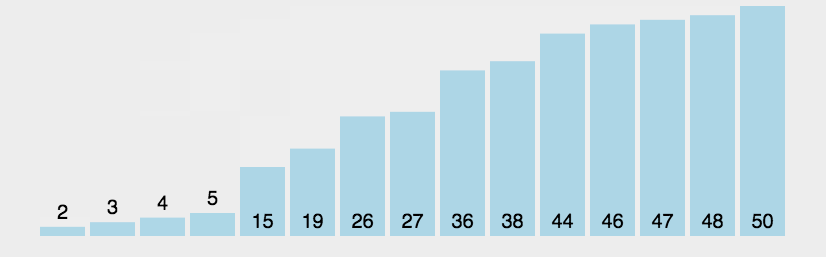

二、冒泡排序算法分析

最好时间复杂度：

O(n)   当输入的数据已经是正序时，比较次数为n-1，无数据交换（优化后的冒泡排序）

最坏时间复杂度：

O(n²)  当输入的数据是反序时，比较次数为1+2+3+...+(n-1) = n(n-1) /2

平均时间复杂度

O(n²)  当输入的数据是乱序时，比较趟数(n - 1)(n + 1) / 2 = (n² - 1)/2

空间复杂度

O(1)  原地排序，辅助空间相对于数据量而言是个常数

稳定性

冒泡排序是稳定排序，不会改变数据的大小相对位置

平均时间复杂度计算

平均复杂度就是加权平均期望时间复杂度，这里我们采用"有序度" 和“逆序度” 来分析。
有序度：数组中具有有序关系的元素对的个数。有序元素用数学表达式就是这样：
有序元素对：a[i] <= a[j], 如果 i < j。(找非逆序对)

比如倒序排列的数组，6 5 4 3 2 1 ，有序度就是 0；
有序数组，比如 1 2 3 4 5 6 ，有序度就是 n*(n-1)/2 也就是15，把这种完全有序的数组的有序度叫作满有序度。并且 逆序度 = 满有序对 - 有序对
用之前的 4，5，6，3，2，1举例来看，有序元素对 (4,5)(4,6)(5,6) 有序度是 3。满有序度： n*(n-1)/2=15。冒泡排序包含的两个操作元素，比较和交换。每交换一次，有序度就加1.不管算法怎么改交换次数总是确定的，即为逆序度， n*(n-1)/2–初始有序度。此例中就是 15–3=12，要进行 12 次交换操作。

对于包含 n 个数据的数组进行冒泡排序，平均交换次数是多少呢？最坏情况下，初始状态的有序度是 0，所以要进行 n*(n-1)/2 次交换。最好情况下，初始状态的有序度是 n*(n-1)/2，就不需要进行交换。我们可以取个中间值 n*(n-1)/4，来表示初始有序度既不是很高也不是很低的平均情况。换句话说，平均情况下，需要 n*(n-1)/4 次交换操作，比较操作肯定要比交换操作多，而复杂度的上限是 O(n^2 )，所以平均情况下的时间复杂度就是 O(n^2 )。这个平均时间复杂度推导过程其实并不严格，但是很多时候很实用，毕竟概率论的定量分析太复杂，不太好用。

（感谢@另维吖，原文地址https://blog.youkuaiyun.com/qq_40488936/article/details/105558986?utm_source=app&app_version=4.9.1）

三、冒泡排序算法应用实例

1.简单交换排序

简单交换排序的原理是，用每一个位置的元素，与其他位置元素一一比较，反序则交换，每趟排序得到一个最(小)值。这种排序方法使得每一个元素都经历多次位置的变换，会造成每趟排序对其余关键字的排序没有帮助。

// 以非递减排序
var arr = [9,1,5,8,3,7,4,6,2];
console.log('原数组：'+ arr);// 标记原数组
function simpleExchangeSort(arr) {
    var len = arr.length;
   
    for (var i = 0; i < len; i++) {
        var num = 1;   // 标记交换次数
        for (var j = i+1; j < len; j++) {  
            if (arr[i] > arr[j]) {        
                var temp = arr[j];       
                arr[j] = arr[i];
                arr[i] = temp;
                console.log('第' + (i+1) + '趟排序的第'+(num++)+'次交换：' + arr); // 标记交换
            }
        }
        console.log('第' + (i+1) + '趟排序：' + arr);// 标记趟数
    }
    return arr;
}

simpleExchangeSort(arr);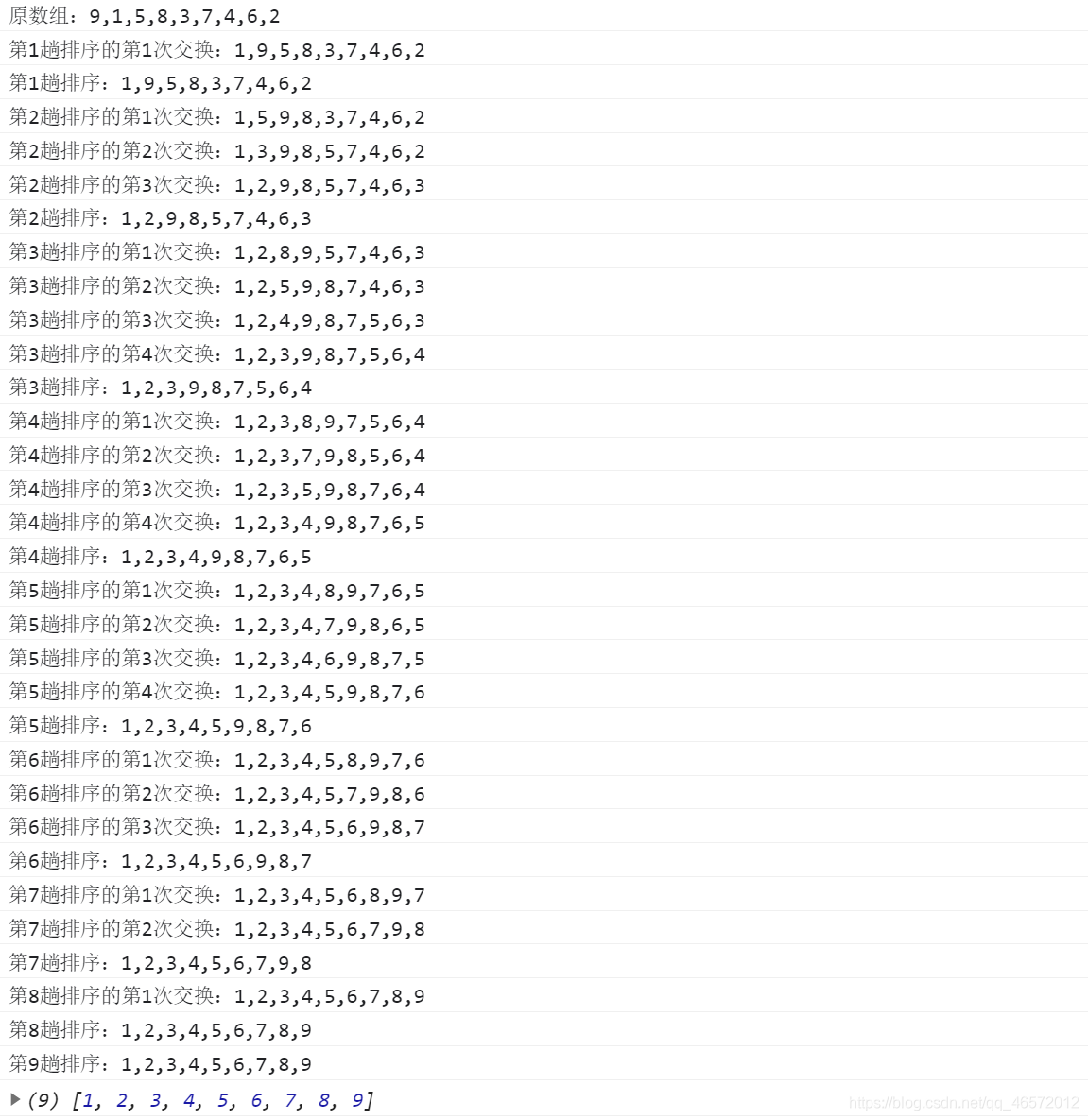

2.冒泡排序

基于简单交换排序，因为每趟排序都可以得到一个确定排序顺序（最大值）的元素，当其余元素都排好了顺序。 最后一个元素自然也就不需要排序，排序趟数的增加，已经排好顺序的数不需要再交换，使得比较交换的次数也在减少。例如5个元素，排序趟数为4趟，每趟比较交换次数从4次依次递减。

var arr = [9,1,5,8,3,7,4,6,2];
console.log('原数组：'+ arr);// 标记原数组
function bubbleSort(arr){
    //外层循环，控制趟数，每一次找到一个最大值
    for (var i = 0; i < arr.length - 1; i++) {
       // 内层循环,控制比较的次数，并且判断两个数的大小
       var num = 1;
       for (var j = 0; j < arr.length - 1 - i; j++) {
          // 如果前面的数大，放到后面(当然是从小到大的冒泡排序)
           if (arr[j] > arr[j+1]) {
                var temp = arr[j+1];
                arr[j+1] = arr[j];
                arr[j] = temp;
                console.log('第' + (i+1) + '趟排序的第'+(num++)+'次交换：' + arr); // 标记交换
            }
       }
       console.log('第' + (i+1) + '趟排序：' + arr);// 标记趟数
    }
    return arr;
}
bubbleSort(arr);

3.冒泡排序再优化

冒泡排序的优化是基于有序数据的情况下不进行无意义的循环，为交换设置标记，无数据交换时说明已有序。

var arr = [3,2,1,4,5,6,7,8,9];
console.log('原数组：'+ arr);// 标记原数组
function bubbleSortBetter(arr){
    //外层循环，控制趟数，每一次找到一个最大值
    for (var i = 0; i < arr.length - 1; i++) {
       // 内层循环,控制比较的次数，并且判断两个数的大小
       var num = 1;
       var flag = true;
       for (var j = 0; j < arr.length - 1 - i; j++) {
          // 如果前面的数大，放到后面(当然是从小到大的冒泡排序)
           if (arr[j] > arr[j+1]) {
                var temp = arr[j+1];
                arr[j+1] = arr[j];
                arr[j] = temp;
                flag = false;
                console.log('第' + (i+1) + '趟排序的第'+(num++)+'次交换：' + arr); // 标记交换
            }

       }
       if(flag){
          break;
       }
       console.log('第' + (i+1) + '趟排序：' + arr);// 标记趟数
    }
    return arr;
}
bubbleSortBetter(arr);

四、冒泡排序算法适用场景

冒泡排序是最简单的一种排序，但时间复杂度较高

只适用于数据规模较小且接近正序的数据。