八、Boosting
- Boosting在分类问题中,通过改变训练样本的权重,学习多个分类器,将这些分类器进行线性组合,提高分类的性能
- 本章主要讨论的问题
- Boosting思路和代表性AdaBoost算法
- 探讨为什么能提高学习精度,从前向分布加法模型解释AdaBoost算法
- 叙述Boosting具体实例——提升树
8.1 AdaBoost算法
8.1.1 Boosting基本思路
- 思想:三个臭皮匠顶过一个诸葛亮的道理,对多个专家的判断进行综合进行判断(提高专家权重,减少普通人的权重)
- 在概率近似框架(PAC)框架中,一个概念可强学习的充要条件是这个概念可弱学习的,换句话说弱学习算法可以提升(boost)为强学习算法
- 强可学习:存在一个多项式学习算法能够学习,且正确率高
- 弱可学习:存在一个多项式学习算法能够学习,但正确率比随机猜测略好
- 对于分类问题而言,Boosting的思路就是从弱学习算法出发得到一系列弱分类器,再组合这些弱分类器(通常是改变概率分布 权值分布)得到强分类器
- 有两个问题需要回答:每一轮如何改变权值/概率分布,如何将弱分类器组合为一个强分类器?AdaBoosting的思路是
- 第一个问题:提高前一个分类器错误分类样本的权值,对应减少分类正确样本的权值,进而让后面的弱分类器更关注于错误分类的样本
- 第二个问题:对于弱分类器的组合,通过加权多数表决法进行,即加大分类误差率小的权值,在表决中起到重大作用,减少分类误差率大的权值。
- 有两个问题需要回答:每一轮如何改变权值/概率分布,如何将弱分类器组合为一个强分类器?AdaBoosting的思路是
8.1.2 AdaBoost算法
【算法8.1 AdaBoost】
- 一开始是假设数据集是均匀分布的
- 接下来就是反复地学习分类器,每一轮顺次地来更新权值
- 这里的分类误差率em是对带有权值的训练数据集进行的分类误差样本求和,在8.2的式子中可以看到到em小于0.5时,αm≥0α_m≥0αm≥0并随着em的减小而增大
- (后面线性组合的时候α的权值,来表示该分类器的性能)。
- 更新训练集权值的时候,分母有一个规范因子,分子是前一个权值乘以根据分类情况进行权值的变化(分类正确是e−αme^{-α_m}e−αm,分类错误是eαme^{α_m}eαm)
- (而更新数据集权值的时候,旨对错误的数据放大权值,所以会这样设计)
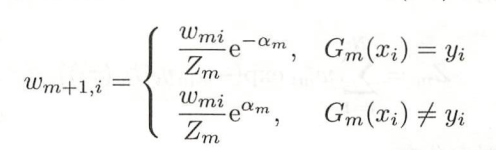
- 经过上述过程后,误分类样本的权值会不断扩大,正确的权值会被缩小,从而实现不改变所给的训练数据,而不断改变数据权值的分布,从而训练数据对于基本分类器的学习有不同的作用(AdaBoost特性1 训练数据在基本分类器中的学习会不断变化权值)
- 这里的分类误差率em是对带有权值的训练数据集进行的分类误差样本求和,在8.2的式子中可以看到到em小于0.5时,αm≥0α_m≥0αm≥0并随着em的减小而增大
- 最后线性组合f(x)实现M个基本你分类器的加权表权,α表示基本分类器GM(x)G_M(x)GM(x)的重要性(AdaBoost特性2 基本分类器的加权线性组合)

8.1.3 AdaBoost案例
例8.1 给定如表8.1所示训练数据。假设弱分类器由<v或r>v产生,其阈值u使该分类器在训练数据集上分类误差率最低。试用AdaBoost算法学习一个强分类器。

其中Z1和W21的计算方式

8.2 AdaBoost训练误差分析
【定理8.1】训练误差界
直接给出结论:最终分类器会有一个训练误差上界

证明如下,核心的点包括:
- 放缩:大于等于1,可以看到这个形式放缩,像极了我们前面计算数据集权值的形式。
- 所以,基于类似的形式,通过8.4式子得到变形式,通过递推直接发现就是Zi的相乘, 证毕。

【定理8.2】二类分类问题训练误差界

这里无非就是二类分类问题,核心的点:
- 通过yiGm(xi)y_iG_m(x_i)yiGm(xi)的等价分类函数,对Zm进行展开,然后进一步可以通过em误差率表示
- α代入
- γm=12−emγ_m=\frac{1}{2}-e_mγm=21−em换元,通过泰勒展开式得到的不等式得到。

推论
- 对求和进行放大了

8.3 AdaBoost算法解释
8.3.1 前向分布算法
- 从另一个方面理解,AdaBoost模型是加法模型,损失函数是指数函数,学习算法是前向分布算法的二类学习方法
加法模型:
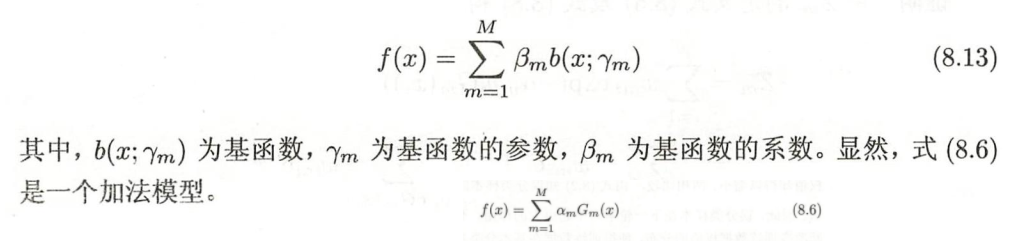 ·
·
而学习加法模型,给定损失函数L(x, f(x))情况下,学习加法模型就是经验风险最小化问题(损失函数极小化问题)
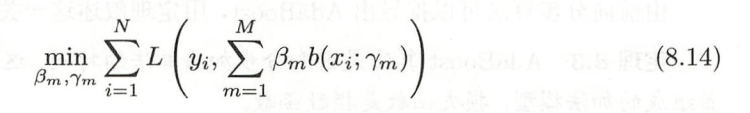
- 但现实,这个是求不出来的,考虑使用前向分布算法求解该优化问题:从前向后每一步只学习到一个基函数和稀疏,逐步逼近优化目标函数,从而简化优化的复杂度,即优化损失函数:
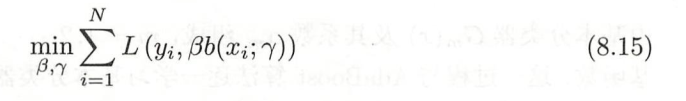
从而得到前向分布算法。
【算法8.2 前向分布算法】
- 可以看到,核心思想很简单,就是将求解最优化问题的所有参数βm,γmβ_m, γ_mβm,γm优化为以此求解各个参数的问题。

8.3.2 前向分布算法和AdaBoost
前面是理论铺垫,接下来通过该算法讲述如何推导出AdaBoost模型。
【定理8.3】 AdaBoost算法是前向分布加法

证明如下:
AdaBoost最终分类器,和前向分布算法的想法很像,都是逐步学习基函数。
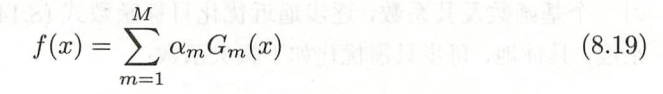
接下来证明前向分布算法的损失函数是指数损失函数时,前向分布算法学习过程等价于AdaBoost算法。
首先做出铺垫工作,主要是描述了逐步迭代的思想,以及指数损失的等价描述,指出wmiw_miwmi与最小化问题无关。

现证 使式(8.21)达到最小的am∗a_m^*am∗和Gm∗(x)G_m^*(x)Gm∗(x)就是 AdaBoost 算法所得到的ama_mam和Gm(x)G_m(x)Gm(x)。求解式(8.21)可分两步:
- 第一步是说,指数损失函数与01损失函数可替换
- 最关键的一步是8.22式,可以参考8.11和8.21式子得到
- 代入G后,求导为0,得到最小的α,发现与AdaBoost对应的形式,完全一致。证毕
 α求导过程
α求导过程
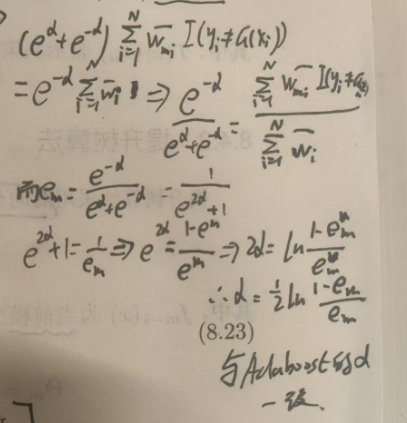
8.4 提升树
- 提升树是以分类树或者回归树为基本分类器的Boosting,是统计学习方法中性能最好的方法之一
8.4.1 提升树模型
- 前面提到,Boosting采用加法模型(基函数线性组合)和前向分布算法。
- 而以决策树为基础函数的Boosting称为提升树
- 分类问题决策树为二叉分类树
- 回归问题决策树为二叉回归树
- 提升树模型可以看成决策树的加法模型

8.4.2 提升树算法
- 初步确定提升树f0(x)=0f_0(x)=0f0(x)=0,得到第m步的模型如下图
- 其中fm−1(x)f_{m-1}(x)fm−1(x)表示当前模型,通过经验风险最小化得到下一个决策树的参数ΘmΘ_mΘm
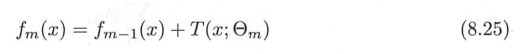
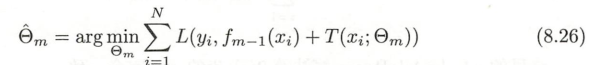
- 最终通过树的线性组合来更好的拟合训练数据,接下来说明针对不同问题提升树的学习算法,主要区别是使用的损失函数不同
- 回归问题:平方损失函数(本小节讨论)
- 分类问题:指数损失函数(AdaBoost基本分类器为二类分类树)
- 一般决策问题:一般损失函数(梯度提升)
- 如果将输入空间划分为J个互不相交的区域R1,R2...,RjR_1,R_2...,R_jR1,R2...,Rj,在每个区域确定一个常量cjc_jcj,树可以表示为如下
- Θ=(R1,C1),(R2,C2),...,(RJ,CJ)Θ={(R_1, C_1), (R_2, C_2),...,(R_J,C_J)}Θ=(R1,C1),(R2,C2),...,(RJ,CJ)表示树的区域划分和各个区域的常数。J表示树的叶子结点个数(即回归树的复杂度)
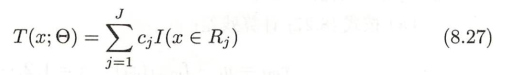
- 回归树提升树可以使用前向分布算法,套用上述的模型得到:
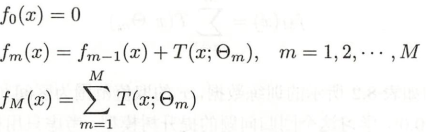
- 然后根据前m-1步,求解第m步时,即要求解最优化问题:进而确定第m颗树的参数ΘmΘ_mΘm
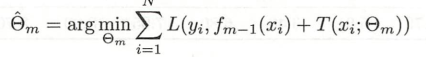
采用平方误差损失函数时,对应的损失就是如下形式
注:这里将y−fm−1(x)y-f_{m-1}(x)y−fm−1(x)定义为模型拟合数据的
残差(即真实值和预测值的差,后续学到GBDT算法也是会用到这种思想),对于回归问题的提升树,在这个式子中,就可以看成是模拟当前模型的残差,从而简化提升树的算法
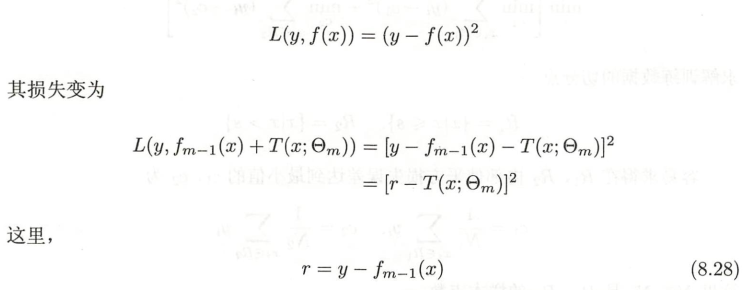
根据上述分析,就可以推导出回归问题提升树相关的算法如下:
【算法8.3 回归问题提升树算法】

给出一个例子
- 在前面划分树的时候提过,这里的R1和R2对应的是划分的域,然后c1和c2对应的是划分的域中的均值
- 理解:内层的min是为了穷尽划分,外层的min是为了求解最优划分
- 得到回归树后(划分区域内填充均值),然后进而得到残差表,得到此时的平方损失误差
- 接下来是要进行**
拟合残差**,按照同样的求解思路,得到最优划分点,以及对应的均值 - 如此循环,直到损失误差满足条件(感受前向分布算法,逐步求解参数的思路)


8.4.3 梯度提升
- 前面提到,提升树通过加法模型和前向分布算法实现学习的优化过程,并通过平方损失函数实现回归,本小节介绍在一般损失函数下的处理——
梯度提升 - 这是利用最速下降法的近似方法, 核心思想是通过损失函数的负梯度−[∂L(y,f(xi))∂f(xi)]f(x)=fm−1(x)-\left[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}\right]_{f(x)=f_{m-1}(x)}−[∂f(xi)∂L(y,f(xi))]f(x)=fm−1(x)作为当前模型中的值来作为
回归问题提升树残差的近似值
【算法8.4 梯度提升算法】
- 首先初始化,这里的L是一般损失函数,此时是只有一个根节点的树
- 接下来第二步
- a:计算损失函数的负梯度来作为残差的估计
- b:通过残差rmir_{mi}rmi作为拟合第m颗树的叶节点区域RmjR_{mj}Rmj(平方损失函数就是残差,而对于一般损失函数来说是近似值)
- c:通过线性搜索估计叶节点区域的值,使得损失函数最小
- d:前向分布算法更新回归树(对应一次空间的划分,即叶节点区域)
- 第三步,得到最终的回归树









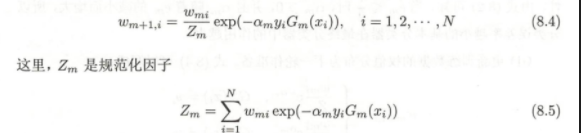
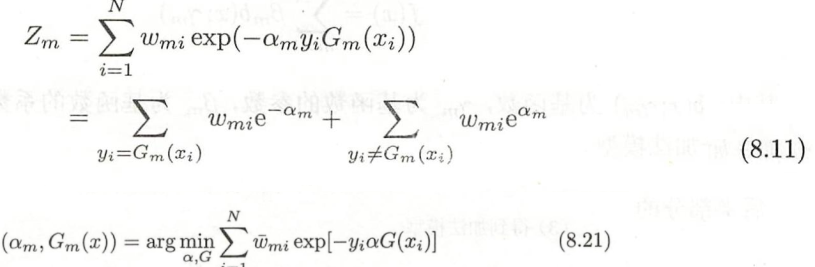
















 295
295

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








