本文深入探讨了随机变量的数学期望和方差，包括离散型和连续型随机变量的期望计算及其性质。同时，介绍了随机变量函数的期望、方差的定义和性质，并列举了几何分布等常见分布的期望与方差。此外，还讨论了矩、协方差、相关系数的概念及其性质，以及独立与不相关的概念。
随机变量的数字特征
随机变量的数学期望和方差
数学期望
离散型
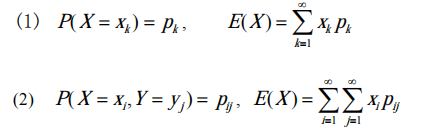
连续型
数学期望的性质
随机变量函数的期望
离散型
连续型
随机变量的方差
定义
D X = E ( X − E X ) 2 = E X 2 − ( E X ) 2 DX=E(X-EX)^2=EX^2-(EX)^2 DX=E(X−EX)2=EX2−(EX)2称为X的方差。
性质
一般情况下
D
(
X
±
Y
)
=
D
X
+
D
Y
±
2
c
o
v
(
X
,
Y
)
D(X\pm Y)=DX+DY\pm2cov(X,Y)
D(X±Y)=DX+DY±2cov(X,Y)
常见分布的期望与方差
其中
q
=
1
−
p
q=1-p
q=1−p
(7) 几何分布：
P
{
X
=
k
}
=
p
(
1
−
p
)
k
−
1
,
k
=
1
,
2
,
.
.
.
,
0
<
p
<
1
P\{X=k\}=p(1-p)^{k-1},k=1,2,...,0<p<1
P{X=k}=p(1−p)k−1,k=1,2,...,0<p<1
E
X
=
1
p
,
D
X
=
1
−
p
p
2
EX={1\over p},DX={{1-p}\over p^2}
EX=p1,DX=p21−p
矩、协方差和相关系数
矩
协方差
c
o
v
(
X
,
Y
)
=
E
(
X
−
E
X
)
(
Y
−
E
Y
)
=
E
X
Y
−
E
X
E
Y
cov(X,Y)=E(X-EX)(Y-EY)=EXY-EXEY
cov(X,Y)=E(X−EX)(Y−EY)=EXY−EXEY
特别的，
c
o
v
(
X
,
X
)
=
D
X
cov(X,X)=DX
cov(X,X)=DX
性质
相关系数
对于随机变量X和Y，如果D(X)D(Y)
≠
\ne
= 0,则有相关系数：
如果D(X)D(Y)=0，则相关系数为0.
性质
- ρ X Y ≤ 1 \rho_{XY}\le1 ρXY≤1;
- ρ X Y = 1 \rho_{XY}=1 ρXY=1的充要条件是存在不全为0的常数a和b，使得 P { a X + b Y = 1 } = 1. P\{aX+bY=1\}=1. P{aX+bY=1}=1.
独立与不相关
扫一扫
3011
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
