机器人-关节空间轨迹规划

机器人工作时，已知机器人各关节的初始位置便可以根据机器人的正运动方程求解出机器人末端的末端位姿。知道到机器人末端执行器的初始位姿和末端位姿就可以规划出机器人从初始位姿到达期望位姿的轨迹。

本节将介绍关节空间轨迹规划并使用MATLAB进行仿真。

关节空间轨迹规划用函数$jtraj$来表示，函数$jtraj$的调用格式为$\left[\begin{array}{ccc}qq& dq& dd\end{array}\right]=jtraj\left(qz,qn,t\right)$，从$qz$到$qn$的两个位姿之间进行平滑插值，就可以得到一个关节空间轨迹，$q、qd、qdd$分别为规划的位移、速度和加速度，$t$为时间。

在这里我取的始末位置为：

qz = [0 0 0 0 0];    %初始位姿
qn = [pi/2 -pi/2 pi/6 pi/12 0];    %末端位姿

运行下面的程序：

% 关节空间轨迹规划
clc
clear
L(1) = Link([0 0 0 -pi/2 0]);
L(2) = Link([0 0 1.2 0 0]);
L(3) = Link([0 0 1 0 0]);
L(4) = Link([0 0 0 pi/2 0]);
L(5) = Link([0 0 0 0 0]);
h = SerialLink(L, 'name', 'fivelink');
t = 0:0.01:2;    %采样时间为2s，采样间隔为0.01s
qz = [0 0 0 0 0];    %初始位姿
qn = [pi/2 -pi/2 pi/6 pi/12 0];    %末端位姿
[q, qd, qdd] = jtraj(qz, qn, t);    %轨迹规划
plot(h,q,'trail','b-')    %图形演示
T = fkine(h, q);    %生成三维矩阵
%取机械臂末端执行器位置所标矩阵
m = squeeze(T(:,4,:));   % 末端执行器坐标的变化曲线
plot(t, m);    %绘制机械臂末端执行器空间轨迹
%生成关节i(i=1, 2, 3, 4, 5)的角位移曲线
figure(2);
subplot(3,1,1);
plot(t,q(:,1),'r','LineWidth',1);
title('关节1位移变化曲线');
%生成关节i(i=1, 2, 3, 4, 5)的角速度曲线
subplot(3,1,2);
plot(t,qd(:,1),'g','LineWidth',1);
title('关节1速度变化曲线');
%生成关节i(i=1, 2, 3, 4, 5)的角加速度曲线
subplot(3,1,3);
plot(t,qdd(:,1),'b','LineWidth',1);
title('关节1加速度变化曲线');

运行结果：

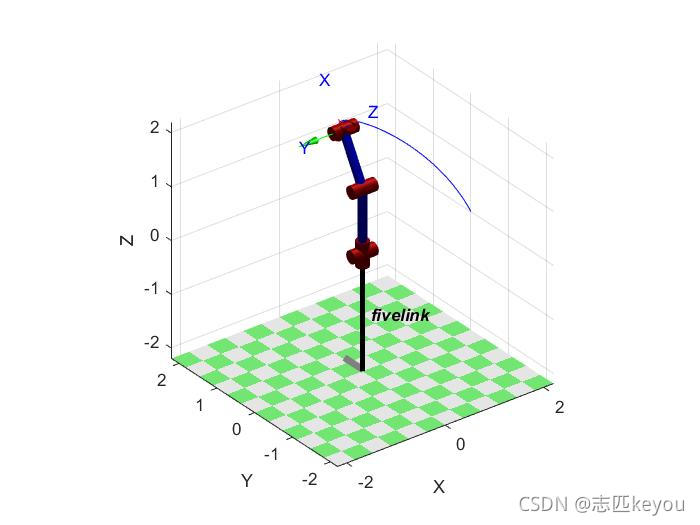
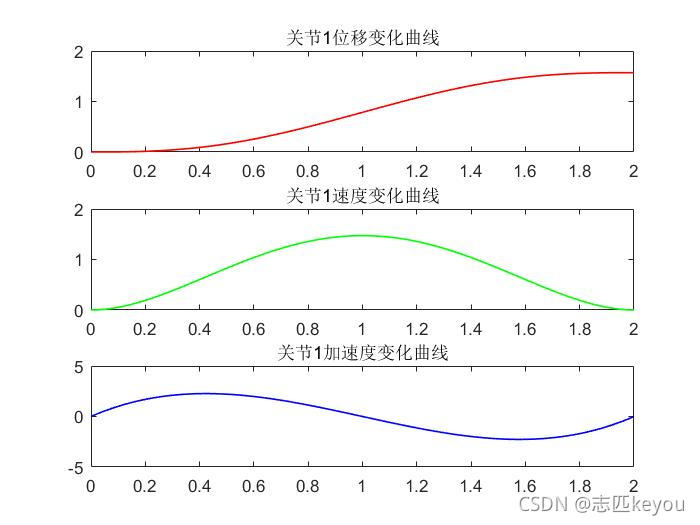
注：

• 运行之前需在命令行窗口输入$startup\_rvc$运行机器人工具箱
• 若要得到关节2、3、4、5关节的位移、速度、加速度曲线，需将后面的代码进行替换

%生成关节i(i=1, 2, 3, 4, 5)的角位移曲线
figure(2);
subplot(3,1,1);
plot(t,q(:,2),'r','LineWidth',1);
title('关节2位移变化曲线');
%生成关节i(i=1, 2, 3, 4, 5)的角速度曲线
subplot(3,1,2);
plot(t,qd(:,2),'g','LineWidth',1);
title('关节2速度变化曲线');
%生成关节i(i=1, 2, 3, 4, 5)的角加速度曲线
subplot(3,1,3);
plot(t,qdd(:,2),'b','LineWidth',1);
title('关节2加速度变化曲线');

关节3、4、5同理，下节讲述笛卡尔坐标系轨迹规划。