系列文章目录
文章目录
前言
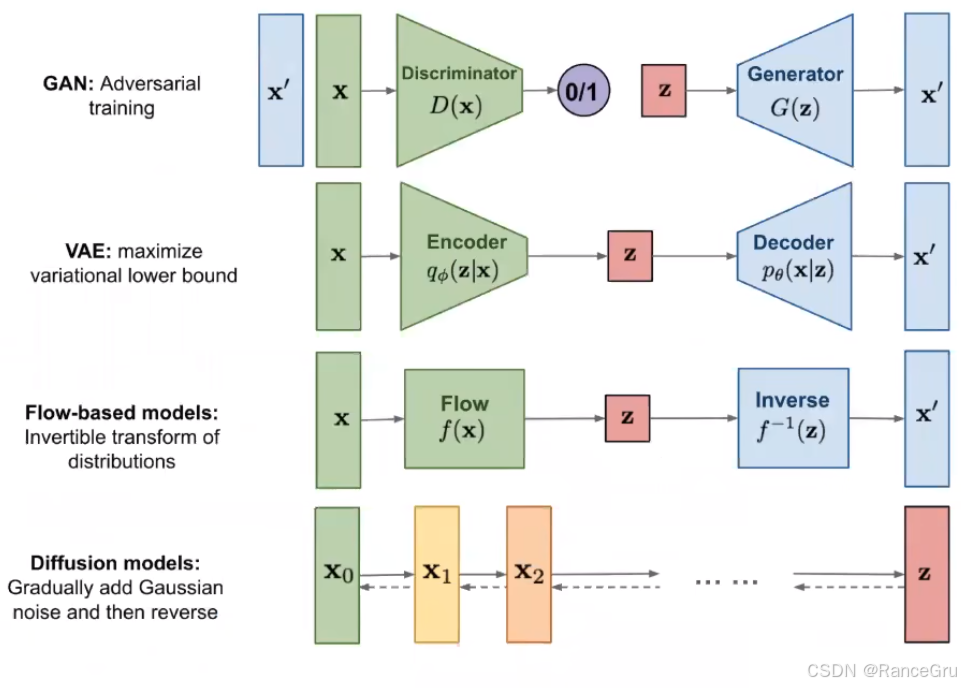
深度生成模型是人工智能领域的重要分支,它通过学习数据的潜在分布来生成新的数据样本。
-
GAN:博弈中的创造
GAN的创新在于其“左右互博”的对抗训练机制。生成器Generator负责制造“假数据”,而判别器Discriminator则负责甄别数据的真伪。二者相互博弈、共同进化,最终目标是让生成器能产出以假乱真的结果。这种机制使得GAN在图像生成上表现出色,能产生细节非常逼真的样本。但其主要挑战在于训练过程可能不稳定,且容易发生“模式崩溃”,且生成器只产生少数几种类型的样本,缺乏多样性,其训练难度限制了其在超大模型时代的普及。。 -
VAE:概率世界的编码器
VAE的核心思想是将输入数据映射到一个概率潜在空间,通常假设服从高斯分布。它包含编码器和解码器。编码器将输入数据压缩为潜在空间中的均值和方差参数,然后从该分布中采样得到一个潜在向量,解码器再尝试从这个向量重构出原始数据。VAE的优势在于训练过程相对稳定,并且学习到的隐变量空间具有良好的数学意义,便于数据插值和探索。但其生成的结果有时会显得比较模糊或平滑,不如GAN生成的样本锐利。 -
Flow:精确的变量变换
流模型Flow-based Models旨在通过一系列可逆的数学变换,将一个简单的基础分布精确地转化为复杂的数据分布。因为每一步变换都是可逆的,所以模型可以精确地计算任何数据点的概率密度(对数似然),而无需近似。这也意味着隐变量和数据点具有完全相同的维度,并且可以通过逆变换从隐变量精确地生成数据。但其挑战在于,可逆变换的设计要求很高,通常计算成本也较大。 -
Diffusion:去噪中的艺术
扩散模型Diffusion Models是当前的热点,其灵感来源于非平衡热力学。它包含两个过程:前向过程是逐步向原始数据添加噪声,直至数据完全变为随机噪声;反向过程则是学习如何从噪声中一步步地去除噪声,恢复出原始数据结构。模型学习的核心就是这个去噪的过程。扩散模型的优势在于训练目标简单且稳定,生成的样本多样性和质量都非常高。其主要缺点是生成速度相对较慢,因为它通常需要数百甚至上千步的去噪迭代才能得到最终结果。
一、UNet模型
1、经典UNet结构
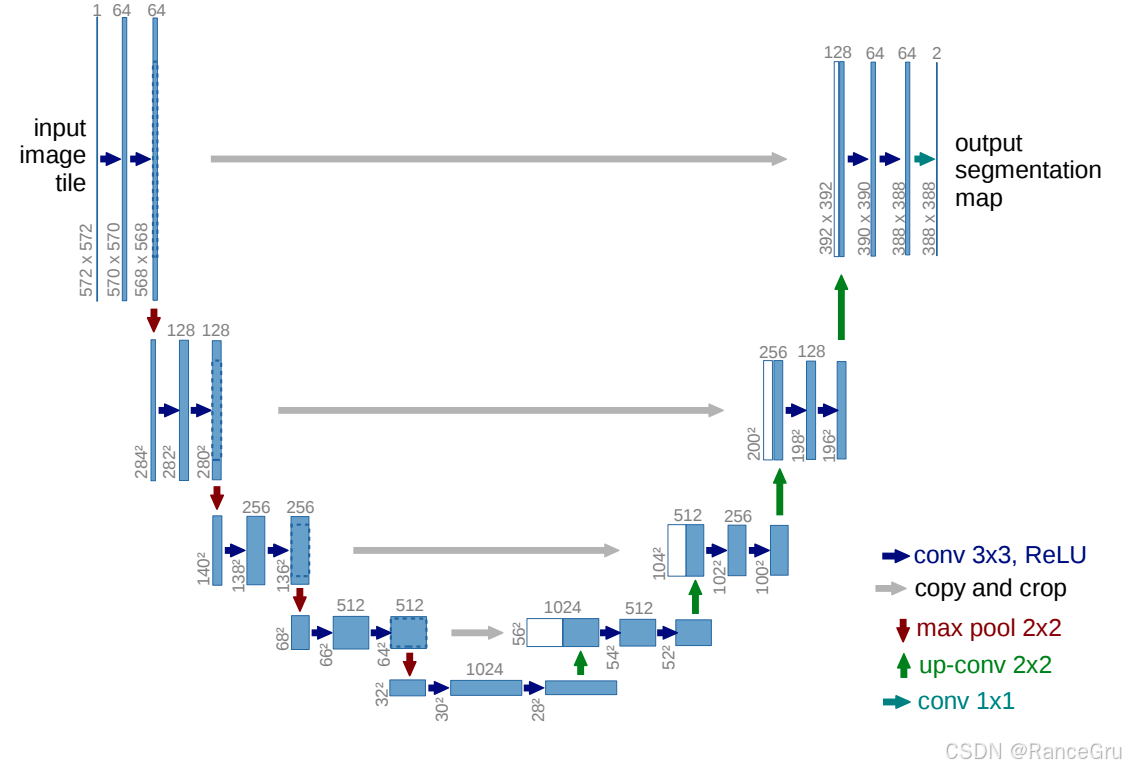
阶段一:输入572×572×1的单通道灰度图,进行两次连续的无padding3×3卷积+ReLU激活函数组成,通道数从1增加到64。
阶段二:对阶段一的输出进行2×2最大池化下采样操作,进行两次连续的无padding3×3卷积+ReLU激活函数组成,通道数从64增加到128。
阶段三:对阶段二的输出进行2×2最大池化下采样操作,进行两次连续的无padding3×3卷积+ReLU激活函数组成,通道数从128增加到256。
阶段四:对阶段三的输出进行2×2最大池化下采样操作,进行两次连续的无padding3×3卷积+ReLU激活函数组成,通道数从256增加到512。
阶段五:对阶段四的输出进行2×2最大池化下采样操作,进行两次连续的无padding3×3卷积+ReLU激活函数组成,通道数从512增加到1024。
阶段六:对阶段五的输出进行2×2转置卷积上采样操作且通道数减半,使用跳跃连接操作+裁剪操作将阶段四的输出特征图与上采样特征图进行拼接。再进行两次连续的无padding3×3卷积+ReLU激活函数组成,通道数从1024减少到512。
阶段七:对阶段六的输出进行2×2转置卷积上采样操作且通道数减半,使用跳跃连接操作+裁剪操作将阶段四的输出特征图与上采样特征图进行拼接。再进行两次连续的无padding3×3卷积+ReLU激活函数组成,通道数从512减少到256。
阶段八:对阶段七的输出进行2×2转置卷积上采样操作且通道数减半,使用跳跃连接操作+裁剪操作将阶段四的输出特征图与上采样特征图进行拼接。再进行两次连续的无padding3×3卷积+ReLU激活函数组成,通道数从256减少到128。
阶段九:对阶段八的输出进行2×2转置卷积上采样操作且通道数减半,使用跳跃连接操作+裁剪操作将阶段四的输出特征图与上采样特征图进行拼接。再进行两次连续的无padding3×3卷积+ReLU激活函数组成,通道数从128减少到64。最后使用一个1×1卷积操作进行处理,得到最终的输出特征图,输出通道数为2。
在上采样时使用的裁剪操作,属于中心裁剪操作:
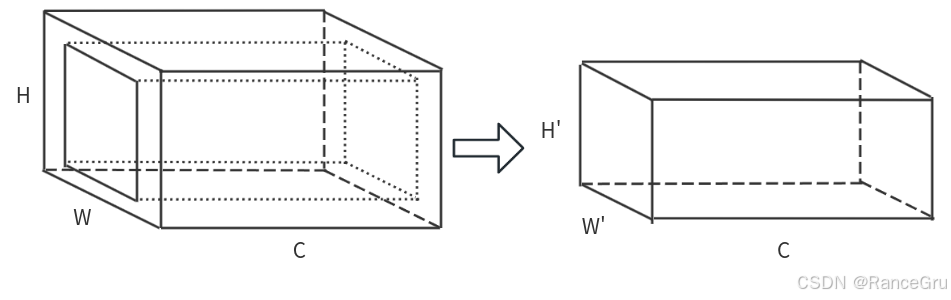
UNet模型的左侧路径为编码器,作用是特征提取和降维,将图像信息压缩成一个小的、但具有大量通道数的高维特征图。
UNet模型的右侧路径为解码器,作用是特征融合和上采样,将压缩的特征恢复为原始输入图像大小的像素级分类结果,精确地还原物体的边缘细节。
现阶段的UNet模型结构对原始的UNet模型结构有进一步优化,主要使用padding+3×3卷积+BN+ReLU激活函数,这样可以避免每个阶段的特征图尺寸缩小问题、特征丢失问题以及多余的裁剪操作,在加强特征提取能力的同时还可以让输入和输出大小一致。
二、DDPM模型
Denoising Diffusion Probabilistic Models,DDPM是扩散模型的一种,在视觉领域是属于生成式的模型。
扩散模型中最重要的思想根基是马尔可夫链,它的一个关键性质是平稳性。即如果一个概率随时间变化,那么在马尔可夫链的作用下,它会趋向于某种平稳分布,时间越长,分布越平稳。
DDPM的核心思想可以简单理解为让模型学会一步步地把一张完全噪声的图片去噪还原成清晰的图片,从而掌握图片的生成能力。
所以DDPM模型的的结构主要包含两个部分,即前向加噪过程和反向去噪过程。
1、Diffusion前向加噪
前向加噪可以理解为一种特殊的分子扩散运动,所谓分子扩散运动本质是物质分子从高浓度区域自发地、永不停息地运动到低浓度区域,直到分布均匀为止。由于分子的无规则扩散运动,液体中的紫色分子会随机地向四周扩散,经过足够长的时间,溶液中任何一处的紫色分子的浓度达到动态平衡。
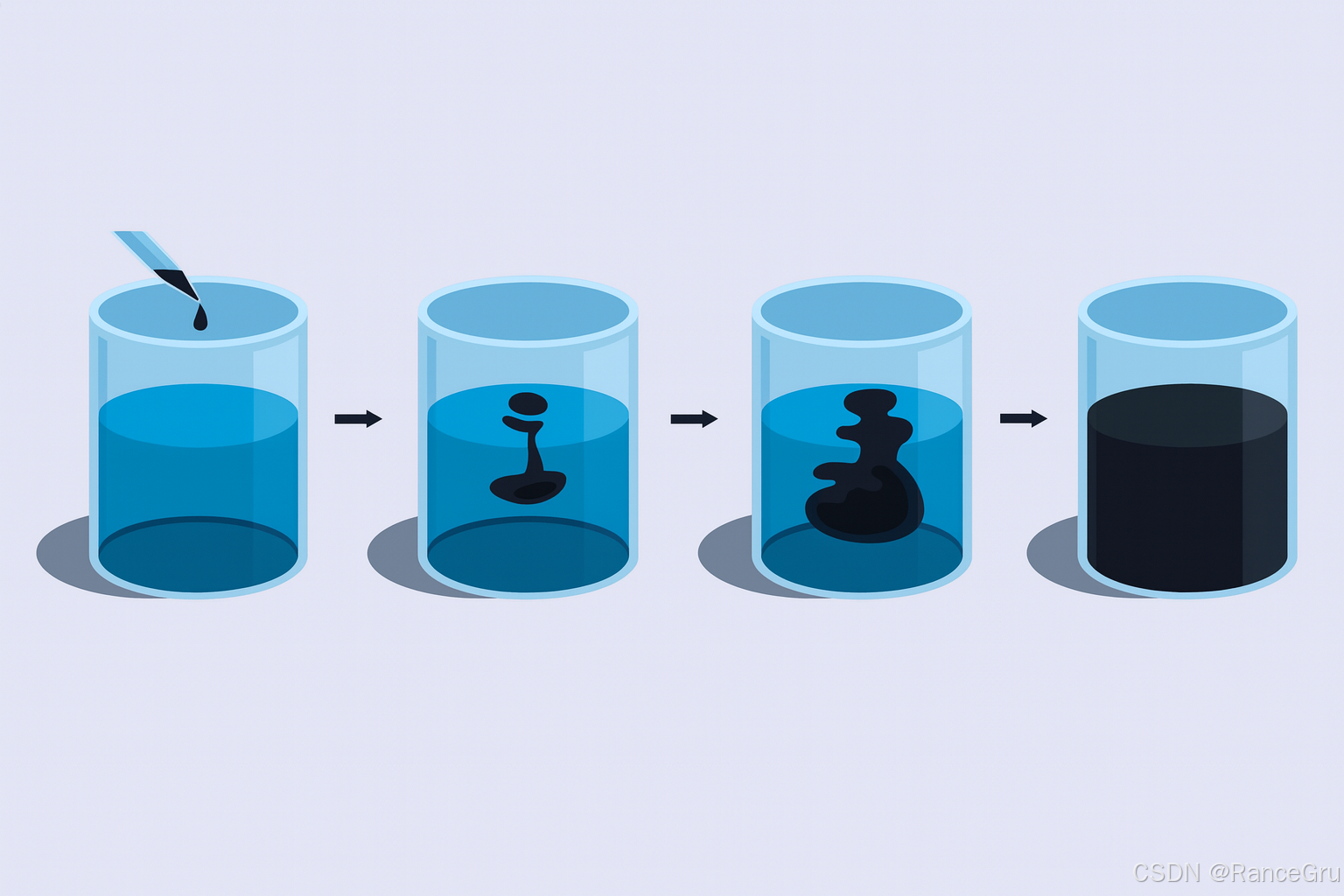
通过一系列步骤,逐步向清晰图片中添加微小的高斯噪声,直到图片完全变成一个无法辨认的随机噪声图 。

X
t
=
f
(
X
t
−
1
)
=
1
−
β
t
∗
X
t
−
1
+
β
t
∗
Z
t
Z
t
∼
N
(
0
,
I
)
X_t = f(X_{t-1})= \sqrt{1-\beta_t}\ast X_{t-1}+\sqrt{\beta_t}\ast Z_t \ \ \ \ \ \ \ \ \ Z_t\sim N(0,I)
Xt=f(Xt−1)=1−βt∗Xt−1+βt∗Zt Zt∼N(0,I)
X
t
X_t
Xt、
X
t
−
1
X_{t-1}
Xt−1:分别表示时间步t和t−1的状态变量。
X
0
X_0
X0通常代表第0步的原始图像数据,而
X
t
X_t
Xt是从第0步逐步累加噪声直到第t步的图像数据。
β
t
\beta_t
βt:是一个超参数,满足0<
β
t
\beta_t
βt<1,通常随着时间步t的增加而单调递增,使得越到后面扩散速度越快。
β
t
\beta_t
βt负责控制噪声添加的强度,
β
t
\beta_t
βt越小,过程越保留前状态,
β
t
\beta_t
βt越大,噪声占主导。
Z
t
Z_t
Zt:是一个随机噪声项,服从标准多元正态分布,即均值为0、协方差矩阵为单位矩阵
I
I
I。这表示噪声是独立同分布的,每个维度互不相关。
该公式描述了一个随机过程,定义了当前状态变量 X t X_t Xt如何从上一个状态 X t − 1 X_{t-1} Xt−1通过添加噪声演变而来。
α
t
=
1
−
β
t
\alpha_t = 1-\beta_t
αt=1−βt
将
1
−
β
t
1-\beta_t
1−βt转换为
α
t
\alpha_t
αt,方便计算与观察。
X
t
=
α
t
∗
X
t
−
1
+
1
−
α
t
∗
Z
t
X_t = \sqrt{\alpha_t}\ast X_{t-1}+\sqrt{1-\alpha_t}\ast Z_t
Xt=αt∗Xt−1+1−αt∗Zt
X
t
−
1
=
α
t
−
1
∗
X
t
−
2
+
1
−
α
t
−
1
∗
Z
t
−
1
X_{t-1} = \sqrt{\alpha_{t-1}}\ast X_{t-2}+\sqrt{1-\alpha_{t-1}}\ast Z_{t-1}
Xt−1=αt−1∗Xt−2+1−αt−1∗Zt−1
把
α
t
\alpha_t
αt代入到
X
t
X_{t}
Xt公式中,并按相同逻辑推导出
X
t
−
1
X_{t-1}
Xt−1公式。
X
t
=
α
t
∗
(
α
t
−
1
∗
X
t
−
2
+
1
−
α
t
−
1
∗
Z
t
−
1
)
+
1
−
α
t
∗
Z
t
X_t = \sqrt{\alpha_t}\ast (\sqrt{\alpha_{t-1}}\ast X_{t-2}+\sqrt{1-\alpha_{t-1}}\ast Z_{t-1})+\sqrt{1-\alpha_t}\ast Z_t
Xt=αt∗(αt−1∗Xt−2+1−αt−1∗Zt−1)+1−αt∗Zt
=
α
t
α
t
−
1
∗
X
t
−
2
+
α
t
−
α
t
α
t
−
1
∗
Z
t
−
1
+
1
−
α
t
∗
Z
t
= \sqrt{\alpha_t\alpha_{t-1}}\ast X_{t-2}+\sqrt{\alpha_t-\alpha_t\alpha_{t-1}}\ast Z_{t-1}+\sqrt{1-\alpha_t}\ast Z_t
=αtαt−1∗Xt−2+αt−αtαt−1∗Zt−1+1−αt∗Zt
使用
X
t
−
1
X_{t-1}
Xt−1公式替代
X
t
X_{t}
Xt公式中的
X
t
−
1
X_{t-1}
Xt−1参数,并简化得到新的
X
t
X_{t}
Xt公式。
1
−
α
t
∗
Z
t
∼
N
(
0
,
(
1
−
α
t
)
∗
I
)
\sqrt{1-\alpha_t}\ast Z_t\sim N(0,(1-\alpha_t)\ast I)
1−αt∗Zt∼N(0,(1−αt)∗I)
α
t
−
α
t
α
t
−
1
∗
Z
t
−
1
∼
N
(
0
,
(
α
t
−
α
t
α
t
−
1
)
∗
I
)
\sqrt{\alpha_t-\alpha_t\alpha_{t-1}}\ast Z_{t-1}\sim N(0,(\alpha_t-\alpha_t\alpha_{t-1})\ast I)
αt−αtαt−1∗Zt−1∼N(0,(αt−αtαt−1)∗I)
(
α
t
−
α
t
α
t
−
1
∗
Z
t
−
1
+
1
−
α
t
∗
Z
t
)
∼
N
(
0
,
(
1
−
α
t
α
t
−
1
)
∗
I
)
(\sqrt{\alpha_t-\alpha_t\alpha_{t-1}}\ast Z_{t-1}+\sqrt{1-\alpha_t}\ast Z_t)\sim N(0,(1-\alpha_t\alpha_{t-1})\ast I)
(αt−αtαt−1∗Zt−1+1−αt∗Zt)∼N(0,(1−αtαt−1)∗I)
基于噪声项的正态分布和正态分布的可加性,使得每个缩放噪声项服从正态分布,方差为缩放因子的平方。
X
t
−
1
=
α
t
α
t
−
1
∗
X
t
−
2
+
1
−
α
t
α
t
−
1
∗
Z
Z
∼
N
(
0
,
I
)
X_{t-1}=\sqrt{\alpha_t\alpha_{t-1}}\ast X_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}\ast Z \ \ \ \ \ \ \ \ \ Z\sim N(0,I)
Xt−1=αtαt−1∗Xt−2+1−αtαt−1∗Z Z∼N(0,I)
X
t
=
α
t
α
t
−
1
.
.
.
α
1
∗
X
0
+
1
−
α
t
α
t
−
1
.
.
.
α
1
∗
Z
Z
∼
N
(
0
,
I
)
X_{t}=\sqrt{\alpha_t\alpha_{t-1}...\alpha_1}\ast X_{0}+\sqrt{1-\alpha_t\alpha_{t-1}...\alpha_1}\ast Z \ \ \ \ \ \ \ \ \ Z\sim N(0,I)
Xt=αtαt−1...α1∗X0+1−αtαt−1...α1∗Z Z∼N(0,I)
X
t
=
α
t
‾
∗
X
0
+
1
−
α
t
‾
∗
Z
Z
∼
N
(
0
,
I
)
X_t = \sqrt{\overline{\alpha_t}}\ast X_{0}+\sqrt{1-\overline{\alpha_t}}\ast Z \ \ \ \ \ \ \ \ \ Z\sim N(0,I)
Xt=αt∗X0+1−αt∗Z Z∼N(0,I)
根据
X
t
X_{t}
Xt到
X
t
−
1
X_{t-1}
Xt−1的逻辑,可以推广到任意步长逐步回溯
X
0
X_0
X0。把累积乘积
α
n
\alpha_n
αn抽象为
α
t
‾
\overline{\alpha_t}
αt。同样因为
Z
Z
Z是随机的,所以可以把
Z
Z
Z和
I
I
I抽象出来。
最后的公式表示 X t X_{t} Xt可直接从 X 0 X_{0} X0通过一次线性变换生成,其中噪声水平由 α t ‾ \overline{\alpha_t} αt控制(当 t增大时, α t ‾ \overline{\alpha_t} αt→0,即 X t X_{t} Xt趋近于纯噪声)。也就是说可以直接从原图 X 0 X_0 X0一步计算生成第 t t t步之后的扩散图 X t X_t Xt,而不需要再一步接一步的计算每次的扩散。
2、Reverse反向去噪

X
0
=
X
t
−
1
−
α
t
‾
∗
Z
α
t
‾
Z
∼
N
(
0
,
I
)
X_0 = \frac{X_t-\sqrt{1-\overline{\alpha_t}}\ast Z}{\sqrt{\overline{\alpha_t}}} \ \ \ \ \ \ \ \ \ Z\sim N(0,I)
X0=αtXt−1−αt∗Z Z∼N(0,I)
按照上面扩散逻辑的推理公式,通过反转公式可以直接从噪声图 X t X_t Xt一步计算出目标图 X 0 X_0 X0,但是在实际实验中这么做的得到的效果无法让人满意,且不符合逆扩散的过程,所以反而需要一步一步推。
P
(
A
∣
B
)
=
P
(
A
⋂
B
)
P
(
B
)
P(A\mid B) = \frac{P(A\bigcap B)}{P(B)}
P(A∣B)=P(B)P(A⋂B)
P
(
B
∣
A
)
=
P
(
A
⋂
B
)
P
(
A
)
P(B\mid A) = \frac{P(A\bigcap B)}{P(A)}
P(B∣A)=P(A)P(A⋂B)
P
(
A
∣
B
)
=
P
(
A
⋂
B
)
P
(
B
)
=
P
(
B
∣
A
)
P
(
A
)
P
(
B
)
P(A\mid B) = \frac{P(A\bigcap B)}{P(B)} = \frac{P(B\mid A)P(A)}{P(B)}
P(A∣B)=P(B)P(A⋂B)=P(B)P(B∣A)P(A)
以上是一个标准的概率论贝叶斯定理的推导过程。
P
(
X
t
−
1
∣
X
t
)
=
P
(
X
t
∣
X
t
−
1
)
P
(
X
t
−
1
)
P
(
X
t
)
P(X_{t-1}\mid X_t) = \frac{P(X_t\mid X_{t-1})P(X_{t-1})}{P(X_t)}
P(Xt−1∣Xt)=P(Xt)P(Xt∣Xt−1)P(Xt−1)
P
(
X
t
−
1
∣
X
t
,
X
0
)
=
P
(
X
t
∣
X
t
−
1
,
X
0
)
P
(
X
t
−
1
∣
X
0
)
P
(
X
t
∣
X
0
)
P(X_{t-1}\mid X_t,X_0) = \frac{P(X_t\mid X_{t-1},X_0)P(X_{t-1}\mid X_0)}{P(X_t\mid X_0)}
P(Xt−1∣Xt,X0)=P(Xt∣X0)P(Xt∣Xt−1,X0)P(Xt−1∣X0)
根据以上的贝叶斯定理的逻辑,推广到时间序列中的条件概率,使得能够描述
X
t
X_t
Xt和
X
t
−
1
X_{t-1}
Xt−1状态之间的概率关系,且在条件于
X
0
X_0
X0时正确。
P
(
X
t
∣
X
t
−
1
)
∼
N
(
α
t
∗
X
t
−
1
,
(
1
−
α
t
)
∗
I
)
P(X_t\mid X_{t-1})\sim N(\sqrt{\alpha_t}\ast X_{t-1},(1-\alpha_t)\ast I)
P(Xt∣Xt−1)∼N(αt∗Xt−1,(1−αt)∗I)
P
(
X
t
∣
X
0
)
∼
N
(
α
t
‾
∗
X
0
,
(
1
−
α
t
‾
)
∗
I
)
P(X_t\mid X_{0})\sim N(\sqrt{\overline{\alpha_t}}\ast X_{0},(1-\overline{\alpha_t})\ast I)
P(Xt∣X0)∼N(αt∗X0,(1−αt)∗I)
P
(
X
t
−
1
∣
X
0
)
∼
N
(
α
t
−
1
‾
∗
X
0
,
(
1
−
α
t
−
1
‾
)
∗
I
)
P(X_{t-1}\mid X_{0})\sim N(\sqrt{\overline{\alpha_{t-1}}}\ast X_{0},(1-\overline{\alpha_{t-1}})\ast I)
P(Xt−1∣X0)∼N(αt−1∗X0,(1−αt−1)∗I)
结合以上计算的扩散模型前向定义和条件分布 P P P的表示,对于给定的前一个状态,统计当前状态的正态分布。
X
∼
N
(
μ
,
σ
2
)
X\sim N(\mu,\sigma^2)
X∼N(μ,σ2)
f
(
x
)
=
1
σ
2
π
e
−
1
2
(
x
−
μ
σ
)
2
f(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}
f(x)=σ2π1e−21(σx−μ)2
以上公式为服从正态分布的随机变量
x
x
x的概率密度函数,结合以上公式解释其中的参数:
x
x
x:随机变量可能的取值。
μ
\mu
μ:分布的均值或期望值。它决定了分布中心的位置。在您提供的扩散模型公式中,比如
α
t
∗
X
t
−
1
\sqrt{\alpha_t}\ast X_{t-1}
αt∗Xt−1就是均值。
σ
\sigma
σ:分布的标准差。它衡量了数据分布的离散程度,值越大,数据越分散。
σ
2
\sigma^2
σ2是标准差的平方,在扩散模型的公式中,就是
(
1
−
α
t
)
(1-\alpha_t)
(1−αt)方差。
π
\pi
π:圆周率,约等于 3.14159。
e
e
e:自然常数,约等于 2.71828。
P ( X t − 1 ∣ X t , X 0 ) = 1 1 − α t 2 π e − 1 2 ( x t − α t ∗ X t − 1 1 − α t ) 2 1 1 − α t − 1 ‾ 2 π e − 1 2 ( x t − 1 − α t − 1 ‾ ∗ X 0 1 − α t − 1 ‾ ) 2 1 1 − α t ‾ 2 π e − 1 2 ( x t − α t ‾ ∗ X 0 1 − α t ‾ ) 2 P(X_{t-1}\mid X_t,X_0) = \frac{\frac{1}{\sqrt{1-\alpha_t} \sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x_t-\sqrt{\alpha_t}\ast X_{t-1}}{\sqrt{1-\alpha_t}})^2}\frac{1}{\sqrt{1-\overline{\alpha_{t-1}}} \sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x_{t-1}-\sqrt{\overline{\alpha_{t-1}}}\ast X_{0}}{1-\overline{\alpha_{t-1}}})^2}}{\frac{1}{\sqrt{1-\overline{\alpha_t}} \sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x_t-\sqrt{\overline{\alpha_t}}\ast X_{0}}{1-\overline{\alpha_t}})^2}} P(Xt−1∣Xt,X0)=1−αt2π1e−21(1−αtxt−αt∗X0)21−αt2π1e−21(1−αtxt−αt∗Xt−1)21−αt−12π1e−21(1−αt−1xt−1−αt−1∗X0)2
= 1 1 − α t 1 − α t − 1 ‾ 1 − α t ‾ 2 π e − 1 2 ( ( x t − 1 − ( α t ( 1 − α t − 1 ‾ ) 1 − α t ‾ x t + α t − 1 ‾ ( 1 − α t ) 1 − α t ‾ x 0 ) ) 1 − α t 1 − α t − 1 ‾ 1 − α t ‾ ) 2 =\frac{1}{\frac{\sqrt{1-\alpha_t}\sqrt{1-\overline{\alpha_{t-1}}}}{\sqrt{1-\overline{\alpha_t}}} \sqrt{2\pi}}e^{-\frac{1}{2}(\frac{(x_{t-1}-(\frac{\sqrt{\alpha_t}(1-\overline{\alpha_{t-1}})}{1-\overline{\alpha_t}}x_t+\frac{\sqrt{\overline{\alpha_{t-1}}}(1-\alpha_t)}{1-\overline{\alpha_t}}x_0))}{\frac{\sqrt{1-\alpha_t}\sqrt{1-\overline{\alpha_{t-1}}}}{\sqrt{1-\overline{\alpha_t}}}})^2} =1−αt1−αt1−αt−12π1e−21(1−αt1−αt1−αt−1(xt−1−(1−αtαt(1−αt−1)xt+1−αtαt−1(1−αt)x0)))2
P ( X t − 1 ∣ X t , X 0 ) ∼ N ( ( α t ( 1 − α t − 1 ‾ ) 1 − α t ‾ x t + α t − 1 ‾ ( 1 − α t ) 1 − α t ‾ × X t − 1 − α t ‾ ∗ Z α t ‾ ) , ( 1 − α t 1 − α t − 1 ‾ 1 − α t ‾ ) 2 ) P(X_{t-1}\mid X_t,X_0)\sim N((\frac{\sqrt{\alpha_t}(1-\overline{\alpha_{t-1}})}{1-\overline{\alpha_t}}x_t+\frac{\sqrt{\overline{\alpha_{t-1}}}(1-\alpha_t)}{1-\overline{\alpha_t}}\times \frac{X_t-\sqrt{1-\overline{\alpha_t}}\ast Z}{\sqrt{\overline{\alpha_t}}}),(\frac{\sqrt{1-\alpha_t}\sqrt{1-\overline{\alpha_{t-1}}}}{\sqrt{1-\overline{\alpha_t}}})^2) P(Xt−1∣Xt,X0)∼N((1−αtαt(1−αt−1)xt+1−αtαt−1(1−αt)×αtXt−1−αt∗Z),(1−αt1−αt1−αt−1)2)
把 f ( x ) f(x) f(x)公式代入到 P ( X t − 1 ∣ X t , X 0 ) P(X_{t-1}\mid X_t,X_0) P(Xt−1∣Xt,X0)公式中进行简化计算,再根据概率密度函数 f ( x ) f(x) f(x)和 X ∼ N X\sim N X∼N的参数位置映射回 P ( X t − 1 ∣ X t , X 0 ) ∼ N P(X_{t-1}\mid X_t,X_0)\sim N P(Xt−1∣Xt,X0)∼N中,最后使用 x 0 x_0 x0的反转公式替换 x 0 x_0 x0。
P
(
X
t
−
1
∣
X
t
,
X
0
)
∼
N
(
(
α
t
(
1
−
α
t
−
1
‾
)
1
−
α
t
‾
x
t
+
α
t
−
1
‾
β
t
1
−
α
t
‾
×
X
t
−
1
−
α
t
‾
∗
Z
α
t
‾
)
,
β
t
1
−
α
t
−
1
‾
1
−
α
t
‾
)
P(X_{t-1}\mid X_t,X_0)\sim N((\frac{\sqrt{\alpha_t}(1-\overline{\alpha_{t-1}})}{1-\overline{\alpha_t}}x_t+\frac{\sqrt{\overline{\alpha_{t-1}}}\beta_t}{1-\overline{\alpha_t}}\times \frac{X_t-\sqrt{1-\overline{\alpha_t}}\ast Z}{\sqrt{\overline{\alpha_t}}}),\beta_t\frac{1-\overline{\alpha_{t-1}}}{1-\overline{\alpha_t}})
P(Xt−1∣Xt,X0)∼N((1−αtαt(1−αt−1)xt+1−αtαt−1βt×αtXt−1−αt∗Z),βt1−αt1−αt−1)
Z
=
U
N
e
t
(
x
t
,
t
)
Z = UNet(x_t,t)
Z=UNet(xt,t)
在以上公式中
α
t
\alpha_t
αt和
β
t
\beta_t
βt是已知的超参数,
x
t
x_t
xt是已知的噪声图,只有
Z
Z
Z是未知需要训练的参数,而
Z
Z
Z可以在UNet模型中训练。
3、IDDPM模型

1.自适应方差
在DDPM的反向去噪过程中,每一步加入的超参数噪声方差
α
t
\alpha_t
αt和
β
t
\beta_t
βt是固定的。这意味着模型只学习数据的均值(即预测噪声),而方差是预设的常数。
而IDDPM允许模型同时学习均值和高斯分布的方差。在实验中,模型学到的方差在最后几步会非常小,从而实现更精细的微调,显著提升了生成图像的清晰度和细节。
2.余弦噪声调度
在DDPM中使用的是线性调度,从 t=0到 t=T,噪声水平
β
t
\beta_t
βt从很小值线性增加到接近1。这会导致在过程的开始和结束阶段,噪声水平变化非常剧烈。
而在IDDPM中使用的是余弦调度,使用一个基于余弦函数的调度,使得噪声的变化在开始和结束时非常平缓,而在中间阶段变化相对较快。
相对于线性调度而言,其实余弦调度更符合人类的感知。
在扩散初期,图像被快速“破坏”成噪声是合理的;在扩散末期,对几乎已是纯噪声的图像只施加微小的改变。使得训练过程更稳定,生成效果更好。
3.优化的UNet
首次将 Transformer 的自注意力机制集成到了用于扩散模型的 UNet 中,这极大地提升了模型对图像全局一致性的建模能力,此时的结构已经具备了自注意力的 QKV。
4、DDIM模型

相对DDPM而言,DDIM 的优化不是对模型架构或训练过程的修改,而是对采样算法的根本性革新。
其核心思想是:重新定义前向过程,使其在训练目标不变的情况下,实现更高效的逆向采样。
DDPM的逆向过程使用的是马尔可夫链思想,必须一步接一步地从纯噪声 x t x_t xt迭代到清晰图像 x 0 x_0 x0。如果训练时用了1000步,前向采样也必须走完1000步,计算成本极高。
DDIM则提出了一种非马尔可夫的前向过程,从而允许训练好的模型大幅的去减少前向采样的步数。如果训练时用了1000步,前向采样只需要50步,计算成本大大降低。
DDIM的采样公式是对方程的精确解的一种离散化近似,其设计本身就考虑了大步长的情况。因此,即使在步数很少时,它也能生成非常清晰、连贯的图像,而DDPM在同等步数下会产生大量伪影和不连贯的结构。这一发现为扩散模型引入了ODE的数学概念,启发了后续一系列更高阶、更高效的ODE求解器(如DPM-Solver),进一步推动了采样速度的提升。可以说,DDIM是连接早期DDPM和现代快速扩散模型算法的关键桥梁。
三、LDM模型
High-Resolution Image Synthesis with Latent Diffusion Models论文地址
1、模型结构
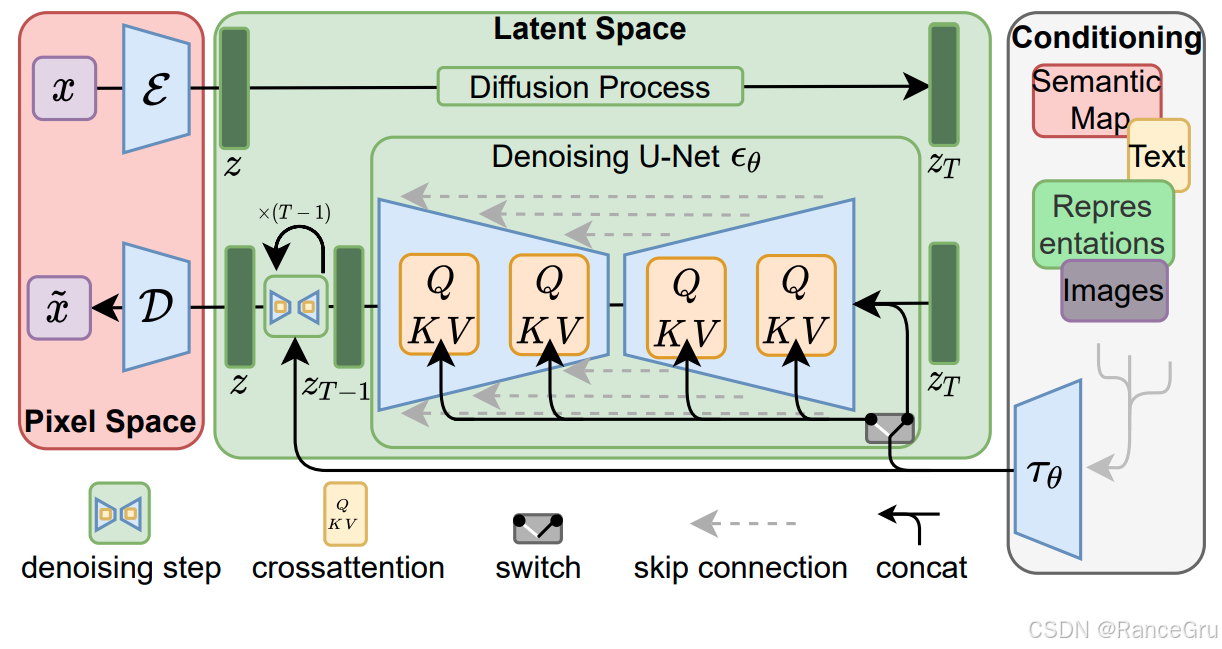
红色区域表示像素空间Pixel Space:
x
,
x
~
x,\tilde{x}
x,x~:输入输出的真实图像数据
ε \varepsilon ε:输入图像的编码器,将输入的真实图像压缩为一个维度小得多的潜在表示 z z z,可以理解为经过下采样的特征图,目的是去掉图像中的高频细节,保留了核心的语义信息。
D D D:输出图像的解码器,当潜在表示 z z z在潜在空间中完成去噪后,得到新的潜在表示 z ~ \tilde{z} z~后,通过解码器 D D D将 z ~ \tilde{z} z~重建回像素空间的最终高清图像 x ~ \tilde{x} x~。
绿色区域表示潜在空间Latent Space:
D
i
f
f
u
s
i
o
n
P
r
o
c
e
s
s
Diffusion\ Process
Diffusion Process:在低维空间中对潜在表示
z
z
z进行扩散加噪过程。
D e n o i s i n g U N e t ϵ θ Denoising\ UNet\ \epsilon_{\theta} Denoising UNet ϵθ:在低维空间中对潜在表示 z T z_T zT进行预测去噪过程。
d e n o i s i n g s t e p denoising\ step denoising step:在 z T z_T zT到 z T − 1 z_{T-1} zT−1期间的去噪步骤,每一步都经历一次UNet处理,从 z T z_T zT到 z z z需要迭代T步。
c r o s s a t t e n t i o n cross\ attention cross attention:表示交叉注意力机制,让去噪阶段能够受到外界的文本或其他输入对模型进行引导的关键机制。允许图像生成期间能关注文本描述中的特定词语。
s w i t c h switch switch:表示开关,使得模型能在无条件生成和有条件生成之间的自主切换。这是实现 Classifier-Free Guidance 技术的核心。
s k i p c o n n e c t i o n skip\ connection skip connection:表示跳跃连接,是UNet模型架构的中的一种设计,可以实现模型中的下采样和上采样之间的特征流动。
c o n c a t concat concat:表示拼接,将时间步信息与UNet中的特征图进行拼接,将两个或多个张量在某个维度上连接起来。
z , z T z,z_T z,zT:潜在向量表示 z z z和经过T步扩散加噪的潜在向量表示 z T z_T zT。
Q , K , V Q,K,V Q,K,V:表示UNet模型中的交叉注意力块。
白色区域表示调节空间Conditioning:
S
e
m
a
n
t
i
c
M
a
p
、
T
e
x
t
、
R
e
p
r
e
s
e
n
t
a
t
i
o
n
s
、
I
m
a
g
e
s
Semantic\ Map、Text、Representations、Images
Semantic Map、Text、Representations、Images:表示语义图、文本、表征、图像等形式的调节信号。
τ θ \tau_{\theta} τθ:表示条件编码器,用把编码调节信号编码成U-Net能够理解的统一特征向量。
2、公式原理
x
t
=
α
t
‾
∗
x
+
1
−
α
t
‾
∗
ϵ
x_t = \sqrt{\overline{\alpha_t}}\ast x+\sqrt{1-\overline{\alpha_t}}\ast \epsilon
xt=αt∗x+1−αt∗ϵ
L
D
M
=
E
x
,
ϵ
∗
N
(
0
,
1
)
,
t
[
∥
ϵ
−
ϵ
θ
(
x
t
,
t
)
∥
2
2
]
L_{DM} = \Bbb{E}_{x,\epsilon \ast N(0,1),t}[\parallel \epsilon-\epsilon_{\theta}(x_t,t)\parallel_2^2]
LDM=Ex,ϵ∗N(0,1),t[∥ϵ−ϵθ(xt,t)∥22]
以上两条公式分别是前向扩散公式和标准扩散模型的训练损失函数,其中:
L
L
L:表示扩散模型的损失值
E
\Bbb{E}
E:表示期望值,用于计算对多个变量的平均。
x
,
x
t
x,x_t
x,xt:表示图像数据
x
x
x与加噪图像数据
x
t
x_t
xt。
ϵ
,
ϵ
θ
\epsilon,\epsilon_{\theta}
ϵ,ϵθ:表示预测噪声和UNet去噪网络。
∥
⋅
∥
2
2
\parallel \cdot \parallel_2^2
∥⋅∥22:表示L2范数的平方,即MSE均方误差。
这两个函数源于去噪扩散概率模型DDPM,通过最小化预测噪声的误差来训练模型。
L
L
D
M
=
E
ε
(
x
)
,
ϵ
∗
N
(
0
,
1
)
,
t
[
∥
ϵ
−
ϵ
θ
(
z
t
,
t
)
∥
2
2
]
L_{LDM} = \Bbb{E}_{\varepsilon(x),\epsilon \ast N(0,1),t}[\parallel \epsilon-\epsilon_{\theta}(z_t,t)\parallel_2^2]
LLDM=Eε(x),ϵ∗N(0,1),t[∥ϵ−ϵθ(zt,t)∥22]
以上公式是无条件调节潜在扩散模型的训练损失函数,其中:
z
t
z_t
zt:表示潜在变量
z
z
z经过时间步t后得到的加噪图像,而
z
z
z是编码器对真实图像数据
x
x
x处理后得到的输出。
无条件调节LDM通过编码器在潜在空间中压缩数据,然后应用到扩散过程,提高扩散效率,常用于高分辨率图像生成。
L
L
D
M
=
E
ε
(
x
)
,
y
,
ϵ
∗
N
(
0
,
1
)
,
t
[
∥
ϵ
−
ϵ
θ
(
z
t
,
t
,
τ
θ
(
y
)
)
∥
2
2
]
L_{LDM} = \Bbb{E}_{\varepsilon(x),y,\epsilon \ast N(0,1),t}[\parallel \epsilon-\epsilon_{\theta}(z_t,t,\tau_{\theta}(y))\parallel_2^2]
LLDM=Eε(x),y,ϵ∗N(0,1),t[∥ϵ−ϵθ(zt,t,τθ(y))∥22]
以上公式是条件调节潜在扩散模型的训练损失函数,其中:
τ
θ
\tau_{\theta}
τθ:表示条件编码器,负责将条件
y
y
y映射为嵌入向量,比如CLIP或BERT等。
y
y
y:表示有条件输入,主要是以语义图、文本、表征、图像等形式数据作为输入。
条件调节LDM允许可控生成,可根据文本等内容生成图像,这些条件信息是通过交叉注意力机制集成到去噪网络中。
A
t
t
e
n
t
i
o
n
(
Q
,
K
,
V
)
=
s
o
f
t
m
a
x
(
Q
K
T
d
k
)
V
Attention(Q, K, V ) = softmax(\frac{QK^T}{\sqrt{d_k}})V
Attention(Q,K,V)=softmax(dkQKT)V
Q
=
W
Q
(
i
)
⋅
ϕ
i
(
z
t
)
,
K
=
W
K
(
i
)
⋅
τ
θ
(
y
)
,
V
=
W
V
(
i
)
⋅
τ
θ
(
y
)
Q = W_Q^{(i)}\cdot \phi_i(z_t), K = W_K^{(i)}\cdot \tau_{\theta}(y), V = W_V^{(i)}\cdot\tau_{\theta}(y)
Q=WQ(i)⋅ϕi(zt),K=WK(i)⋅τθ(y),V=WV(i)⋅τθ(y)
以上两条公式分别是标准注意力机制公式和条件注入QKV公式,其中:
Q
,
K
,
V
Q,K,V
Q,K,V:表示Q查询、K键、V值,属于输入矩阵,在LDM中分别来自潜在表示和条件编码。
W
W
W:表示可学习的投影矩阵,用于将输入映射到查询、键、值空间。
ϕ
i
\phi_i
ϕi:表示去噪网络UNet在第i层的中间特征。
τ
θ
\tau_{\theta}
τθ:表示条件编码器,负责将条件
y
y
y映射为嵌入向量,比如CLIP或BERT等。
z
t
z_t
zt:表示潜在变量
z
z
z经过时间步t后得到的加噪图像,而
z
z
z是编码器对真实图像数据
x
x
x处理后得到的输出。
y
y
y:表示有条件输入,主要是以语义图、文本、表征、图像等形式数据作为输入。
在去噪过程中,U-Net的每个空间位置Q根据与文本条件KV的相似度,自适应地加权融合文本信息,这使模型能生成与条件一致的高质量图像。
四、DiT模型
Scalable Diffusion Models with Transformers论文地址
1、Latent Diffusion Transformer
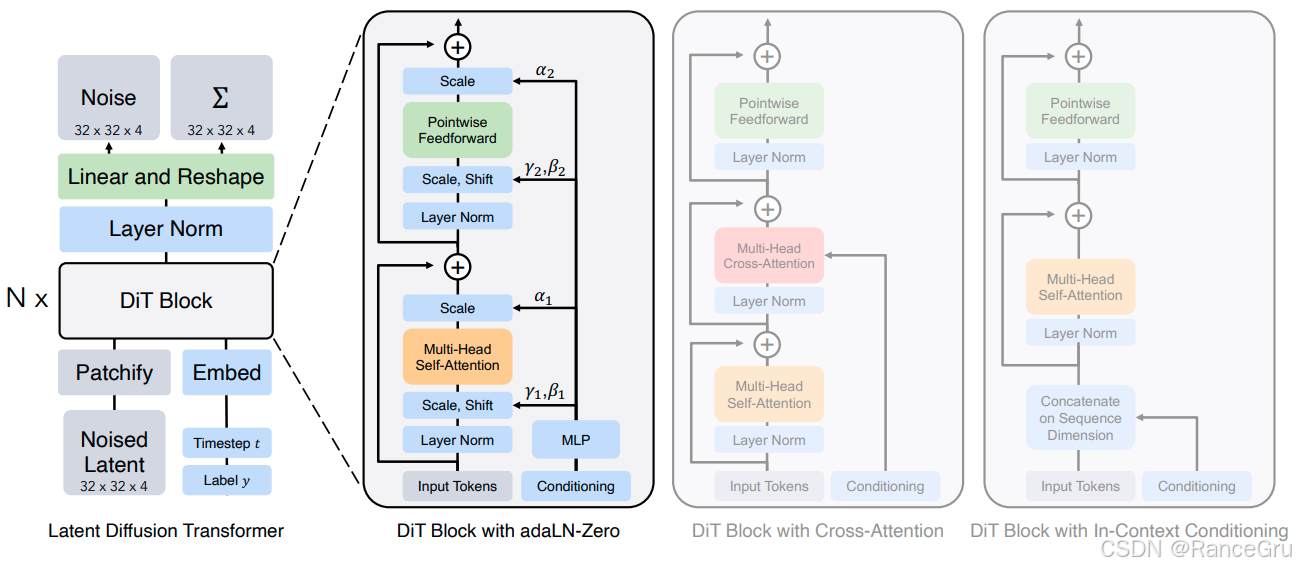
N o i s e d L a t e n t Noised\ Latent Noised Latent:表示带有不同程度噪声的潜在表示张量,将原始图片通过编码器压缩到潜在空间,然后按照时间步逐步加噪。其中潜在表示张量大小为宽高为32,通道深度为4。
P a t c h i f y Patchify Patchify:表示切割分块与位置编码操作,将二维的潜在表示张量数据切割成一系列小的数据块,并注入位置信息,告诉它每个图像块在原始图像中的坐标位置。最终将每个块展平成一个向量输入给后续的Transformer块。
L a b e l y Label\ y Label y:表示语义图、文本、表征、图像等形式的外部输入条件。
T i m e s t e p t Timestep\ t Timestep t:表示一个时间步标量,指明当前在扩散过程中所处的阶段与加噪情况。模型需要知道时间步来相应地执行去噪操作。
E m b e d Embed Embed:表示条件编码器,目的是将条件信息和时间步信息编码成一个向量表示。
D i T B l o c k DiT\ Block DiT Block:表示一个特殊的Transformer块,根据扩散模型的需求对Transformer做了特殊设计,能够融入潜在表示向量和条件表示向量以及时间步信息。
L a y e r N o r m Layer\ Norm Layer Norm:表示层归一化,NLP领域常用的归一化技术,主要对训练数据进行标准化,稳定训练过程。
L i n e a r a n d R e s h a p e Linear\ and\ Reshape Linear and Reshape:表示全连接层和矩阵转换操作,Linear操作是将每个图像块向量投影到一个更高维的特征空间中。Reshape操作是将处理完的所有数据按照矩阵的形状维度重新拼接起来。
N o i s e Noise Noise:表示模型预测的潜在表示张量 z t z_{t} zt到潜在表示张量 z t − 1 z_{t-1} zt−1时应该要被去除的噪声。
Σ \Sigma Σ:表示扩散模型前向过程的数学公式。
2、DiT Block
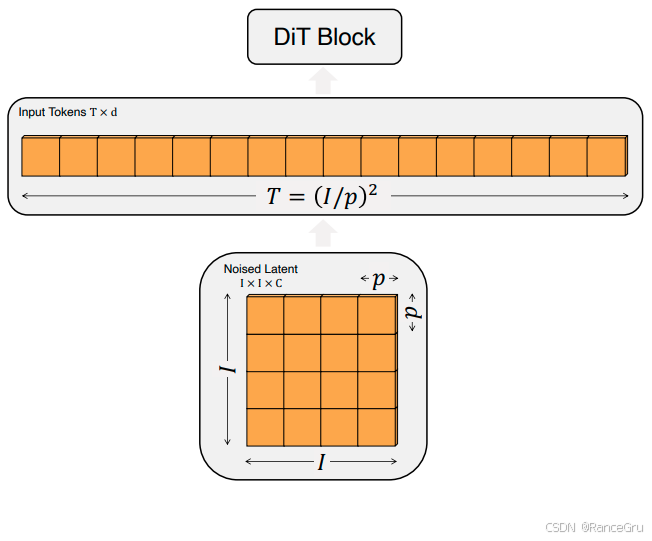
T T T:表示Token数量。
d d d:表示每个Token的维度。
I I I:表示原始噪声潜变量特征图的高度与宽度。
p p p:表示Patchify操作切分的每个Patch的高度与宽度。
C C C:表示原始噪声潜变量特征图的通道数。
通过Patchify操作将扩散模型的噪声潜变量特征图Noised Latent切分出T个Patch,然后转化为适合Transformer处理的Input Tokens序列,从而利用强大的 Transformer 架构来执行去噪任务。
3、DiT Block with adaLN-Zero
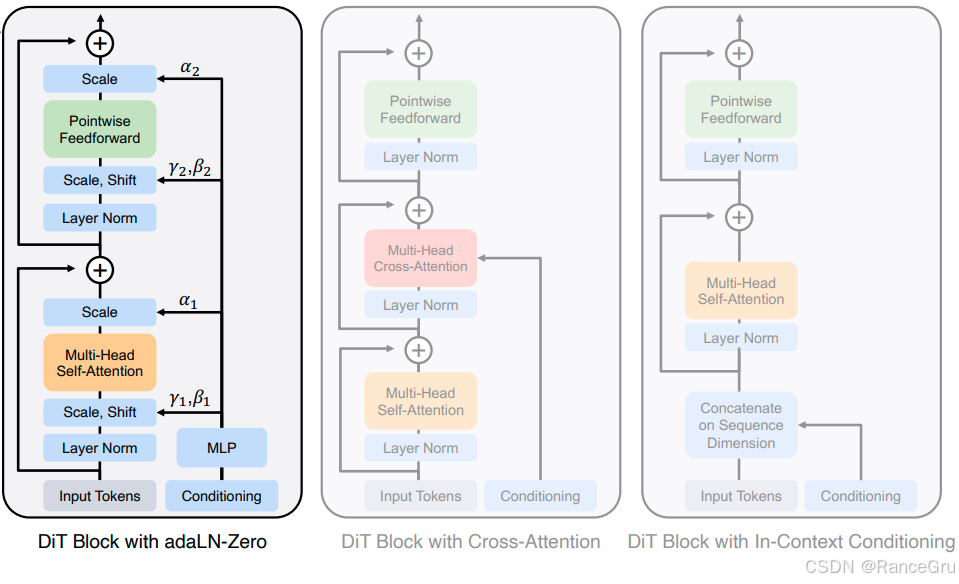
I n p u t T o k e n s Input Tokens InputTokens:表示被切分的潜在表示数据块,原始图像经过 N o i s e d L a t e n t Noised\ Latent Noised Latent和 P a t c h i f y Patchify Patchify处理后,被线性投影为一个Token,这些Token包含了被噪声破坏后的图像信息。
L a y e r N o r m Layer\ Norm Layer Norm:表示层归一化,NLP领域常用的归一化技术,主要对训练数据进行标准化,稳定训练过程。
C o n d i t i o n i n g Conditioning Conditioning:表示包含条件信息和时间步信息的向量数据,主要通过 L a b e l y Label\ y Label y、 T i m e s t e p t Timestep\ t Timestep t和 E m b e d Embed Embed操作把条件信息和时间步信息编码成了一个向量表示。
M L P MLP MLP:表示多层感知机,将带有条件信息和如时间步信息的条件向量编码映射成一组自适应参数。
S c a l e , S h i f t Scale, Shift Scale,Shift:表示缩放与平移操作,公式为 输出 = 输入 ∗ γ + β 输出 = 输入 * γ + β 输出=输入∗γ+β,也称为仿射变换,是深度学习中最基本的操作之一。
γ , β , α γ, β, α γ,β,α:表示根据不同的条件动态生成的 γ γ γ缩放因子、 β β β平移因子和 α α α残差权重,是由Conditioning和MLP计算得到的。其中 γ 1 , β 1 γ_1, β_1 γ1,β1被用于第一个Layer Norm之后,用于调节进入 多头自注意力模块 的数据。 γ 2 , β 2 γ_2, β_2 γ2,β2被用于第二个Layer Norm之后,用于调节进入 前馈网络模块 的数据。 α 1 , α 2 α_1, α_2 α1,α2在主路径中自注意力和前馈网络的输出与残差输入进行相加之前,对主路径的输出进行缩放。
M u l t i − H e a d S e l f − A t t e n t i o n Multi-Head Self-Attention Multi−HeadSelf−Attention:表示常规多头注意力机制。
P o i n t w i s e F e e d f o r w a r d Pointwise\ Feedforward Pointwise Feedforward:表示一个复杂非线性特征变换的模块,通常由一个简单的两层全连接网络构成,目的是对每个已经包含全局上下文信息的Token进行更深层次、更复杂的非线性特征变换。
a d a L N − Z e r o adaLN-Zero adaLN−Zero:是一种极其高效且稳定的条件注入机制,一方面将条件信息通过MLP映射得到 γ , β , α γ, β, α γ,β,α自适应参数,并使用缩放平移操作在注意力层和前馈层之前进行归一化操作,实现自适应归一化。另一方面将参数 α 1 , α 2 α₁, α₂ α1,α2初始化为 0。同时,也会将 γ 1 , γ 2 γ₁, γ₂ γ1,γ2初始化为接近0的值,使得模型可以学习在每个模块中如何按照条件信息进行更新,应该多大程度上依赖新计算的结果以及保留之前的信息。
优点:
高效简洁: 计算开销最小。只需要在块开始时从条件向量预测一组参数,之后的前向传播与标准Transformer块无异,没有引入额外的矩阵运算。
训练稳定: “Zero”初始化策略非常有效,能让模型平稳地从简单任务开始学习,避免了训练初期梯度爆炸或不稳定的问题。这是它性能强大的关键原因。
概念优雅: 将条件信息作为一种“调制”或“风格”信号,直接影响特征的均值和方差,与扩散模型生成时逐步“塑造”图像特征的过程非常契合。
缺点:
表达能力可能受限: 条件信息的影响是“间接”和“全局”的。它一次性调制了整个特征块,可能无法像Cross-Attention那样实现精细的、基于每个图像块(patch)和每个词汇(token)之间的交互。
灵活性较低: 对于需要非常精确的、细粒度的条件控制(例如,根据复杂的文本描述精确摆放物体位置),adaLN-Zero可能不如Cross-Attention直接。
4、DiT Block with Cross-Attention
DiT Block with Cross-Attention在Transformer块的自注意力(Self-Attention)层之后,插入一个交叉注意力(Cross-Attention) 层。
Query(Q): 来自图像的特征块(patches)。
Key(K)和 Value(V): 来自条件信息(如文本编码器的文本特征序列)。
通过计算Q和K的相似度,模型可以学会“关注”文本描述中与当前图像块最相关的部分,并用对应的V来更新图像特征。
优点:
强大的对齐能力: 这是其最核心的优势。它能够建立图像区域和文本词汇之间的显式、细粒度的关联。这对于实现“构图正确”的生成至关重要(例如,确保“一只戴帽子的猫”中的帽子在猫的头上,而不是其他地方)。
灵活性高: 天然适合处理序列形式的条件输入(如句子),可以捕捉条件中的复杂结构和依赖关系。
缺点:
计算开销大: 引入额外的注意力层会显著增加计算量和内存占用,尤其是当文本序列较长或图像分辨率很高时。
训练可能更困难: 需要学习两种不同的注意力机制(自注意力和交叉注意力),训练动态可能更复杂,有时需要更仔细的超参调优。
5、DiT Block with In-Context Conditioning
DiT Block with In-Context Conditioning不修改Transformer块的内在结构。相反,它将条件信息(如文本token)和图像信息(图像patch token)直接拼接在一起,形成一个更长的序列。
然后,将这个混合序列输入给一个标准的、只有自注意力(Self-Attention) 的Transformer块。
自注意力机制会自行学习图像块之间、文本token之间以及图像块与文本token之间的关系。
优点:
架构统一简洁: 无需为条件化设计特殊模块(如adaLN的预测网络或交叉注意力层)。模型就是一个标准的、仅有自注意力的Decoder-Only Transformer,简化了代码和系统设计。
潜力巨大: 这种方式让DiT更像一个“通用序列模型”,为多模态统一提供了可能。例如,可以很容易地将图像、文本、音频等不同模态的token一起输入模型进行训练,模型会自己学习它们之间的关联。这是通往“世界模型”的一种路径。
可扩展性: 受益于LLM领域在长序列处理上的持续进步。
缺点:
序列长度激增: 拼接会导致输入序列非常长(图像patch数量 + 文本token数量),而自注意力的计算复杂度是序列长度的平方(O(n²)),这在计算上是非常昂贵的,限制了其处理高分辨率图像的能力。
需要大量数据: 为了让模型有效地从这种“混杂”的输入中学习到正确的模态间交互关系,通常需要极其大规模的多模态数据进行预训练。
可能效率不高: 模型需要为每个样本都处理完整的混合序列,而adaLN-Zero和Cross-Attention中的条件信息(如文本嵌入)通常可以被预处理或共享,计算效率可能更高。
总结
UNet 凭借其独特的编码器-解码器结构以及跳跃连接,在图像分割任务中表现出色,能够有效保留细节信息。这一架构为后续生成模型奠定了基础。
DDPM 的核心创新在于其多步的扩散过程。它通过前向过程逐步向数据添加噪声,再通过反向过程学习从噪声中重建数据,其去噪网络通常基于UNet架构构建,从而能够生成质量较高的图像。
LDM 的关键改进在于计算效率的提升。它将DDPM中计算密集的像素空间扩散过程,转移至由VAE等编码器构成的低维潜空间中进行,大大降低了计算开销。同时,LDM通过交叉注意力机制巧妙地融入文本等条件信息,推动了可控文生图技术的发展。
DiT 用Transformer架构取代了LDM中的UNet。它将潜空间特征图切分为块(patch)作为输入序列,利用Transformer强大的全局建模能力和可扩展性,在图像生成质量上实现了新的突破,并为Sora等先进视频生成模型铺平了道路。
简而言之,这条技术路径从专用的分割网络UNet出发,经DDPM引入扩散思想,再由LDM优化计算效率并增强可控性,最终由DiT通过主流Transformer架构实现卓越的可扩展性,清晰地展现了生成模型在架构和能力上的持续进化。





















 1737
1737

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








