力扣85、最大矩形

难度：困难

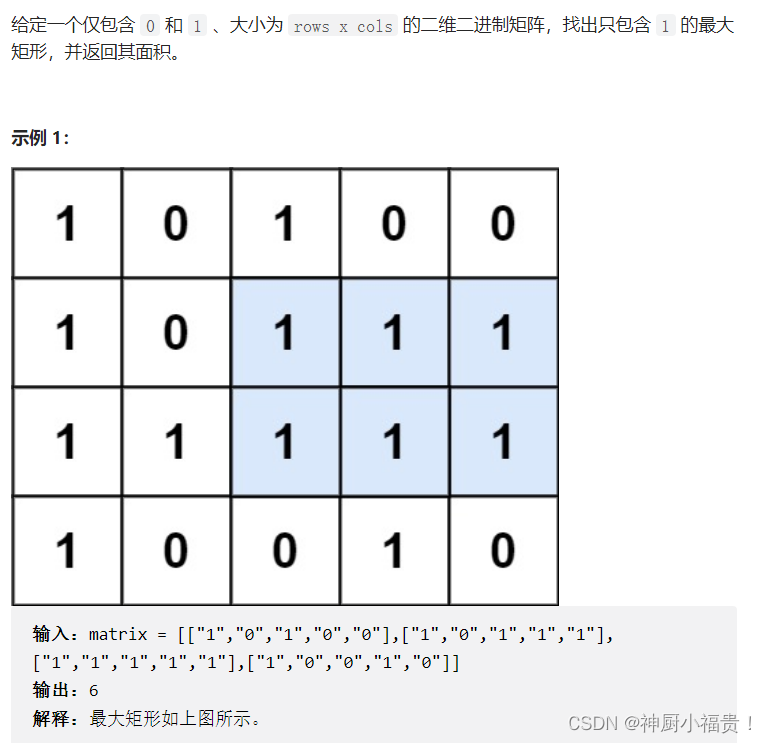
 该题思路为，将二维的数组转变为一维的，进行降维计算：

        定义一个heights[]数组来存储每一行中的数据，如果在这一行中遇到了matrix[i][j]为1的话，heights[j]++,否则的话，将heights[j]置为0。

        然后再将每一行的heights数组传入一个函数，对该行所形成的数组所组成的最大矩形进行一个保存到ans中，经过每一行的对比之后，经常max函数的筛选，就可以得到该二维数组中“1”所形成的矩形的最大值！

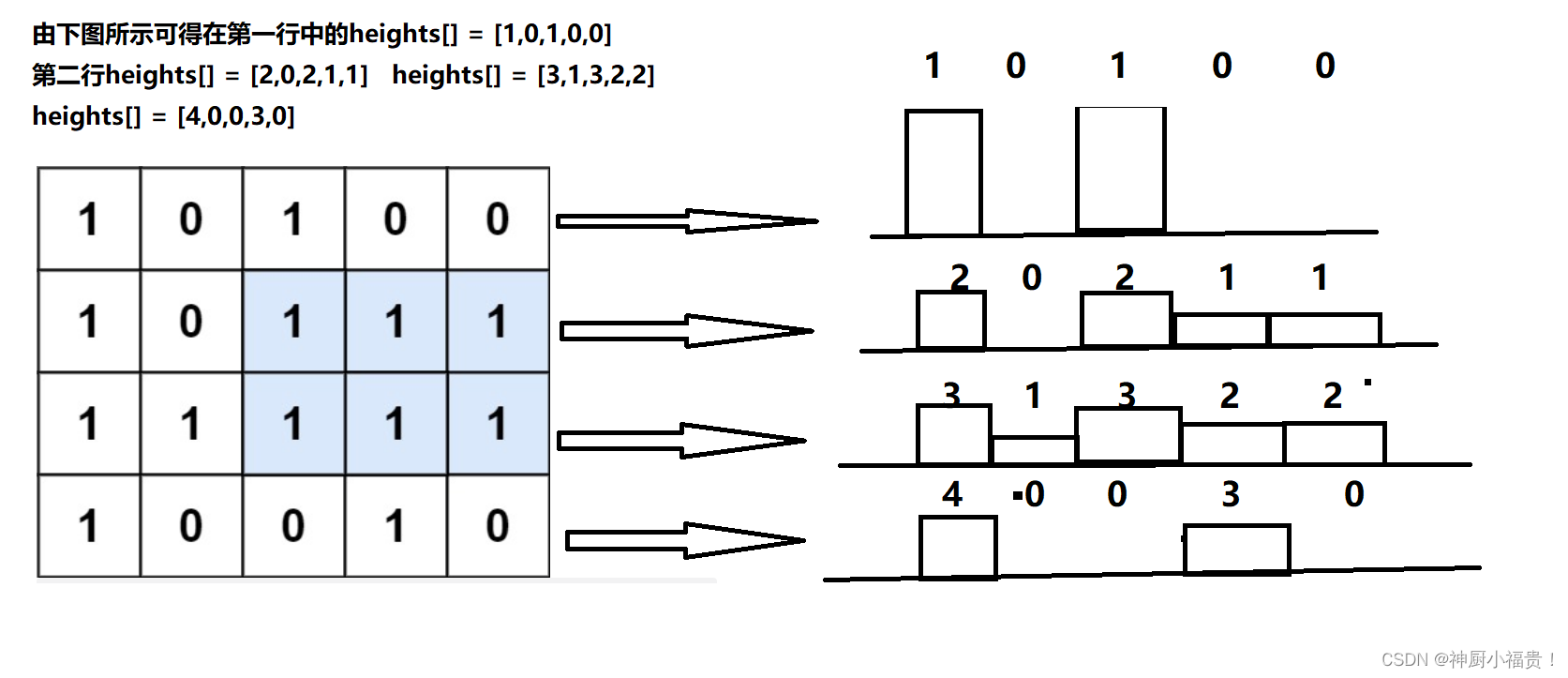
 如上图所示，那么这道题就变成了：力扣84、柱形图中最大的矩形

经过降维之后，就变得简单了：

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) 
    {
        int m = matrix.size();  //matrix行列
        int n = matrix[0].size(); 
        vector<int> heights(n);
        int ans = 0;
        for (int i = 0; i < m; ++i)
        {
            for (int j = 0; j < n; ++j)
            {
                if (matrix[i][j] == '1')
                {
                    heights[j]++;
                }
                else
                {
                    heights[j] = 0;
                }
            }
            ans = max(ans, maxArea(heights));   //将每一行遍历的结果传入maxArea函数中
        }
        return ans;
    }
    int maxArea(vector<int>& heights)
    {
        stack<int> stack;   //stack只保存下标i
        int ans = 0;
        heights.push_back(-1);  //保证heights的右边界
        for (int i = 0; i < heights.size(); ++i)
        {
            while (!stack.empty() && heights[stack.top()] > heights[i])
            {
                int idx = stack.top();
                stack.pop();
                int left = stack.empty() ? -1 : stack.top();
                ans = max(ans, (i - left - 1) * heights[idx]);
            }
            stack.push(i);
        }
        heights.pop_back();  //将heights末端插入的-1 pop出去
        return ans;
    }
};

思路取自于b站一位up主：【LeetCode 每日一题】85. 最大矩形 | 手写图解版思路 + 代码讲解_哔哩哔哩_bilibili