【C++】二叉树的先序、中序、后序遍历序列

二叉树常用到的遍历有这三种

先序遍历：先遍历根节点，然后再分别遍历左节点和右节点。(根左右)

中序遍历：先遍历左节点，然后再遍历根节点，最后遍历右节点。(左根右)

后序遍历：先遍历左节点，然后再遍历右节点，最后遍历根节点。（左右根）

如下图所示：

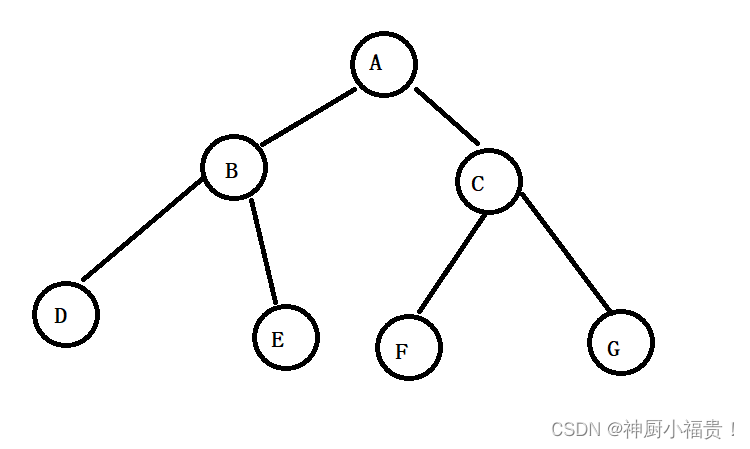
按照中序遍历的打印顺序为：D　B　E　A　F　C　G

按照先序遍历的打印顺序为：A　B　D　E　C　F　G

按照后序遍历的打印顺序为：D　E　B 　F 　G 　C 　A

我们先来看一下关于二叉树的创建:

先来看关于二叉树中指针的指向的创建:

typedef class BtNode
{
public:
	char data;  //数据
	struct BtNode* leftchild; //左孩子
	struct BtNode* rightchild;//右孩子
}BtNode, * BiaryTree;

二叉树的构建:

BtNode* CreatTree()
{
	BtNode* s = NULL;
	char elem;  //输入想进行中序,前序或后序遍历的二叉树节点
	cin >> elem;
	if (elem != '#')   //此处#代表孩子节点为NULL
	{
		s = BuyNode();
		s->data = elem;
		s->leftchild = CreatTree();
		s->rightchild = CreatTree();
	}
	return s;
}

二叉树创建中使用到的BuyNode()函数

BtNode* BuyNode()
{
	BtNode* s = (BtNode*)malloc(sizeof(BtNode));
	if (NULL == s) exit(1);
	memset(s, 0, sizeof(BtNode));
	return s;
}

实现上述三种遍历的代码:

递归版本的三种遍历方法

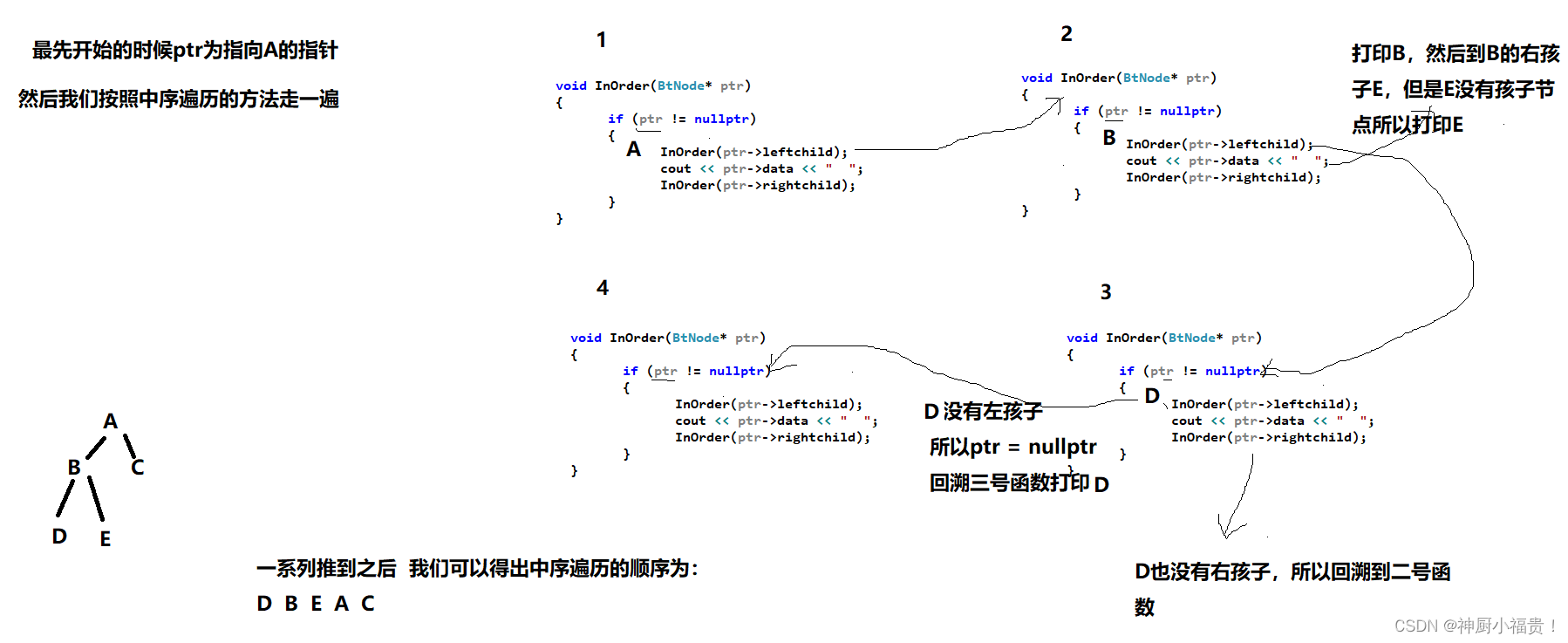
        递归实现中序遍历:

void InOrder(BtNode* ptr)
{
	if (ptr != nullptr)
	{
		InOrder(ptr->leftchild);
		cout << ptr->data << "  ";
		InOrder(ptr->rightchild);
	}
}

        递归实现前序遍历:

void PreOrder(BtNode* ptr)
{
	if (ptr != nullptr)
	{
		cout << ptr->data << "  ";
		PreOrder(ptr->leftchild);
		PreOrder(ptr->rightchild);
	}
}

        递归实现后续遍历:

void PassOrder(BtNode* ptr)   //
{
	if (ptr != nullptr)
	{
		PassOrder(ptr->leftchild);
		PassOrder(ptr->rightchild);
		cout << ptr->data << "   ";
	}
}

上述代码详解:(下图以中序遍历来举例,前序和后续类似)

 非递归版本的三种遍历:

中序遍历:

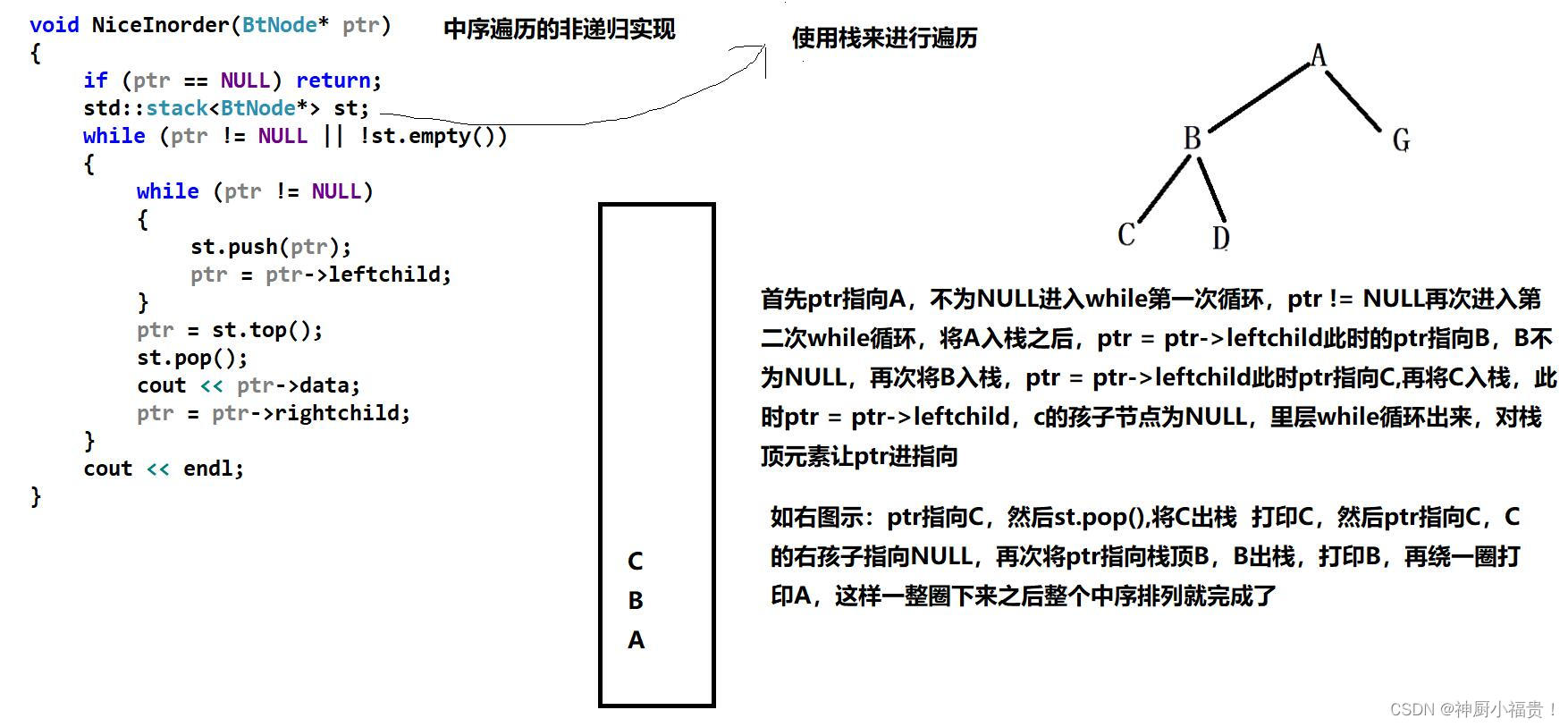
void NiceInorder(BtNode* ptr)
{
	if (ptr == NULL) return;
	std::stack<BtNode*> st;
	while (ptr != NULL || !st.empty())
	{
		while (ptr != NULL)
		{
			st.push(ptr);
			ptr = ptr->leftchild;
		}
		ptr = st.top(); 
		st.pop();
		cout << ptr->data;
		ptr = ptr->rightchild;
	}
	cout << endl;
}

后序遍历:

void NicepastOrder(BtNode* ptr)
{
	if (ptr == NULL) return;
	std::stack<BtNode*> st;
	BtNode* tag = NULL;   //tag指针相当于一个跟屁虫  你访问过那个指针 我就指向哪个指针
	while (ptr != NULL || !st.empty())   //剩下的思路和中序遍历几乎一毛一样
	{
		while (ptr != NULL)
		{
			st.push(ptr);
			ptr = ptr->leftchild;
		}
		ptr = st.top();
		st.pop();
		if (ptr->rightchild == NULL || ptr->rightchild == tag)
		{
			cout << ptr->data;
			tag = ptr;
			ptr = NULL;
		}
		else
		{
			st.push(ptr);
			ptr = ptr->rightchild;
		}
	}
	cout << endl;
}

非递归中序遍历的代码详解 (思路类似,对照着看,可以看明白的):

 

"多看多敲就可以变强(当然也可以变秃)"