Gradient Descent

---

在回归问题中，需要解决下面的最优化问题：

$${\theta }^{\ast }=\underset{\theta }{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}L(\theta )$$

• $L$ :lossfunction（损失函数）
• $\theta$ :parameters（参数）

L指损失函数，评判预测模型的性能，比如均方误差MSE，平方误差SE

$\theta$ 指代损失函数中的参数，比如线性回归中的 $w$ 和 $b$ 。

目的是要找一组参数 $\theta$ ，让损失函数（在training data上的值）越小越好，这个问题可以用梯度下降法解决：

假设$\theta$是参数的集合：Suppose that $\theta$ has two variables { θ 1 , θ 2 } \left\{\theta_{1}, \theta_{2}\right\} {θ1​,θ2​}

随机选取一组起始的参数：Randomly start at ${\theta }^0=\left[\begin{array}{l}{\theta }_1^0\\ {\theta }_2^0\end{array}\right]$

计算$\theta$处的梯度gradient：$\nabla L(\theta )=\left[\begin{array}{l}\partial L\left({\theta }_1\right)/\partial {\theta }_1\\ \partial L\left({\theta }_2\right)/\partial {\theta }_2\end{array}\right]$

$\left[\begin{array}{l}{\theta }_1^1\\ {\theta }_2^1\end{array}\right]=\left[\begin{array}{l}{\theta }_1^0\\ {\theta }_2^0\end{array}\right]-\eta \left[\begin{array}{l}\partial L\left({\theta }_1^0\right)/\partial {\theta }_1\\ \partial L\left({\theta }_2^0\right)/\partial {\theta }_2\end{array}\right]\Rightarrow {\theta }^1={\theta }^0-\eta \nabla L\left({\theta }^0\right)$

$\left[\begin{array}{c}{\theta }_1^2\\ {\theta }_2^2\end{array}\right]=\left[\begin{array}{c}{\theta }_1^1\\ {\theta }_2^1\end{array}\right]-\eta \left[\begin{array}{c}\partial L\left({\theta }_1^1\right)/\partial {\theta }_1\\ \partial L\left({\theta }_2^1\right)/\partial {\theta }_2\end{array}\right]\Rightarrow {\theta }^2={\theta }^1-\eta \nabla L\left({\theta }^1\right)$

---

梯度和学习率

参数 $\theta$的变化: ${\theta }^{n+1}={\theta }^n-\eta \nabla L({\theta }^n)$由两个因素组成一个是学习率$\eta$一个是梯度$\nabla L({\theta }^n)$；梯度主要决定梯度下降的方向，学习率决定在下降方向上走多长的路。
梯度

学习率

若学习率适合，会比较顺利地到达到损失函数的局部最小值，若学习率太小；虽然最后能够走到局部最小的地方，但是它可能会走得非常慢；若学习率太大，可能会在“山谷”的上振荡；若学习率非常大，使得loss穿过“山谷”到达太远的地方。

---

数学依据

泰勒表达式

$h(x)=\sum _{k=0}^{\infty }\frac{h^{(k)}(x_0)}{k!}(x-x_0{)}^k=h(x_0)+h^{\prime }(x_0)(x-x_0)+\frac{h^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+...$

$h(x_0+\Delta x)=\sum _{k=0}^{\infty }\frac{h^{(k)}(x_0)}{k!}(\Delta x{)}^k=h(x_0)+h^{\prime }(x_0)(\Delta x)+\frac{h^{\prime \prime }(x_0)}{2!}(\Delta x{)}^2+...$

一元函数：$x\to x_0$ , $h(x)=h(x_0)+h^{\prime }(x_0)(x-x_0)+o(x-x_0)$

二元函数：$x\to x_0$并且$y\to y_0$，$h(x,y)=h(x_0,y_0)+\frac{\partial h(x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial h(x_0,y_0)}{\partial y}(y-y_0)+o(x-x_0)+o(y-y_0)$

证明：梯度下降的参数变化会导致损失值下降

梯度下降的参数变化: ${\theta }^{n+1}={\theta }^n-\eta \nabla L({\theta }^n)$

$$\begin{gathered} L({\theta }^{n+1})=L({\theta }^n-\eta \nabla L({\theta }^n)) \\ =L({\theta }^n)+\nabla L({\theta }^n)(-\eta \nabla L({\theta }^n))+o(-\eta \nabla L({\theta }^n)) \\ =L({\theta }^n)-\eta (\nabla L({\theta }^n){)}^2+o(-\eta \nabla L({\theta }^n)) \end{gathered}$$

在$\eta \nabla L({\theta }^n))\to 0$的时候，$\eta (\nabla L({\theta }^n){)}^2>0$，$o(-\eta \nabla L({\theta }^n))$可忽略，最终使得$L({\theta }^{n+1})<L({\theta }^n)$。也就是说，在学习率和梯度的乘积$\eta \nabla L({\theta }^n)$趋于0时，梯度下降法使得损失值下降，更一般的说这个值在一定限度内会保证损失值下降。

---

适应性学习率

通常的梯度下降形式：
$${\theta }^{t+1}\leftarrow {\theta }^t-\eta g^t$$

• $g^t=\frac{\partial L({\theta }^t)}{\partial \theta }$
• $\eta$为初始设置的常数

简单的Adaptive Learning rate

简单的方法：随着次数的增加，逐渐降低学习率

$${\eta }^t=\frac{{\eta }^t}{\sqrt{t+1}}，t是迭代次数$$

• 初始，离局部最低点比较远，使用大一点的学习率
• 随着迭代增加，离局部最低点越近，因而减少学习率

AdaGrad

$${\theta }^{t+1}\leftarrow {\theta }^t-\frac{{\eta }^t}{{\sigma }^t}{g}^t$$

• $g^t=\frac{\partial L({\theta }^t)}{\partial \theta }$
• ${\eta }^t=\frac{{\eta }^t}{\sqrt{t+1}}$
• ${\sigma }^t=\sqrt{\frac{1}{1+t}\sum _{i=0}^t(g^i{)}^2}$，将此前所计算的所有梯度值取均方

化简后
$${\theta }^{t+1}={\theta }^t-\frac{\eta }{\sqrt{\sum _{i=0}^t(g^i{)}^2}}{g}^t$$

• $g^t=\frac{\partial L({\theta }^t)}{\partial \theta }$
• $\eta$为初始设置的常数

反差效果

Adagrad考虑的是当迭代越深入，则更新幅度越小，最终趋向于0；并且，使某次变动大的参数更加平滑，造成反差效果。

估测二次微分值，寻找最优参数更新

以二次函数$y=a{x}^2+bx+c$举例

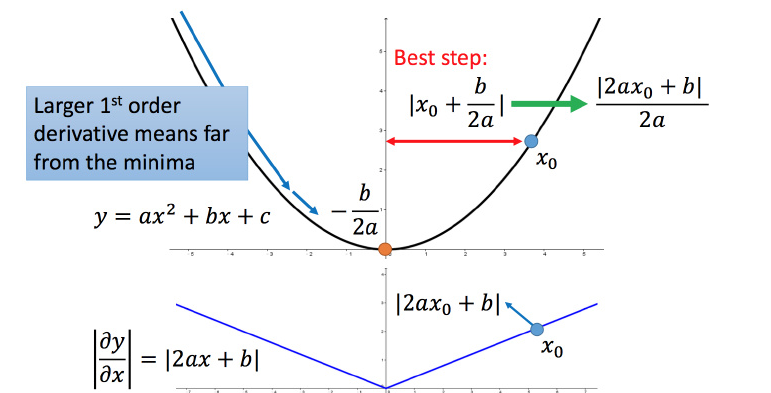
其最小值$x=-\frac{b}{2a}$，对于任意一点$x_0$，它迈出最好的步伐长度是$|x_0+\frac{b}{2a}|=|\frac{2a{x}_0+b}{2a}|$(直接迈到最小值点)，而该函数的一阶和二阶导数$y^{\prime }=2ax+b$、$y^{\prime \prime }=2a$，可以发现最好的一步是$|\frac{y^{\prime }}{y^{\prime \prime }}|$。

$g^t$是一次微分，$\sum _{i=0}^t(g^i{)}^2$近似于二次微分，直接计算二次微分的计算量较大，采用一次微分均方根的形式估测二次微分的值。模拟最优步伐。

Stochastic Gradicent Descent

普通的梯度损失函数：

$$L=\sum _n({\hat{y}}^n-(b+\sum {\theta }_i{x}_i^n){)}^2$$

随机梯度下降的损失函数：

$$L=({\hat{y}}^n-(b+\sum {\theta }_i{x}_i^n){)}^2$$

相同的梯度下降公式：

$${\theta }^i={\theta }^{i-1}-\eta ▽L({\theta }^{i-1})$$

普通梯度下降的损失函数需对所有数据的损失求平方和，后求取梯度，而随机梯度下降，只考虑一个数据，即可进行更新，更新速度跟快。

---

Feature Scaling

当多个属性的分布相差较大时，建议把他们的范围缩放，使得不同输入的范围是一样的。

方法

1. 对每一个维度（属性），求出平均值$m_i$，标准差${\sigma }_i$；
2. 对每一个数据的属性，相应减掉属性均值，除以属性标准差，即$x_i^r=\frac{x_i^r-m_i}{{\sigma }_i}$。

原理

考虑$y={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2$

• $x_1$的分布为100、200、300…
• $x_2$的分布为1、2、3…

当 ${\theta }_1$ 和 ${\theta }_2$ 做同样的变化时，${\theta }_1$ 对 $y$ 的变化影响是比较小的，${\theta }_2$ 对 $y$ 的变化影响是比较大的；不仅如此，我们的梯度下降可能由于步子大，越过“山谷”。